Street Race

Posted 2020-06-14

图一：有 10 个路口的街道

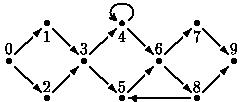
一个良好的跑道具有如下几个特点：

• 每一个路口都可以由起点到达。
• 从任意一个路口都可以到达终点。
• 终点不通往任何路口。

运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。

假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。（6不是 因为他所分成的两部分之间有公共街道8->6 so not ok）

怎么做呢？

感觉貌似又很恼火的样子。

但是数据范围并不大。直接模拟居然就well done。

1.枚举删除的点，判断是否起点终点还联通。（找出必经点）

2.同时看此必经点是否为中间点（因为中间点一定都是必经点，代码中有分析）

　怎么看呐。？就是把分成的两部分中一部分染色，另一部分看能否染成另一颜色且不重复咯。

　所以就是dfs + 标记什么的。

好的，思路就是这样了。详细分析在代码中。

代码:

/*
ID:Andy Chen
PROG: race3
LANG: C++
*/
#include <iostream>
#include <stdio.h>
#include <memory.h>
#include <vector>
using namespace std;
bool G[101][101];
int color[101];
vector<int> ans1;
vector<int> ans2;
bool dfs(int v,int m)//是否可以走到终点
//将此点标记也相当于将此点删除 
//删除后 如果起点走不到终点 说明这点就是必经点集中的一员了 
{
    color[v]=1;
    if(v==m)
        return true;
    for(int i=0;i<=m;i++)
    {
        if(G[v][i]&&!color[i])
        {
            if(dfs(i,m))
                return true;
        }
    }
    return false;
}
bool dfs2(int v,int m)//是否不会遇上以前搜过的点
//也就是用来判断是否符合题目要求2 ：此点是否为中间点
//1st    中间点一定是必经点 因为他把图分成两部分且互相独立
//可图本来是可以从起点到终点的
//2nd    怎么来判断？
//让dfs2 以此点为起点走之前未标记的那部分图
//如果能一直跑 不遇到color【】==1
//就说明  这点就是中间点了 
//因为他们已经完全分成两个部分了 
{
    if(color[v]==1)
        return false;
    color[v]=2;
    for(int i=0;i<=m;i++)
    {
        if(G[v][i]&&color[i]!=2&&!dfs2(i,m))
            return false;
    }
    return true;
}
int main()
{
    freopen("race3.in","r",stdin);
    freopen("race3.out","w",stdout);
    int a,b,m;
    m=0;
    memset(G,false,sizeof(G));
    for(int i=0;scanf("%d",&a)&&a!=-1;i++)
    {
        if(a==-2)
            continue;
        m=max(m,a);
        G[i][a]=true;
        for(int j=0;scanf("%d",&a)&&a!=-2;j++)
        {
            G[i][a]=true;
            m=max(m,a);
        }
    }//这貌似是笔者不怎么有没的神奇读入 
    for(int i=1;i<m;i++)
    {
        memset(color,0,sizeof(color));
        color[i]=1;
        if(!dfs(0,m))
        {
            ans1.push_back(i);
            color[i]=0;
            if(dfs2(i,m))
                ans2.push_back(i);
        }
    }
    cout<<ans1.size();
    for(int i=0;i<ans1.size();i++)
        cout<<‘ ‘<<ans1[i];
    cout<<endl;//必经点 
    cout<<ans2.size();
    for(int i=0;i<ans2.size();i++)
        cout<<‘ ‘<<ans2[i];
    cout<<endl;//中间点 
    return 0;
}