计算机程序的思维逻辑 (47) - 堆和PriorityQueue的应用

Posted 2020-08-17 老马说编程

本节介绍堆和PriorityQueue的两个应用，求前K个最大的元素，和求中值，相比排序，堆的效率更高，而且，还可以应对源源不断到来的动态数据，可以给出实时结果，那到底如何实现呢？

本系列文章经补充和完善，已修订整理成书《Java编程的逻辑》，由机械工业出版社华章分社出版，于2018年1月上市热销，读者好评如潮！各大网店和书店有售，欢迎购买，京东自营链接：http://item.jd.com/12299018.html

---

45节介绍了堆的概念和算法，上节介绍了Java中堆的实现类PriorityQueue，PriorityQueue除了用作优先级队列，还可以用来解决一些别的问题，45节提到了如下两个应用：

• 求前K个最大的元素，元素个数不确定，数据量可能很大，甚至源源不断到来，但需要知道到目前为止的最大的前K个元素。这个问题的变体有：求前K个最小的元素，求第K个最大的，求第K个最小的。
• 求中值元素，中值不是平均值，而是排序后中间那个元素的值，同样，数据量可能很大，甚至源源不断到来。 

本节，我们就来探讨如何解决这两个问题。

求前K个最大的元素

基本思路

一个简单的思路是排序，排序后取最大的K个就可以了，排序可以使用Arrays.sort()方法，效率为O(N*log2(N))。不过，如果K很小，比如是1，就是取最大值，对所有元素完全排序是毫无必要的。

另一个简单的思路是选择，循环选择K次，每次从剩下的元素中选择最大值，这个效率为O(N*K)，如果K的值大于log2(N)，这个就不如完全排序了。

不过，这两个思路都假定所有元素都是已知的，而不是动态添加的。如果元素个数不确定，且源源不断到来呢？

一个基本的思路是维护一个长度为K的数组，最前面的K个元素就是目前最大的K个元素，以后每来一个新元素的时候，都先找数组中的最小值，将新元素与最小值相比，如果小于最小值，则什么都不用变，如果大于最小值，则将最小值替换为新元素。

这有点类似于生活中的末尾淘汰，新元素与原来最末尾的比即可，要么不如最末尾，上不去，要么替掉原来的末尾。

这样，数组中维护的永远是最大的K个元素，而且不管源数据有多少，需要的内存开销是固定的，就是长度为K的数组。不过，每来一个元素，都需要找最小值，都需要进行K次比较，能不能减少比较次数呢？

解决方法是使用最小堆维护这K个元素，最小堆中，根即第一个元素永远都是最小的，新来的元素与根比就可以了，如果小于根，则堆不需要变化，否则用新元素替换根，然后向下调整堆即可，调整的效率为O(log2(K))，这样，总体的效率就是O(N*log2(K))，这个效率非常高，而且存储成本也很低。

使用最小堆之后，第K个最大的元素也很容易获得，它就是堆的根。

理解了思路，下面我们来看代码。

实现代码

我们来实现一个简单的TopK类，代码如下所示：

public class TopK <E> {
    private PriorityQueue<E> p;
    private int k;
    
    public TopK(int k){
        this.k = k;
        this.p = new PriorityQueue<>(k);
    }

    public void addAll(Collection<? extends E> c){
        for(E e : c){
            add(e);
        }
    }
    
    public void add(E e) {
        if(p.size()<k){
            p.add(e);
            return;
        }
        Comparable<? super E> head = (Comparable<? super E>)p.peek();
        if(head.compareTo(e)>0){
            //小于TopK中的最小值，不用变
            return;
        }
        //新元素替换掉原来的最小值成为Top K之一。
        p.poll();
        p.add(e);
    }
    
    public <T> T[] toArray(T[] a){
        return p.toArray(a);
    }

    public E getKth(){
        return p.peek();
    }
}    

我们稍微解释一下。

TopK内部使用一个优先级队列和k，构造方法接受一个参数k，使用PriorityQueue的默认构造方法，假定元素实现了Comparable接口。

add方法，实现向其中动态添加元素，如果元素个数小于k直接添加，否则与最小值比较，只在大于最小值的情况下添加，添加前，先删掉原来的最小值。addAll方法循环调用add方法。

toArray方法返回当前的最大的K个元素，getKth方法返回第K个最大的元素。

我们来看一下使用的例子：

TopK<Integer> top5 = new TopK<>(5);
top5.addAll(Arrays.asList(new Integer[]{
        100, 1, 2, 5, 6, 7, 34, 9, 3, 4, 5, 8, 23, 21, 90, 1, 0
}));

System.out.println(Arrays.toString(top5.toArray(new Integer[0])));
System.out.println(top5.getKth());

保留5个最大的元素，输出为：

[21, 23, 34, 100, 90]
21

代码比较简单，就不解释了。

求中值

基本思路

中值就排序后中间那个元素的值，如果元素个数为奇数，中值是没有歧义的，但如果是偶数，中值可能有不同的定义，可以为偏小的那个，也可以是偏大的那个，或者两者的平均值，或者任意一个，这里，我们假定任意一个都可以。

一个简单的思路是排序，排序后取中间那个值就可以了，排序可以使用Arrays.sort()方法，效率为O(N*log2(N))。

不过，这要求所有元素都是已知的，而不是动态添加的。如果元素源源不断到来，如何实时得到当前已经输入的元素序列的中位数？

可以使用两个堆，一个最大堆，一个最小堆，思路如下：

1. 假设当前的中位数为m，最大堆维护的是<=m的元素，最小堆维护的是>=m的元素，但两个堆都不包含m。
2. 当新的元素到达时，比如为e，将e与m进行比较，若e<=m，则将其加入到最大堆中，否则将其加入到最小堆中。
3. 第二步后，如果此时最小堆和最大堆的元素个数的差值>=2 ，则将m加入到元素个数少的堆中，然后从元素个数多的堆将根节点移除并赋值给m。

我们通过一个例子来解释下，比如输入元素依次为：

34, 90, 67, 45,1

输入第一个元素时，m即为34。

输入第二个元素时，90大于34，加入最小堆，中值不变，如下所示：

输入第三个元素时，67大于34，加入最小堆，但加入最小堆后，最小堆的元素个数为2，需调整中值和堆，现有中值34加入到最大堆中，最小堆的根67从最小堆中删除并赋值给m，如下图所示：

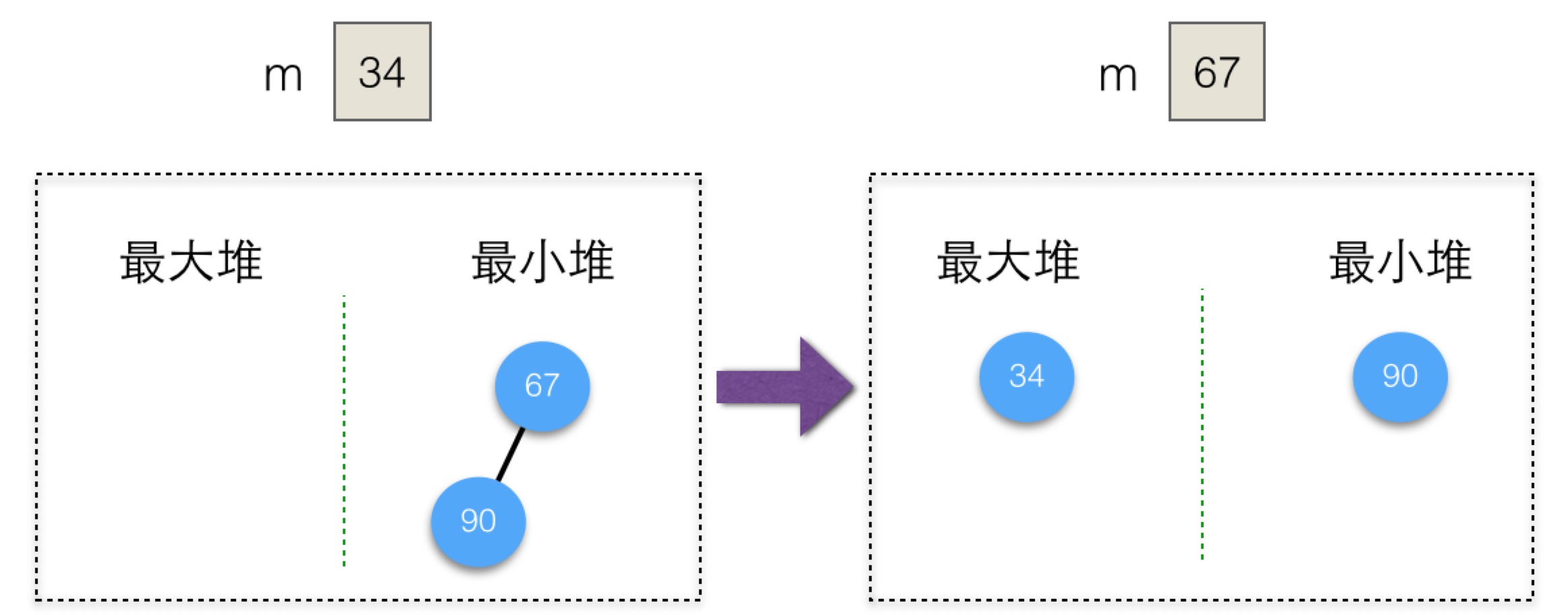
输入第四个元素45时，45小于67，加入最大堆，中值不变，如下图所示：

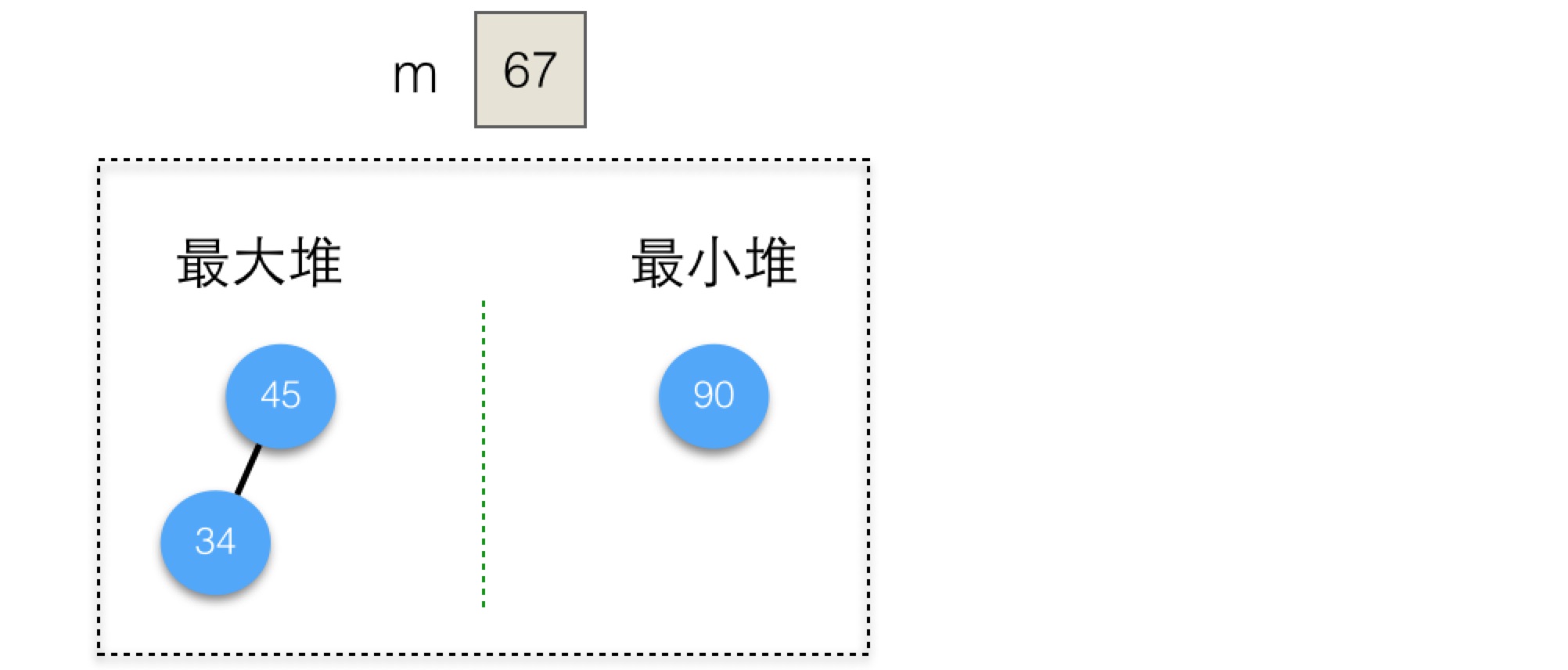
输入第五个元素1时，1小于67，加入最大堆，此时需调整中值和堆，现有中值67加入到最小堆中，最大堆的根45从最大堆中删除并赋值给m，如下图所示：

实现代码

理解了基本思路，我们来实现一个简单的中值类Median，代码如下所示：

public class Median <E> {
    private PriorityQueue<E> minP; // 最小堆
    private PriorityQueue<E> maxP; //最大堆
    private E m; //当前中值
    
    public Median(){
        this.minP = new PriorityQueue<>();
        this.maxP = new PriorityQueue<>(11, Collections.reverseOrder());
    }
    
    private int compare(E e, E m){
        Comparable<? super E> cmpr = (Comparable<? super E>)e;
        return cmpr.compareTo(m);
    }
    
    public void add(E e){
        if(m==null){ //第一个元素
            m = e;
            return;
        }
        if(compare(e, m)<=0){
            //小于中值, 加入最大堆
            maxP.add(e);
        }else{
            minP.add(e);
        }
        if(minP.size()-maxP.size()>=2){
            //最小堆元素个数多，即大于中值的数多
            //将m加入到最大堆中，然后将最小堆中的根移除赋给m
            maxP.add(this.m);
            this.m = minP.poll();
        }else if(maxP.size()-minP.size()>=2){
            minP.add(this.m);
            this.m = maxP.poll();
        }
    }
    
    public void addAll(Collection<? extends E> c){
        for(E e : c){
            add(e);
        }
    }
    
    public E getM() {
        return m;
    }
}

代码和思路基本是对应的，比较简单，就不解释了。我们来看一个使用的例子：

Median<Integer> median = new Median<>();
List<Integer> list = Arrays.asList(new Integer[]{
        34, 90, 67, 45, 1, 4, 5, 6, 7, 9, 10
});
median.addAll(list);
System.out.println(median.getM());

输出为中值9。

小结

本节介绍了堆和PriorityQueue的两个应用，求前K个最大的元素和求中值，介绍了基本思路和实现代码，相比使用排序，使用堆不仅实现效率更高，而且还可以应对数据量不确定且源源不断到来的情况，可以给出实时结果。

到目前为止，我们介绍了队列的两个实现，LinkedList和PriortiyQueue，Java容器类中还有一个队列的实现类ArrayDeque，它是基于数组实现的，我们知道，一般而言，因为需要移动元素，数组的插入和删除效率比较低，但ArrayDeque的效率却很高，甚至高于LinkedList，它是怎么实现的呢？让我们下节来探讨。

---------------

未完待续，查看最新文章，敬请关注微信公众号“老马说编程”(扫描下方二维码)，从入门到高级，深入浅出，老马和你一起探索Java编程及计算机技术的本质。用心原创，保留所有版权。