matlab 混沌，分形

Posted 2020-08-17

对于函数f(x)=λsin(πx)，λ∈(0,1]，使用matlab计算随着λ逐渐增大，迭代x=f(x)的值，代码如下：

function y=diedai(f,a,x1)

N=32;

y=zeros(N,1);

for i=1:1e4

    x2=f(a,x1);

    x1=x2;

    y(mod(i,N)+1)=x2;

end

end

 

%[email protected](a,x)a*x*(1-x);

[email protected](a,x)a*sin(pi*x);

%x0=0.1;

hold on;

for x0=-1:0.05:1

    for a=0:0.01:1

        y=diedai(f,a,x0);

        for count=1:32

            plot(a,y(count),‘k.‘);

            hold on;

        end

    end

end

 

 

得到的图像如下：其中横轴为λ，纵轴为x

 

 

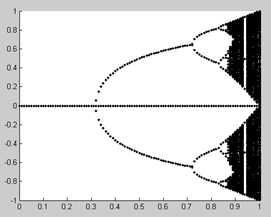
可以看到随着λ的逐渐增大，出现了倍周期分叉的情况。

由图中可以看出第一个分叉值大约在0.3附近，第二个在0.73到0.75之间，第三个在0.8到0.85之间，混沌大约出现在0.86附近。接下来编写代码计算分叉值，代码如下：

format long;

x0=0.1;

 for a=0.3182:0.0000001:0.3183

    y=diedai(f,a,x0);

    if max(y)>0.001

        disp(a);

        break;

    end

 end

 

得到第一个分叉值大约为0.3182298

 

format long;

x0=0.1;

 for a=0.7199:0.000001:0.72

    y=diedai(f,a,x0);

    if max(y)-min(y)>0.001

        disp(a);

        break;

    end

 end

 

得到第二个分叉值大约为0.719911

format long;

x0=0.1;

 for a=0.8332:0.000001:0.8333

    y=diedai(f,a,x0);

    if abs(y(32)-y(30))>0.001

        disp(a);

        break;

    end

 end

 

得到第三个分叉值大约为0.833267

 

利用Feigenbaum常数估计第三个分叉值，得到0.805939

 

分形图

周常青

画mandelbrot分形图，主要使用了三个函数：iter=mandelbrot1(x0,y0,maxIter)，用来计算迭代后是否收敛，方程z=z²+z0。c=color(iter,maxIter)计算颜色值，返回[r g b]。draw_mandelbrot1用来绘制图像。

function iter=mandelbrot1(x0,y0,maxIter)

x=x0;

y=y0;

    for i=1:1:maxIter

        if (x*x+y*y)>=4

            iter=i;

            break;

        else

            tem=x*x-y*y+x0;

            y=x*y*2+y0;

            x=tem;

        end

        iter=i;

    end

end

--------------------------------------------------------------------------------------------------------

function c=color(iter,maxIter)

    if iter==maxIter

        c=[1,0,0];

    else

        c1=abs(mod((iter*20+255),510)-255);

        c2=abs(mod((iter*15+85+255),510)-255);

        c3=abs(mod((iter*30+171+255),510)-255);

        c=[c1/255,c2/255,c3/255];

    end

end

-------------------------------------------------------------------------------------------------------

 

function  draw_mandelbrot1

for y=0:ymax

    for x=0:xmax

        xt=2*r*x/xmax+x0-r;

        yr=r*ymax/xmax;

        yt=2*yr*y/ymax+y0-yr;

        iter=mandelbrot1(xt,yt,maxIter);

        %c=color(iter,maxIter);

        c=color(iter,maxIter);

        plot(xt,yt,‘.‘,‘color‘,c);

        hold on;

      

    end

end

end

输入draw_mandelbrot1(-0.5,300,0,200,2,300)，得到的图像如下：

 

 

对收敛部分的颜色也进行绘制，画julia分形图，主要使用了三个函数[xList,yList,iter]=julia1(x0,y0,maxIter,jx0,jy0)，c=color2(iter,maxIter,xList,yList)，draw_julia1(x0,xmax ,y0,ymax, r,maxIter,jx0,jy0)。其中julia1使用方程z^’=z²+zm进行迭代，z0=x0+j*y0,zm=jx0+j*jy0;返回iter为迭代次数，color2根据不同的iter，和x，y值进行差值，计算出c=[r g b]，draw_julia1进行绘图。

 

在matlab里输入draw_julia1(0,300,0,200,1.6,50,-0.78888,0.212325)，得到如下图

 

 

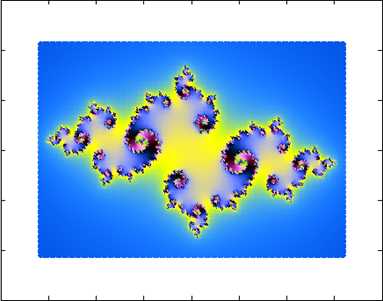
代码如下：

function [xList,yList,iter]=julia1(x0,y0,maxIter,jx0,jy0)

xList(1)=x0;

yList(1)=y0;

M=256;

lnln_m=log(abs(log(M)));

xbck=0;

ybck=0;

x=x0;

y=y0;

for i=1:maxIter

    if (x*x+y*y>=M)

%         iter=i;

        break;

    end

    xbck=x;

    ybck=y;

    tem=x*x-y*y+jx0;

    y=x*y*2+jy0;

    x=tem;

    xList(i+1)=x;

    yList(i+1)=y;

end

if i~=maxIter

    lnln_z=log(abs(log(x*x+y*y)));

    lnln_zbak=log(abs(log(xbck*xbck+ybck*ybck)));

    iter=i-2-(lnln_z-lnln_m)/(lnln_z-lnln_zbak);

else

    iter=i;

end

 

end

 

----------------------------------------------------------------------------------------------------

function c=color2(iter,maxIter,xList,yList)

% xList=xyList(1:length(xyList)/2);

% yList=xyList(length(xyList)/2:length(xyList));

[email protected](x)(sin(x*2*pi/510-pi*0.5)+1)*0.5*255;

 

if iter==maxIter

    x=xList(maxIter);

    y=yList(maxIter);

    z=sqrt(x*x+y*y);

    zd=z-sqrt(xList(maxIter-1)*xList(maxIter-1)+yList(maxIter-1)*yList(maxIter-1));

    r1=sincolorf(z*2000);

    g1=sincolorf(y*x*1000);

    b1=sincolorf(zd*1000);

%     errcolor(1)=errcolor(1)+r1;

%     errcolor(2)=errcolor(2)+g1;

%     errcolor(3)=errcolor(3)+b1;

else

    r1=sincolorf(iter*20);

    g1=sincolorf(iter*15+85);

    b1=sincolorf(iter*30+171);

%     errcolor(1)=errcolor(1)+r1;

%     errcolor(2)=errcolor(2)+g1;

%     errcolor(3)=errcolor(3)+b1;

end     

 

% result_r=fTcolor(errcolor(1));

% result_b=fTcolor(errcolor(2));

% result_g=fTcolor(errcolor(3));

 

r=r1/255;

g=g1/255;

b=b1/255;

 

c=[r g b];

end

 

-----------------------------------------------------------------------------------------------------------------------------

function draw_julia1(x0,xmax ,y0,ymax, r,maxIter,jx0,jy0)

for y=1:ymax

    for x=1:xmax

        xt=2*r*x/xmax+x0-r;

        yr=r*ymax/xmax;

        yt=2*yr*y/ymax+y0-yr;

        [xList,yList,iter]=julia1(xt,yt,maxIter,jx0,jy0);

%         xyList=[xList yList];

        c=color2(iter,maxIter,xList,yList);

        plot(xt,yt,‘.‘,‘color‘,c);

        hold on;

        %drawnow;

    end

end

end

 

可以看到，通过color2对收敛区域内部的颜色进行计算，可以得到色彩更为丰富的分形图，但是总体来说，因为对于相关知识的欠缺，比较难找到合适的颜色方案。