小谈剪枝研究

Posted 2023-03-16

参考技术A

本文主要从几篇论文以及几篇博客分享谈一下现在的剪枝发展，以及从自己的一些实践中实际剪枝的实验效果。

剪枝的理论基础就是过参数化（Over-parameterization）。在传统的机器学习中，过参数化意味着过拟合。

但是在深度学习中过参数化是不可或缺的。
（下面内容来自博客[Some intuition about over parameterization] https://zhuanlan.zhihu.com/p/40516287 )）

在深度学习中，从一个大的、过参数化的模型开始训练是有必要的，因为这样的模型具有很强的表示和优化能力。一旦训练完成到了推理阶段，我们并不需要这么多的参数。 这样的假设就支持我们可以在部署前对模型进行简化。模型压缩中的pruning和quantization两类方法正是基于这样的前提。

以下内容搬自 闲话模型压缩之网络剪枝（Network Pruning）篇 ）

剪枝的核心问题是成如何有效地裁剪模型且最小化精度的损失。
其实这不是一个新的问题，对于神经网络的pruning在上世纪80年代末，90年代初左右就有研究了。如论文《Comparing Biases for Minimal Network Construction with Back-Propagation》提出了magnitude-based的pruning方法，即对网络中每个hidden unit施加与其绝对值相关的weight decay来最小化hidden unit数量。又如上世纪90年代初当时经典的论文《Optimal brain damage》与《Second order derivatives for network pruning: Optimal Brain Surgeon》分别提出OBD和OBS方法，它们基于损失函数相对于权重的二阶导数（对权重向量来说即Hessian矩阵）来衡量网络中权重的重要程度，然后对其进行裁剪。但因为当时的大环境下，神经网络（那时没有deep neural network，只有neural network，或为区分称为shadow neural network）并不是机器学习的一个特别主流的分支，因此之后的很长一段时间也没有大量开枝散叶，但他们对问题的梳理定义和解决问题思路对二十多年后的很多工作产生了深远的影响。

到了2012年，我们都知道深度学习一战成名，大放异彩。
之后刷榜之风兴起且愈演愈烈，大家的注意力就是提高精度。于是大趋势就是不断地加深加重网络以提高精度，ImageNet准确率每年都创新高。
2015-16年期间，Hang Song等人发表了一系列对深度神经网络进行模型压缩的工作。如《Learning both weights and connections for efficient neural networks》，《EIE: Efficient inference engine on compressed deep neural network》。
其中《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding》获得了ICLR 2016的best paper。其中对当时经典网络AlexNet和VGG进行了压缩。结合pruning，quantization和huffman encoding等多种方法，将网络size压缩了几十倍，性能获得成倍的提升。其中对于pruning带来的精度损失，使用了iterative pruning方法进行补偿，可以让精度几乎没有损失。这让大家意识到DNN参数冗余程度如此之大，可榨油水如此之多。之后这几年，模型压缩领域变得越丰富，越来越多的相关工作衍生出各种玩法。

按照剪枝之后的结构是否依旧是对称的，剪枝可以分为 结构化剪枝和非结构化剪枝。

从剪枝的粒度上，可以分为：

剪枝主要是减掉不重要的参数，那么怎么衡量参数的重要性。这里对剪枝方法的分类主要来自于 闲话模型压缩之网络剪枝（Network Pruning）篇

一个最简单的启发就是按参数（或特征输出）绝对值大小来评估重要性，然后用贪心法将那部分干掉，这类称为magnitude-based weight pruning。
这种情况，往往需要参数是稀疏的，因此在训练时loss中加regularizer，尤其是L1 regularizer，从而使得权重稀疏化。对于structured pruning来说，我们想获得结构化的稀疏权重，因此常用group LASSO来得到结构化的稀疏权重。
为了剪枝掉参数较小的网络，可以 对卷积层 中的采纳数进行权重稀疏化，比如Learning Structured Sparsity in Deep Neural Networks》；可以 对BN层 的参数进行稀疏化训练，比如2017年的论文《Learning Efficient Convolutional Networks Through Network Slimming》；也可以对 激活函数 输出，像Relu这样的激活函数会倾向产生稀疏的activation，这样就可以减掉前面的通道层，比如2016年论文《Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures》。
这种方法有个假设就是参数绝对值越小，其对最终结果影响越小。我们称之为’‘smaller-norm-less-important’\'准则。然而这个假设未必成立（如2018年的论文《Rethinking the Smaller-Norm-Less-Informative Assumption in Channel Pruning of Convolution Layers》有对其的讨论）。

上世纪90年代初当时经典的论文《Optimal brain damage》与《Second order derivatives for network pruning: Optimal Brain Surgeon》分别提出OBD和OBS方法，它们基于损失函数相对于权重的二阶导数（对权重向量来说即Hessian矩阵）来衡量网络中权重的重要程度，然后对其进行裁剪。

这两种方法需要计算Hessian矩阵或其近似比较费时。近年来有一些基于该思路的方法被研究和提出。如2016年论文《Pruning Convolutional Neural Networks for Resource Efficient Transfer Learning》也是基于Taylor expansion，但采用的是目标函数相对于activation的展开式中一阶项的绝对值作为pruning的criteria。这样就避免了二阶项（即Hessian矩阵）的计算。2018年论文《SNIP: Single-shot Network Pruning based on Connection Sensitivity》将归一化的目标函数相对于参数的导数绝对值作为重要性的衡量指标。

对特征输出的可重建性的影响，即最小化裁剪后网络对于特征输出的重建误差。它的intuition是如果对当前层进行裁剪，然后如果它对后面输出还没啥影响，那说明裁掉的是不太重要的信息。典型的如2017年论文《ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression》和《Channel pruning for accelerating very deep neural networks》都是通过最小化特征重建误差（Feature reconstruction error）来确定哪些channel需要裁剪。

2019年的CV顶会CVPR上提出的一篇剪枝文章《Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration》这篇文章对较小范数不重要原则的进行重新审视。这个原则的基本要求是

因为大部分网络无法满足这个要求，因此提出了一个新的角度，如果一个filter可以被同一层的其他filters表征，那么说明这层是冗余的，即是可以被删除的。删除冗余层对整个层的影响是最小的，可以通过其他filters很快的恢复冗余层的信息。

那么什么样的filter是冗余层呢？什么层可以被同层的其他filters表征呢？
答案是 该层的几何中心或者说接近几何中心的filters 。在2008年的顶会CVPR的论文《Robust statistics on riemannian manifolds via the geometric median》提到了几何中心可以被几何中心附近的其他filters表征，这个理论奠定了这篇论文的理论基础。

剪枝比率是剪枝之后的参数占原始参数的比率。

剪枝可以分为静态剪枝和动态剪枝。

在传统的静态剪枝策略中，前人的研究发现从剪枝之后的网络结构重新初始化权重然后训练很难达到和剪枝前相同的精度。但是每次剪枝之后对保留的参数权重进行较少轮次的finetune的训练却可以使得相同的剪枝之后的网络结构达到或者只是略低于剪枝之前的精度。因此我们的共识是 剪枝之后留下的网络结构和网络参数的权重都很重要。
但是ICLR2019的best paper《The Lottery Ticket Hypothesis》首次提出了反对的意见。
这篇论文进行了这样的实验：

但是同年同会议的另一篇论文《Rethinking the Value of NetWork Pruning》给出了结论类似但又有些不同的观点。这篇论文同样否定了剪枝之后保留权重的重要性，但是也否定了保留初始化参数的必要性，认为 剪枝之后的finetune得到的模型效果，往往差于直接从头训练剪枝模型，虽然从头训练剪枝之后的结构的模型往往需要更多的训练轮次。

为什么之前的论文实验中，从头开始训练的实验效果都没有使用剪枝之后的参数的效果好？因为想当然的思想，使得之前的在“ 从头开始训练的”实验中没有仔细选择超参数、数据扩充策略，并且也没有给从头开始训练足够的计算时间和轮次（因为作者提到从头开始训练需要更多的轮次才能得到和利用剪枝参数进行finetune类似的精度）

《Rethinking the Value of NetWork Pruning》中的实验还有一个结论，就是 网络剪枝的作用就是网络结构搜索 。

作者针对《 Learning efficient convolutional networks through network slimming》这篇文章进行了5次随机从头训练，发现如果指定比率剪枝，那么5次剪枝之后，每层的保留层数总是神奇的相似，这说明这个方法确实可以得到一个比较高效稳定的结构。

关于预定义每层的剪枝比率以及根据训练结果动态计算剪枝比率两种方式，《Rethinking the Value of NetWork Pruning》给出的实验标明： 在VGG网络上，net-slimming剪枝策略优于每层等比例剪枝，而在ResNet,DenseNet上，net-slimming剪枝策略可能不如每层等比例剪枝。
作者分析了这些网络剪枝之后的结构，发现这种结构趋向于每层等比例剪枝，这可能就是这个策略剪枝之后的效果约等于每层等比例剪枝的原因。而VGG网络每层的冗余并不是均衡的，因此剪枝策略有效。

正如目前的研究所表明的

小谈 ArrayListList与数组

1、数组在初始化的时候要指定数组的大小，ArrayList本质也是数组，不过是一个动态的数组，大小是可以变化的

　　数组的大小：length；

　　ArrayList的大小：size。

2、数组很好理解，ArrayList是动态数组，究竟是怎么回事？我研究了一下

1 List<Integer> list = new ArrayList<>();
2 for(int i = 0;i< 37;i++) {
3 　　list.add(i);
4 }

View Code

 

　　对这段代码进行断点调试，然后观察List的变化：

　　list 刚初始化的时候，list本质是Object[0]，

　　

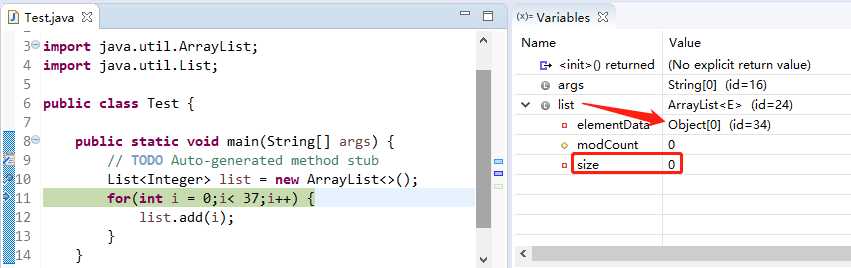
　　i ∈[0,9]，list本质是Object[10]，从list.add(0)的时候list由原本的Object[0]→Object[10]，

　　（注意看Object[0] id=34，而Object[10] id=39）

　　

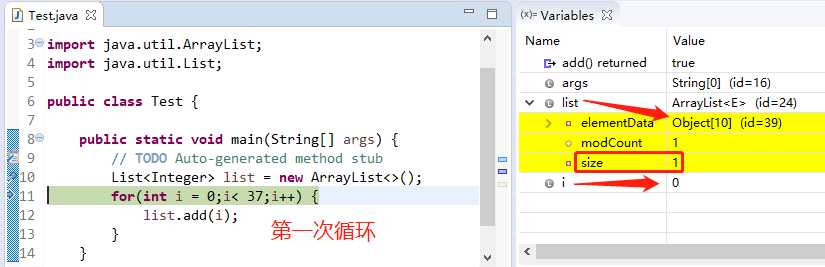
　　一直到第十次for循环，我们看到size在一次增加，而Object数组的length一直是10，没变。

　　（直到此时Object[10]  id=39，没有变化）

　　

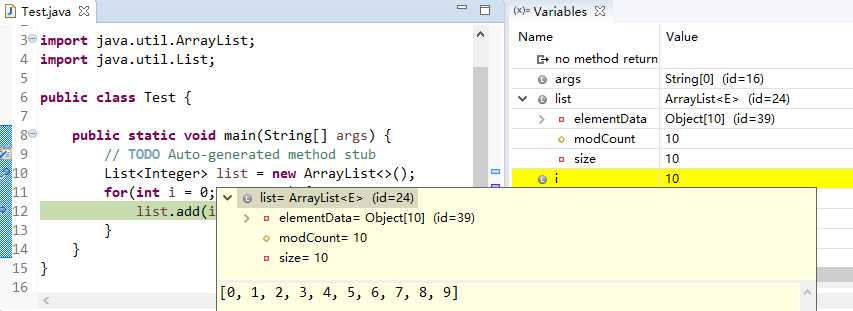
　　下面变化来了！当进入第11次循环体的时候，神奇的是Object数组的length变成了15！！！

　　（同时Object[15] id=62，变化了）

　　

　　

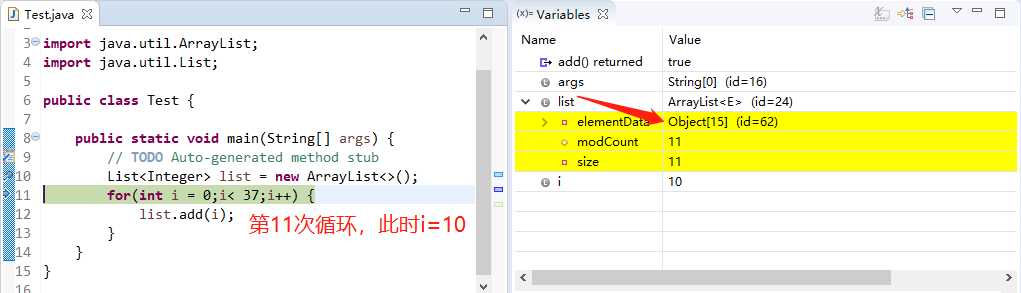
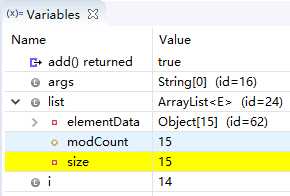
　　（直到第15次循环，Object[15] id=62  没变化，下面依次在Obiect[22]、Object[33]、Object[49]的时候id变化了）

　　

　　

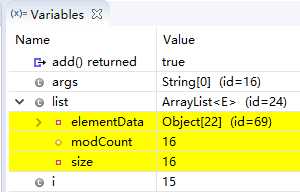
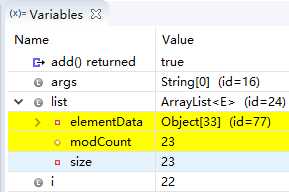
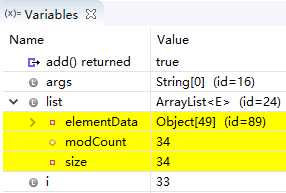
　　由上图的变化，可以看出ArrayList就是动态的数组，每当list真实的size达到Object的length的时候，又出来一个扩容、全新的Object数组（暂时不知，每一次扩容大小是什么规则），但至少满足用户需求。就这一点相较常规的数组来说，ArrayList更加灵活。

　　处女篇，欢迎指正~