数论之 HDU 2866

Posted 2020-08-16 fzfn5049

http://acm.hdu.edu.cn/showproblem.php?pid=2866

水题

题意：找 [2，L]内有多少个 p 满足 该式子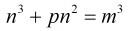，其中 n m 可以为任意整数，p为素数。

别人的gcd思路：

n^b + p*n^(b-1) = m^b   ==>   n^(b-1)*[n+p]=m^b

因为n里面要么有p因子，要么没有，所以gcd(n^(b-1),n+p)=1或(含有p因子的数)

当gcd(n^(b-1),n+p)== (含有p因子的数)的时候，显然无解，因为假设有解，那么n=K*p , K^(b-1)*p^b*(K+1)

如果希望上面的==m^b,那么K^(b-1) *(K+1)必须能表示成某个数X的b次方，而gcd(K,K+1)=1,所以他们根本就没共同因

子，所以没办法表示成X的b次方，所以gcd(n^(b-1),n+p)=1

 

假设n=x^b，n+p=y^b，那么显然m=x^(b-1)*y，而p=y^b-x^b

 

显然(y-x)|p，那么必须有y-x=1，所以y=x+1，代上去就发现，p=(x+1)^b-x ^b。所以枚举x,然后判断p是否是素数即可。

 

我的：n^3+pn^2=m  ==> n^2*(n+p)=m^b

然后先列举前几项 1^3+7*1^2=2^3  ==> 1^2*(1+7)=2^3

                         8^3+19*8^2=12^3   ==>  8^2*(8+19)=12^3

                         27^3+37*27^2=36^3  ==>  27^2*(27+37)=36^3 

                        ………………  

                  由此可见n+p=(i+1)^3  ,  所以 p肯定满足  p=(i+1)^3 - (i)^3    其中 i 为 [1,L] 中第几个数字temp满足该式子，又因为 p 为素数，所以只要找到 temp 这一数列中为素数的个数即可

 

 

 

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<algorithm>
 5 #include<iostream>
 6 using namespace std;
 7 int main(){
 8     long long p,i,ans,t,j;
 9     bool flag;
10     while(~scanf("%lld",&p)){
11             ans=0;
12             for(i=1;((i+1)*(i+1)*(i+1)-i*i*i)<=p;i++){
13                 t=(i+1)*(i+1)*(i+1)-i*i*i;
14                 flag=true;
15                 for(j=2;j*j<=t;j++){
16                     if(t%j==0){flag=false;break;}
17                 }
18                 if(flag==true)ans++;
19             }
20             if(!ans) printf("No Special Prime!\\n");
21             else cout<<ans<<endl;
22     }
23 }