Mayor's posters(离散化线段树)

Posted 2020-06-14

Mayor‘s posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 54067		Accepted: 15713

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
• The wall is divided into segments and the width of each segment is one byte. 
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.  Your task is to find the number of visible posters when all the posters are placed given the information about posters‘ size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 
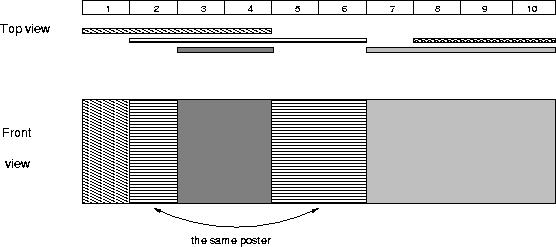
The picture below illustrates the case of the sample input. 

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4
题解：跟颜色段那道题很像，但是写了下wa，最后借助bin神的思路才写出来；

ac代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
#define mem(x,y) memset(x,y,sizeof(x))
#define SI(x) scanf("%d",&x)
#define PI(x) printf("%d",x)
#define SD(x,y) scanf("%lf%lf",&x,&y)
#define P_ printf(" ")
#define ll root<<1
#define rr root<<1|1
#define lson ll,l,mid
#define rson rr,mid+1,r
#define V(x) tree[x]
typedef long long LL;
const int MAXN=100010;
bool tree[MAXN<<2];
int h[10000010],seg[MAXN<<1];
struct Node{
	int a,b;
	Node init(int c,int d){
		a=c;b=d;
	}
};
Node dt[MAXN];
void build(int root,int l,int r){
	V(root)=false;
	int mid=(l+r)>>1;
	if(l==r)return;
	build(lson);build(rson);
}
bool query(int root,int l,int r,int A,int B){
	int mid=(l+r)>>1;
	if(V(root))return false;//线段树都是从上倒下访问的，覆盖的线段是true，就返回false 
	bool bcover;
	if(l==A&&r==B){
		V(root)=true;
		return true;
	}
	if(mid>=B)bcover=query(lson,A,B);
	else if(mid<A)bcover=query(rson,A,B);
	else{
		int b1=query(lson,A,mid);//
		int b2=query(rson,mid+1,B);//
		bcover=b1||b2;
	}
	if(V(ll)&&V(rr))V(root)=true;
	return bcover;
}
int main(){
	int T,N;
	SI(T);
	while(T--){
		SI(N);
		int a,b;
		int len=0,val=0;
		for(int i=0;i<N;i++){
			SI(a);SI(b);
			dt[i].init(a,b);
			seg[len++]=a;seg[len++]=b;
		}
		sort(seg,seg+len);
		int k=unique(seg,seg+len)-seg;
		for(int i=0;i<k;i++)h[seg[i]]=i;
		int ans=0;
		build(1,0,k-1);
		for(int i=N-1;i>=0;i--){//从上往下； 
			if(query(1,0,k-1,h[dt[i].a],h[dt[i].b]))ans++;
		}
		printf("%d\n",ans);
	}
	return 0;
}

　　wa代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
#define mem(x,y) memset(x,y,sizeof(x))
#define SI(x) scanf("%d",&x)
#define PI(x) printf("%d",x)
#define SD(x,y) scanf("%lf%lf",&x,&y)
#define P_ printf(" ")
#define ll root<<1
#define rr root<<1|1
#define lson ll,l,mid
#define rson rr,mid+1,r
#define V(x) tree[x]
typedef long long LL;
const int MAXN=20010;
int color[MAXN];
int temp;
int tree[MAXN<<2];
int seg[MAXN];
struct Node{
	int a,b;
	Node init(int c,int d){
		a=c;b=d;
	}
};
Node dt[MAXN];
void pushdown(int root){
	if(V(root)>0){
		V(ll)=V(root);
		V(rr)=V(root);
		V(root)=-1;
	}
}
void build(int root,int l,int r){
	int mid=(l+r)>>1;
	V(root)=0;
	if(l==r)return;
	build(lson);build(rson);
}
void update(int root,int l,int r,int A,int B,int v){
	if(l>=A&&r<=B){
		V(root)=v;
		return;
	}
	int mid=(l+r)>>1;
	pushdown(root);
	if(mid>=A)update(lson,A,B,v);
	if(mid<B)update(rson,A,B,v);
	V(root)=-1;
}
void query(int root,int l,int r){
	int mid=(l+r)>>1;
	if(temp==V(root))return;
	if(!V(root)){
		temp=0;return;
	}
	if(V(root)!=-1){
		if(temp!=V(root)){
			temp=V(root);
			color[temp]++;
			return;
		}
		return;
	}
	if(l==r)return;
		query(lson);
		query(rson);
}
int main(){
	int T,N;
	SI(T);
	while(T--){
		mem(color,0);
		SI(N);
		int a,b;
		int len=0;
		for(int i=0;i<N;i++){
			SI(a);SI(b);
			dt[i].init(a,b);
			seg[len++]=a;seg[len++]=b;
		}
		sort(seg,seg+len);
		int k=unique(seg,seg+len)-seg;
		build(1,1,k);
		for(int i=0;i<N;i++){
			a=lower_bound(seg,seg+k,dt[i].a)-seg;
			b=lower_bound(seg,seg+k,dt[i].b)-seg;
			update(1,1,k,a+1,b,i+1);
		}
		temp=0;
		query(1,1,k);
		int ans=0;
		for(int i=1;i<=N;i++){
			if(color[i])ans++;
		}
		printf("%d\n",ans);
	}
	return 0;
}