在AD和DA转换中的过采样和噪声形成

Posted 2020-08-16 告别年代

1. 直接量化的过采样AD转换

此类系统的模型可以用下图表示。

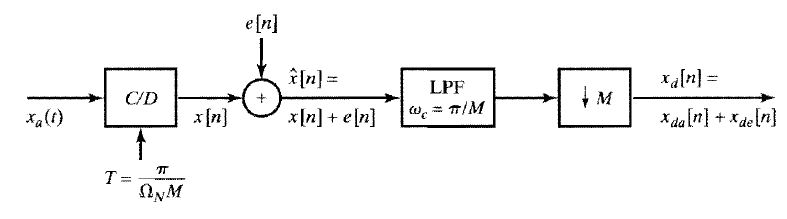
图中x_a(t)是输入信号，e(t)是量化引入的噪声，x_d[n]是最终得到的数字信号，包含分量x_da和x_de。

对于M倍过采样，信号与量化噪声的功率谱如下图。

从上图可以看出，M越大，信号与噪声之间的重叠部分就越少。

现在将上面的信号通过一个截止频率为PI/M的理想数字滤波器，信号功率不受影响，而PI/M之外的量化噪声将被滤除。再经过M倍降采样后，信号与量化噪声的功率谱就变成下面的样子（量化噪声只有滤波降采样前的1/M）：

计算表明（参考《离散时间信号处理》，奥本海默），为达到给定的信号量化噪声比，过采样率M每增加1倍，就可减少1/2位；或者说，为达到期望精度所能减少的位数N与过采样比M的关系为M=4^N。

 

2. 用噪声成形的过采样AD转换

前文述方法可以使用过采样的方法改善信噪比，但过采样比随着所需改善的位数提高而急剧增加。例如16b->20b，所需过采样比就是256。噪声成形的思路是将低频段的量化噪声“搬移”到高频部分去。如下图所示。

量化后的结果反馈回了输入端。

• D/A转换器：1个采样周期延时
• 积分器：离散时间电容积分器，使用累加器建模，y[n]=x[n]+y[n-1]，对应传递函数$H(z)=\\frac{1}{1-z^{-1} }$

于是这种方法的等效模型如下图：

 

从x[n]到y[n]的传递函数H_x(z)和从e[n]到y[n]的传递函数H_e[z]可以按系统叠加性质计算出来（分别置e[n]和x[n]为0）：

H_x(z)=1

H_e(z)=1-z^-1

它们的单位脉冲响应分别是

y_x[n]=x[n]

e\'[n]=e[n]-e[n-1]

这样，y[n]=x[n]+e\'[n]

e\'[n]可看做将e[n]通过一个单位冲击响应为δ[n]-δ[n-1]的系统而得到。对于LTI系统，输出功率谱是输入功率谱乘以系统频响函数的模平方，因此（设e[n]的功率谱为σ_e²）：

Φ_e\'e\'(e^jω)=σ_e²|H_e(e^jω)|²=σ_e²[2sin(ω/2)]²

与此对应的功率谱如下图。相比于直接过采样，噪声功率更多的位于PI/M之外。

有些文章将该系统对量化噪声的处理称作“滤波”，因为滑动差分的频率响应确实是高通。不过从滑动差分的频率响应来看，称之为“噪声形成”更合适一点。

以上所述即Delta-Sigma ADC的基本原理。这种方法可以进行级联，以进一步将量化噪声“推”到PI/M之外。

进一步的量化分析参考教科书。