清北第三套题
Posted 蒟蒻sjy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了清北第三套题相关的知识,希望对你有一定的参考价值。
铺瓷砖
(tile.cpp/c/pas)
【问题描述】
有一面很长很长的墙。 你需要在这面墙上贴上两行瓷砖。 你的手头有两种不同尺寸的瓷砖,你希望用这两种瓷砖各贴一行。瓷砖的长可以用分数表示,贴在第一行的每块瓷砖长度为 AB ,贴在第二行的每块瓷砖长度为CD 。本问题中你并不需要关心瓷砖的宽度。
如上图所示, 两排瓷砖从同一起始位置开始向右排列, 两排瓷砖的第一块的左端的缝隙是对齐的。你想要知道,最短铺多少距离后,两排瓷砖的缝隙会再一次对齐。
【输入】
输入的第 1 行包含一个正整数 T,表示测试数据的组数。
接下来 T 行,每行 4 个正整数 A,B,C,D,表示该组测试数据中,两种瓷砖的长度分别为 AB 和CD 。
【输出】
输出包含 T 行, 第 i 行包含一个分数或整数, 表示第 i 组数据的答案。 如果答案为分数,则以“X/Y”的格式输出,不含引号。分数必须化简为最简形式。如果答案为整数,则输出一个整数 X。
【输入输出样例 1】
tile.in tile.out
2
1 2 1 3
1 2 5 6
1
5/2
见选手目录下的 tile/tile1.in 与 tile/tile1.out
【输入输出样例 1 说明】
对于第一组数据,第一行瓷砖贴 2 块,第二行贴 3 块,总长度都为 1,即在距离起始位置长度为 1 的位置两行瓷砖的缝隙会再次对齐。
对于第二组数据,第一行瓷砖贴 5 块,第二行贴 3 块,总长度都为 52 。
【输入输出样例 2】
见选手目录下的 tile/tile2.in 与 tile/tile2.out
【数据规模与约定】
对于 50%的数据,1≤A,B,C,D≤20
对于 70%的数据,T≤10
对于 100%的数据,T≤100,000,1≤A,B,C,D≤10,000
题解:求出两个分母的最小公倍数即为答案。水。

#include<cstdio> #include<iostream> #include<algorithm> #define ll long long using namespace std; int T; ll fz1,fz2,fm; int a,b,c,d; ll gcd1(ll x, ll y)//最大公因数 { if (y==0) return x; ll k=x%y; gcd1(y,k); } int main() { freopen("tile.in","r",stdin); freopen("tile.out","w",stdout); scanf("%d",&T); while (T--) { scanf("%d%d%d%d",&a,&b,&c,&d); ll k1=gcd1(b,d); fm=b/k1*k1*(d/k1);//通分 fz1=fm/b*a; fz2=fm/d*c; k1=gcd1(fz1,fz2); ll fz=k1*(fz1/k1)*(fz2/k1);//化为最简整数比 if (fz%fm==0) cout<<fz/fm<<endl; else { k1=gcd1(fz,fm); fz/=k1;fm/=k1; cout<<fz<<\'/\'<<fm<<endl; } } fclose(stdin); fclose(stdout); return 0; }
小 Y 的问题
(question.cpp/c/pas)
【问题描述】
有个孩子叫小 Y,一天,小 Y 拿到了一个包含 n 个点和 n-1 条边的无向连通图,图中的点用 1~n 的整数编号。小 Y 突发奇想,想要数出图中有多少个“Y 字形”。一个“Y 字形”由 5 个不同的顶点 A、B、C、D、E 以及它们之间的 4 条边组成,其中 AB、BC、BD、DE 之间有边相连,如下图所示。同时,无向图中的每条边都是有一定长度的。一个“Y 字形”的长度定义为构成它的四条边的长度和。小 Y 也想知道,图中长度最大的“Y 字形”长度是多少。
【输入】
第一行包含一个整数 n,表示无向图的点数。
接下来 n 行,每行有 3 个整数 x、y、z,表示编号为 x 和 y 的点之间有一条长度为 z 的边。
【输出】
输出包含 2 行。
第 1 行包含一个整数,表示图中的“Y 字形”的数量。
第 2 行包含一个整数,表示图中长度最大的“Y 字形”的长度。
【输入输出样例 1】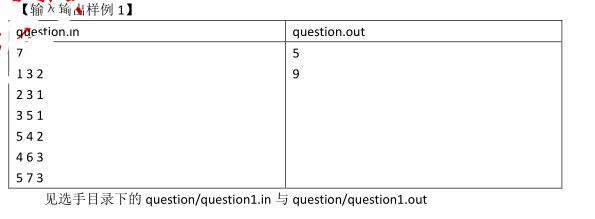
【输入输出样例 1 说明】
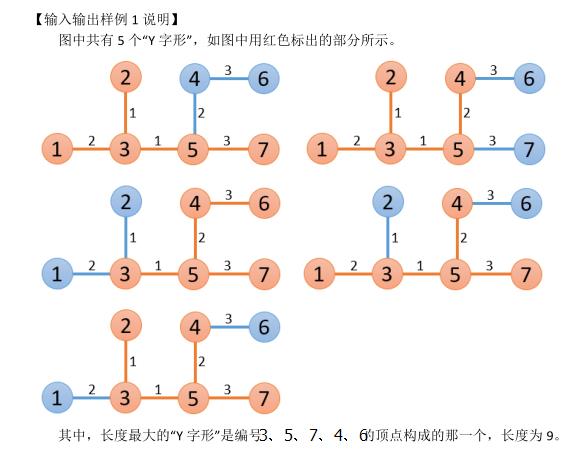
【输入输出样例 2】
见选手目录下的 question/question2.in 与 question/question2.out
【数据规模与约定】
对于 30%的数据,n≤10
对于 60%的数据,n≤2,000
对于 100%的数据,n≤200,000,1≤x,y≤n,1≤z≤10,000
考试时思路:观察图可以发现,所有满足条件的图,其中一定有一个点连着3个或三个以上的边,并且如果它的三条边连着的点还连着一条边的话,那么这5个点组成Y字形。因此记录下所有由3个和三个以上边的点。然后枚举找到答案。应该能得30分,不知道哪里出了点问题,只得了20分。

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define N 2010 #define ll long long using namespace std; int n,sum(0),ans1(0),ans2(0); int a[N][N],num[N]={0},w[N][N],f[N]; int main() { freopen("question.in","r",stdin); freopen("question.out","w",stdout); scanf("%d",&n); for (int i=1,x,y,z;i<n;i++) { scanf("%d%d%d",&x,&y,&z); a[x][++num[x]]=y; a[y][++num[y]]=x; w[x][num[x]]=w[y][num[y]]=z; if (num[x]>=3) f[++sum]=x; if (num[y]>=3) f[++sum]=y; } for (int i=1;i<=sum;i++) { int k=f[i]; int maxn=0; if (num[k]==3) { maxn=w[k][1]+w[k][2]+w[k][3]; for (int j=1;j<=3;j++) { int k1=a[k][j]; ans1+=num[k1]-1; for (int p=1;p<=num[k1];p++) { if (a[k1][p]!=k&&a[k1][p]!=a[k][1]&&a[k1][p]!=a[k][2]&&a[k1][p]!=a[k][3]) ans2=max(ans2,maxn+w[k1][p]); for (int q=1;q<=3;q++) if (a[k1][p]==a[k][q]) ans1--; } } } else { for (int j=1;j<num[k]-1;j++) for (int p=j+1;p<num[k];p++) for (int q=p+1;q<=num[k];q++) { maxn=w[k][j]+w[k][p]+w[k][q]; int k1=a[k][j]; ans1+=num[k1]-1; for (int l=1;l<=num[k1];l++) { if (a[k1][l]!=k&&a[k1][l]!=a[k][j]&&a[k1][l]!=a[k][p]&&a[k1][l]!=a[k][q]) ans2=max(ans2,maxn+w[k1][l]); if (a[k1][l]==a[k][j]) ans1--; if (a[k1][l]==a[k][p]) ans1--; if (a[k1][l]==a[k][q]) ans1--; } k1=a[k][p]; ans1+=num[k1]-1; for (int l=1;l<=num[k1];l++) { if (a[k1][l]!=k&&a[k1][l]!=a[k][j]&&a[k1][l]!=a[k][p]&&a[k1][l]!=a[k][q]) ans2=max(ans2,maxn+w[k1][l]); if (a[k1][l]==a[k][j]) ans1--; if (a[k1][l]==a[k][p]) ans1--; if (a[k1][l]==a[k][q]) ans1--; } k1=a[k][q]; ans1+=num[k1]-1; for (int l=1;l<=num[k1];l++) { if (a[k1][l]!=k&&a[k1][l]!=a[k][j]&&a[k1][l]!=a[k][p]&&a[k1][l]!=a[k][q]) ans2=max(ans2,maxn+w[k1][l]); if (a[k1][l]==a[k][j]) ans1--; if (a[k1][l]==a[k][p]) ans1--; if (a[k1][l]==a[k][q]) ans1--; } } } } cout<<ans1<<endl; cout<<ans2<<endl; fclose(stdin); fclose(stdout); return 0; }
以上是关于清北第三套题的主要内容,如果未能解决你的问题,请参考以下文章
