人工智能-遗传算法解决推箱子问题现实
Posted 晓风残月xj
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能-遗传算法解决推箱子问题现实相关的知识,希望对你有一定的参考价值。
原创作品,出自 “晓风残月xj” 博客,欢迎转载,转载时请务必注明出处(http://blog.csdn.net/xiaofengcanyuexj)。
由于各种原因,可能存在诸多不足,欢迎斧正!
一、研究背景
推箱子游戏中的路径查找问题—给定一方格,求两点最短距离。
传统求两点最短路径的算法有:
1.通用的搜索算法
2.解决无负权边的带权有向图的单源最短路问题的Dijkstra算法
3.求解含负权边的带权有向图的单源最短路径问题的Bellman-Ford算法
4.Bellman-ford算法改进版快速求解单源最短路经的Shortest Path Faster Algorithm
…
以上算法虽能百分之百找到最短路径,但是随着问题规模的扩大,随之而来的是组合爆炸问题,在有限的时间范围内难以求解问题。于是人们开始探索在有限时间内可以求得最优解的近似解。遗传算法求解两点最短路经就是在这样的背景下诞生的。
遗传算法是基于生物进化原理的一种全局性优化算法,是借鉴生物的自然选择和遗传进化机制而开发出的一种全局优化自适应概率搜索算法,是生物遗传技术和计算机技术结合的产物。它采用的是启发性知识的智能搜索算法,在高空问复杂问题上比以往有更好的结果。
本题大致就是求两点的最短路径,所不同的是我们没有给定问题的解空间,即在没有给定两点可达路径的基础上求两点的最短路径。可达路径基本可以经过遗传算法演化而来。
二、组内分工
| 成员名 | 身份 | 分工 |
| 徐进 | 组长 | 程序实现 |
| 熊凯平 | 组员 | 论文撰写 |
| 黄江 | 组员 | 算法设计 |
三、问题分析
给出n*m的二维方格,给定障碍物(数目及坐标),起点和终点,问绕过障碍物从起点到终点的最短路径。
基于题目,构建符合题意的模型。用户选择二维方格的行和列,即n和m。然后随机生成障碍物,为求合理真实,障碍物数目应控制在一定范围内,位置既不能太稀也不能太密,起点终点随机分布。我们的设计目标是尽可能不认为干预,让箱子自己跑。
在此说明,题目虽说是推箱子,但更我们玩的推箱子游戏是有所区别的。有图为证:
此图是实例给出的。不考虑推的方向,在此推箱子转化为路径查找问题。
四、算法设计
本题核心是求两点(绕过障碍的前提下)最短的哈夫曼距离。
一个很好地解决方案是BFS,时间复杂度为(n*m),空间复杂度接近常数。下面是BFS跑出的结果
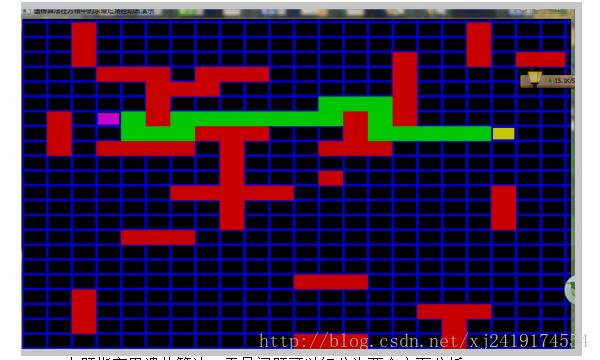
本题指定用遗传算法。于是问题可以细分为两个方面分析:
1.找到从起点到终点的路径
2.在所有的路径中找到尽可能短的。
在遗传算法中二者必须得到权衡。
本题没有用到高级的数据结构,用到了STL中的顺序容器Vector来存储每条染色体。然后开了些数组。
遗传算法 ( GA , Genetic Algorithm ) ,也称进化算法 。 遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
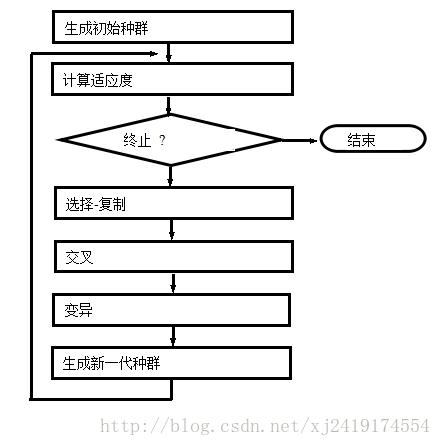
我们的遗传算法通用流程框图
种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ):一个遗传因子。
染色体 ( Chromosome ) :包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
五、算法实现
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。最简单的一种编码方式是二进制编码,即将问题的解编码成二进制位数组的形式。
§ 00 = up
§ 01 = right
§ 10 = down
§ 11 = left
每条染色体由只含0、1的偶数字符串组成,以上是4个基本基因片段。本题染色体是变长的(需考虑到具体题目),在不人为干预的情况下染色体所代表的运动方向是不确定的,这给问题的求解带来难度,如果染色体都过短则可能得不到路径;反之,如果染色体都过长,则可能得不到最短路径。我的方案是将染色体长度控制在[minlen,maxlen]之间,其中minlen为横坐标之差与纵坐标之差的和,maxlen为n*m-number(number为障碍物数目)。这样基本可以保证有染色体可以进化成最短路径。所有的遗传操作的基本单位都是2位0、1串。
适应度函数 ( Fitness Function ):用于评价种群中某个染色体的适应度,用Fitness(x)表示。本题及要找路径,还要找到最短的路径,即在从起点到目标点的可达路径都不知道的情况下的要筛选出最短的路径。这是本题面临的主要挑战。课件上给出的适应度函数如下:
Fitness[i] = 1 – (distance[i] / max possible distance)
其中distance[i]为染色体表示运动的终点与目标点的哈夫曼距离(在不可以障碍物的情况下)。这样的适应度函数如果不做修改时很可能陷入局部最优的。如图:
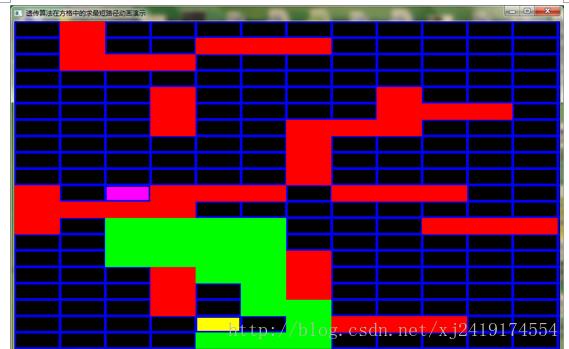
上图种群很可能找不到最优解。因为要找到最短的可达路径必须绕过去,而在绕的过程中经过上述适应度函数计算出来的适应值是很大程度上减小的。
我的解决方案是将distance[i]修改为BetDis[x][y],BetDis[x][y]表示(x,y)与目标点的考虑障碍物的最短距离。从而可以有效避免上述原因造成的过早陷入局部最优解。关于BetDis[x][y]可以通过预处理求得。通过一次BFS可以求得方格中所有点到目标点的最短距离,时间复杂度为O(n*m),空间复杂度也很低。
上述适应度度函数只能保证尽可能接近目标点,不能同时得到较短的路径。我们做了一些尝试,已知最短路径应该与目标的接近程度成正比,与路径长度成反比。我尝试将适应度函数修改为
NewFitness[i] = a*Fitness[i]+b/len;
或 NewFitness[i] = a*Fitness[i]/len;
其中a,b为待定常数,len为染色体Chro[i]的长度。
但最终没有找到比较合适的a,b。
于是我们还是选择了 Fitness[i] = 1 – (BetDis[x][y]/ max possible distance) 作为适应度函数。我们通过修正染色体来权衡二者。由于每条染色体都要求适应度,一个想法是在求适应度的过程中完成染色体的修正。我的修正方案有两个:
1.若某染色体Chro[i]在运动过程中经过目标节点,则直接将Fitness[i]置为1,同时截断后面的基因片段,即缩短染色体。如:
01 10 10 01 01 00 11 00 10 10 01 10 11 11 11 00 00 10 01
前8个基因片段就到达目标点,则后面的都是有害的,于是截断,修正染色体为
01 10 10 01 01 00 11 00
看似不符自然规律,但却给解题带来极大的优化。
2.若某染色体Chro[i]在运动过程中遇到不合法状态,即走到障碍物上或越出方格,则要修正相应的基因片段,我们采用不回溯法。若当前状态不合法,则转入下一个状态,
Direction=(Direction+1)%4,其中Direction取值为0,1,2,3。
Direction=0,对应基因片段00
Direction=1,对应基因片段01
Direction=2,对应基因片段10
Direction=3,对应基因片段11
这样的修正方法导致染色体是可以回走的。回溯法可以避免回走,但一个长度为Size的染色体最坏的时间复杂度为O(3^size),即当前染色体所走的每一步都要回溯,这样的时间复杂度是难以接受的。所以我们选择了不回溯的。如果繁衍代数足够多,在大量交叉、变异的前提下可以降低回走的影响。
遗传算法有3个最基本的操作:选择,交叉,变异。
选择:选择适应度高的染色体个体存活下来,淘汰适应度地的染色体个体。常用的选择策略是 “比例选择”,也就是个体被选中存活的概率与其适应度函数值成正比。假设群体的个体总数是PopulationSize,那么那么一个体Chro[i]被选中存活的概率为Fitness(Chro[i])/( Chro[0]+ Chro[1] + …….. + Chro[PopulationSize-1] ) 。比例选择算法可以通过“轮盘赌算法”( Roulette Wheel Selection ) 实现。关于轮盘赌算法的实现在这就不多说了。
为了防止进化过程中产生的最优解被交叉或变异所破坏,可以将每一代中的最优解原封不动的复制到下一代中,即我们采用了精英主义(Elitist Strategy)选择,这是我们采用的一种优化方案。
交叉(Crossover):基因交叉,就是把两个父体部分结构加以替换,生成新的个体的操作,本题的交叉操作比较简单,就是随机选择选择长度相同的染色体进行交叉,我们交叉的起始位置随机。如:
交叉前:
父辈1: 01 10 10 01 00 00 10 11 01 01 10 10 00 00 11 11 00 01
父辈2: 01 10 00 01 10 11 10 00 01 10 10 10 00 10 11 01 01 11
交叉后
子辈1: 01 10 10 01 00 11 10 00 01 01 10 10 00 00 11 11 00 01
子辈2: 01 10 00 01 10 00 10 11 01 10 10 10 00 10 11 01 01 11
所有交叉都是在交叉率CrossoverRate的控制下进行的,通过交叉率计算出当前种群的交叉数CrossoverNum。
While(交叉数CrossoverNum--)
{
随机选择等长的两条染色体;
随机选择起始位置进行交叉;
}
为了使程序效率不致太低,我们在交叉过程中并没有防止含非法状态的染色体产生,而是在求适应度的同时修正染色体。
变异(Mutation):在基因交叉之后产生的子代染色体个体中,有一部分个体的某个基因片段以很小的概率发生转变,这个过程称为变异(Mutation)。我们的变异操作也变较简单,随机选择染色体,随机选择染色体变异位置,随机选择变异方向,这样可以保证过早陷入局部最优解,因为假设种群没有最优解所必需的某个基因,而选择、交叉操作不产生新基因,只有通过变异完成。如:
变异前:10 01 01 01 10 10 11 01 11 00 11 11 11 00 11 00 10 10 01
变异后: 10 01 11 01 10 10 11 01 11 00 11 11 11 00 11 00 10 10 01
所有变异都是在变异率MutationRate的控制下进行的,通过变异率计算出当前种群的变异数MutationNum。
While(变异数MutationNum--)
{
随机选择某个染色体在随机位置向随机方向变异;
}
同交叉操作,为了使程序效率不致太低,我们在变异过程中并没有防止含非法状态的染色体产生,而是在求适应度的同时修正染色体。
六、算法实现伪代码
遗传算法伪代码GeneticAlgorithm
{
while(当前繁衍代数小于设定的繁衍代数)
{
当前繁衍代数加1;
进行选择操作Selection();
进行交叉操作Crossover();
进行变异操作Mutation();
}
}
算法的时间复杂度为O(Generation*popsize^2),在算法时间复杂度的计算过程中除去可视化时窗口延迟刷新的时间损耗;空间复杂度为O(n).
七、程序运行结果



八、参考论文
九.源程序
BFS算法实现
#include<iostream>
#include<windows.h>
#include<cstdio>
#include<string>
#include<queue>
#include<ctime>
#include<gl/glut.h>
using namespace std;
const int MAXNGRID=1000;//设置方格的总数
const int MAXN=50;//设置最大长、宽
int winHeight,winWidth;//当前窗口的长宽
bool MyLoop,SetRow,SetColumn,IsRun,First;//几个开关变量控制鼠标响应
int GridLen[2][10]=
{
{4,6,8,10,12,14,16,18,20,22},
{4,6,8,10,12,14,16,18,20,22}
};
int Move[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
struct state
{
int x,y;
string path;
}Start,Target;
queue<state>Qu;
struct point
{
int x,y;
};//建立方格的坐标(规则同OpenGL),便于投影到视区
class grid
{
private :
int Row,Column;
int TotalPointNumber,UsedPointNumber;
string OptimalPath;
point Point[MAXNGRID];
double RowInc,ColumnInc;
bool Mark[MAXN][MAXN];//标记有没有访问
public:
int GetRow();
int GetColumn();
void SetRow(int);
void SetColumn(int);
bool BFS();
void DisplayGrid();
void InitGrid();
void DDALine(int,int,int,int);
}Grid;
/************************************************
*函数名GetRow
*无参数
*获得方格行数
*************************************************/
int grid::GetRow()
{
return this->Row;
}
/************************************************
*函数名GetColumn
*无参数
*获得方格列数
*************************************************/
int grid::GetColumn()
{
return this->Column;
}
/************************************************
*函数名SetRow
*无参数
*设置方格行数
*************************************************/
void grid::SetRow(int row)
{
this->Row=row;
}
/************************************************
*函数名SetColumn
*无参数
*设置方格列数
*************************************************/
void grid::SetColumn(int column)
{
this->Column=column;
}
/************************************************
*函数名BFS
*无参数
*利用广度优先寻找最短路径
*************************************************/
bool grid::BFS()
{
state Now,Next;
while(!Qu.empty())
Qu.pop();
Start.path.clear();
Qu.push(Start);
while(!Qu.empty())
{
Now=Qu.front();Qu.pop();
if(Now.x==Target.x&&Now.y==Target.y)
{
this->OptimalPath=Now.path;
cout<<OptimalPath<<endl;
return true;
}
for(int i=0;i<4;i++)
{
int tx=Now.x+Move[i][0];
int ty=Now.y+Move[i][1];
if(!(tx<0||tx>=this->Row||ty<0||ty>=this->Column||Mark[tx][ty]))
{
Next.x=tx;
Next.y=ty;
Next.path=Now.path;
/*
if(0==i)Next.path+='U';
else if(1==i)Next.path+='D';
else if(2==i)Next.path+='L';
else if(3==i)Next.path+='R';
this->Mark[tx][ty]=true;
*/
if(0==i)Next.path+="10";
else if(1==i)Next.path+="00";
else if(2==i)Next.path+="11";
else if(3==i)Next.path+="01";
this->Mark[tx][ty]=true;
Qu.push(Next);
}
}
}
return false;
}
/*******************************************************
*函数名DDALine
*无参数
*利用数值微分法由确定的两个端点画直线
********************************************************/
void grid::DDALine(int lx1,int ly1,int lx2,int ly2)
{
int dx,dy,epsl,k;
float x,y,xIncre,yIncre;
dx=lx2-lx1; dy=ly2-ly1;
x=lx1; y=ly1;
if(abs(dx)>abs(dy))
epsl=abs(dx);
else epsl=abs(dy);
xIncre=(float)dx/(float)epsl;
yIncre=(float)dy/(float)epsl;
glBegin(GL_POINTS);//
for(k=0;k<=epsl;k++)
{
glVertex2i(int(x+0.5),int(y+0.5));
x+=xIncre;
y+=yIncre;
}
glEnd();
}
/*******************************************************
*函数名InitGrid
*无参数
*显示每局的障碍、起点、目标点
********************************************************/
void grid::InitGrid()
{
this->UsedPointNumber=0;
this->TotalPointNumber=this->Row*this->Column;
this->RowInc=winHeight/this->Row,this->ColumnInc=winWidth/this->Column;
memset(this->Mark,false,sizeof(this->Mark));
srand((unsigned)clock());
do
{
this->UsedPointNumber=rand()%(this->TotalPointNumber);
}while(this->UsedPointNumber>=this->TotalPointNumber/4||this->UsedPointNumber<=this->TotalPointNumber/8);
//尽可能合理的控制障碍的数目
int tmp=0;
while(tmp<this->UsedPointNumber)//产生障碍的坐标并尽可能保证适当数目的障碍连成一串
{
int x=rand()%(this->Row),y=rand()%(this->Column),bel=rand()%2;
if(0==bel)//(x-1,y),(x,y),(x+1,y)
{
if(x-1>=0)
{
this->Point[tmp].y=y;this->Point[tmp].x=x-1;tmp++;
this->Mark[x-1][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(x<this->Row)
{
this->Point[tmp].y=y;this->Point[tmp].x=x;tmp++;
this->Mark[x][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(x+1<this->Row)
{
this->Point[tmp].y=y;this->Point[tmp].x=x+1;tmp++;
this->Mark[x+1][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
}
else //(x,y-1),(x,y),(x,y+1)
{
if(y-1>=0)
{
this->Point[tmp].y=y-1;this->Point[tmp].x=x;tmp++;
this->Mark[x][y-1]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(y<this->Column)
{
this->Point[tmp].y=y;this->Point[tmp].x=x;tmp++;
this->Mark[x][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(y+1<this->Column)
{
this->Point[tmp].y=y+1;this->Point[tmp].x=x;tmp++;
this->Mark[x][y+1]=true;
if(tmp>=this->UsedPointNumber)break;
}
}
}
int sx,sy,tx,ty;
do
{
do
{
sx=rand()%(this->Row);
sy=rand()%(this->Column);
}while(this->Mark[sx][sy]);//控制起点无障碍物
do
{
tx=rand()%(this->Row);
ty=rand()%(this->Column);
}while(this->Mark[tx][ty]);//控制目标点无障碍物
}while(abs(sx-tx)+abs(sy-ty)<(this->Row+this->Column)/3);//控制起点和目标点保持适当远的距离不小于方格任意两点最大哈夫曼距离的三分之一
this->Mark[sx][sy]=true;
Start.x=sx;Start.y=sy;
// Mark[tx][ty]=true;
Target.x=tx;Target.y=ty;
DisplayGrid();
if(IsRun)First=false;
}
/*******************************************************
*函数名DisplayGrid
*无参数
*显示窗口的当前状态
********************************************************/
void grid::DisplayGrid()
{
int Left,Right,button,top;
Left=0,Right=winWidth,button=0,top=winHeight;
int lx1,ly1,lx2,ly2;
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f,0.0f,1.0f);
glPointSize(5);
//绘制放个水平线
for(int i=0;i<=winWidth;i+=this->ColumnInc)
{
DDALine(Left+i,button,Left+i,top);
}
//绘制放个竖直线线
for(int i=0;i<=winHeight;i+=this->RowInc)
{
DDALine(Left,button+i,Right,button+i);
}
//绘制障碍物
for(int i=0;i<this->UsedPointNumber;i++)
{
glColor3f(1.0f,0.0f,0.0f);
//glRectf(Left+PerRow[i]*ColumnInc,button+PerColumn[i]*RowInc,Left+PerRow[i]*ColumnInc+ColumnInc,button+PerColumn[i]*RowInc+RowInc);
glRectf(Left+this->Point[i].y*this->ColumnInc,button+this->Point[i].x*this->RowInc,
Left+this->Point[i].y*this->ColumnInc+this->ColumnInc,button+this->Point[i].x*this->RowInc+this->RowInc);
}
int inc=3;
glColor3f(1.0f,1.0f,0.0f);
glRectf(Left+Start.y*this->ColumnInc+inc,button+Start.x*this->RowInc+inc,
Left+Start.y*this->ColumnInc+this->ColumnInc-inc,button+Start.x*this->RowInc+this->RowInc-inc);
glColor3f(1.0f,.0f,1.0f);
glRectf(Left+Target.y*this->ColumnInc+inc,button+Target.x*this->RowInc+inc,
Left+Target.y*this->ColumnInc+this->ColumnInc-inc,button+Target.x*this->RowInc+this->RowInc-inc);
if(!First)//不是第一次初始化窗口,则会出现相应染色体对应的路径
{
int tcnt=this->UsedPointNumber;
BFS();
int size=this->OptimalPath.size();
int tx=Start.x,ty=Start.y;
for(int i=0;i<size-1;i++)
{
if(this->OptimalPath[i]=='D')
{
tx=tx+1;ty=ty;
}
else if(this->OptimalPath[i]=='U')
{
tx=tx-1;ty=ty;
}
else if(this->OptimalPath[i]=='L')
{
tx=tx;ty=ty-1;
}
else if(this->OptimalPath[i]=='R')
{
tx=tx;ty=ty+1;
}
this->Point[this->UsedPointNumber].x=tx;this->Point[this->UsedPointNumber].y=ty;
this->UsedPointNumber++;
}
for(int j=tcnt;j<this->UsedPointNumber;j++)
{
glColor3f(0.0f,1.0f,0.0f);
glRectf(Left+this->Point[j].y*this->ColumnInc,button+this->Point[j].x*this->RowInc,
Left+this->Point[j].y*this->ColumnInc+this->ColumnInc,button+this->Point[j].x*this->RowInc+this->RowInc);
}
this->UsedPointNumber=tcnt;
}
glFlush();
}
/*******************************************************
*函数名init
*无参数
*初始化函数
********************************************************/
void init()
{
glClearColor(0.0f,0.0f,0.0f,1.0f);
glMatrixMode(GL_PROJECTION); //设置投影参数
gluOrtho2D(0.0f, 1000.0f,0.0f,600.0f);
MyLoop=false;
SetRow=false;SetColumn=false;
IsRun=false;
First=true;
}
/*******************************************************
*函数名Display()
*无参数
*窗口创建时显示背景色
********************************************************/
void Display()
{
glClear(GL_COLOR_BUFFER_BIT);
glFlush();
}
/*******************************************************
*函数名ChangeSize
*无参数
*窗口发生变化时完成初始化
********************************************************/
void ChangeSize(int w, int h)
{
winWidth=w;winHeight=h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0,winWidth,0.0,winHeight);
}
/*******************************************************
*函数名timer
*无关参数
*定期刷新窗口
********************************************************/
void Timer(int p)
{
Grid.DisplayGrid();
}
/*******************************************************
*函数名MousePlot
*4个参数:按键类型、动作、对应的坐标
*鼠标响应函数
********************************************************/
void MousePlot(int button,int action,int x,int y)
{
if(SetRow&&SetColumn)
{
if(button==GLUT_LEFT_BUTTON&&action==GLUT_DOWN)
{
if(!MyLoop&&!IsRun)
Grid.InitGrid();
else MyLoop=false;
}
else if(button==GLUT_MIDDLE_BUTTON&&action==GLUT_DOWN)
{
MyLoop=true;
IsRun=true;
First=false;
glutTimerFunc(200,Timer,0);
}
}
}
/*******************************************************
*函数名ProcessMenu
*一个参数,菜单选项
*菜单响应函数
********************************************************/
void ProcessMenu(int value)
{
if(IsRun)//在运行过程中重置方格
{
SetRow=false;
SetColumn=false;
IsRun=false;
First=true;
MyLoop=false;
}
if(value<=10)
{
Grid.SetRow(GridLen[0][value-1]);
SetRow=true;
}
else if(value<=20)
{
Grid.SetColumn(GridLen[1][value-11]);
SetColumn=true;
}
}
/*******************************************************
*函数名MyCreateMenu
*无菜单
*初始化菜单
********************************************************/
void MyCreateMenu()
{
int SetWidth=glutCreateMenu(ProcessMenu);
glutAddMenuEntry("4",1);
glutAddMenuEntry("6",2);
glutAddMenuEntry("8",3);
glutAddMenuEntry("10",4);
glutAddMenuEntry("12",5);
glutAddMenuEntry("14",6);
glutAddMenuEntry("16",7);
glutAddMenuEntry("18",8);
glutAddMenuEntry("20",9);
glutAddMenuEntry("22",10);
int SetHeight=glutCreateMenu(ProcessMenu);
glutAddMenuEntry("4",11);
glutAddMenuEntry("6",12);
glutAddMenuEntry("8",13);
glutAddMenuEntry("10",14);
glutAddMenuEntry("12",15);
glutAddMenuEntry("14",16);
glutAddMenuEntry("16",17);
glutAddMenuEntry("18",18);
glutAddMenuEntry("20",19);
glutAddMenuEntry("22",20);
int Choice=glutCreateMenu(ProcessMenu);
glutAddSubMenu("水平方向方格数",SetWidth);
glutAddSubMenu("垂直方向方格数",SetHeight);
glutCreateMenu(ProcessMenu);
glutAddSubMenu("设置",Choice);
glutAttachMenu(GLUT_RIGHT_BUTTON);
}
int main(int argc, char *argv[])
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_RGB|GLUT_SINGLE);
glutInitWindowPosition(0, 0);
glutInitWindowSize(1000, 600);
glutCreateWindow("BFS算法在方格中的求最短路径动画演示");
glutDisplayFunc(Display);
glutReshapeFunc(ChangeSize);
glutMouseFunc(MousePlot);
MyCreateMenu();
init();
glutMainLoop();
return 0;
}
用BFS引导的
#include<windows.h>
#include<gl/glut.h>
#include<iostream>
#include<string>
#include<vector>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<ctime>
#include<iomanip>
#include<map>
#include<algorithm>
#include<queue>
using namespace std;
const int MAXNGRID=1000;//设置方格的总数
const int MAXROC=50;//设置最大长、宽
const int MAXCHRO=250;//染色体条数
const double eps=1e-10;
int winHeight,winWidth;//当前窗口的长宽
bool MyLoop,SetRow,SetColumn,IsRun,First;//几个开关变量控制鼠标响应
int GridLen[2][10]=
{
{4,6,8,10,12,14,16,18,20,22},
{4,6,8,10,12,14,16,18,20,22}
};
int Move[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
struct state
{
int x,y;
int dis;
string path;
}Start,Target;
queue<state>Qu;
struct point
{
int x,y;
};//建立方格的坐标(规则同OpenGL),便于投影到视区
map<int,string>Mat;
void InitMap()
{
Mat[0]="00";Mat[1]="01";Mat[2]="10";Mat[3]="11";
}
class grid
{
private :
int Row,Column; //方格的行列
int TotalPointNumber,UsedPointNumber; //总的点数、已用点数
int GenerationNum,PopulationSize,MaxDis,MinDis;//繁殖代数、种群规模、最大距离、最短距离
int BetDis[MAXROC][MAXROC];//BetDis[x][y]表示(x,y)到目标点的最短距离
int tcnt; //全局临时变量
string OptimalPath;//遗传算法求得的最短路径
string BFSPath; //BFS算法最短路径
double OptimalFitness;//已找到的最短路径
point Point[MAXNGRID]; //待打印的点
double RowInc,ColumnInc; //窗口的行列步长
bool Mark[MAXROC][MAXROC];//标记有没有访问
double MutationRate; //变异率
double CrossoverRate; //杂交率
double MutationNum; //当代变异个数
double CrossoverNum; //当代交叉个数
int now_Gen; //当前代数
double Fitness[MAXCHRO]; //适应度
double Random[MAXCHRO]; //产生的随机数
double ProSec[MAXCHRO]; //选择概率
double ProAccu[MAXCHRO]; //累积选择概率
vector<string>Chro; //染色体
bool IsUsed[MAXCHRO];//标记当前繁殖代数下该染色体是否已经交叉或变异过
public:
int GetRow();
int GetColumn();
void SetRow(int);
void SetColumn(int);
bool BFS1();
bool BFS2();
void DisplayGrid();
void InitGrid();
void DDALine(int,int,int,int);
void GetMinMaxDis();
bool IsBump(int,int);
bool GetNext(int &,int &,int);
int RunRoute(int &,int &,string &);
double GetFitness(string &);
void Manu_Init();
int GetRand(int);
void Mutation();
void My_Rand();
void Get_Sec_num();
void Selection();
void GetCros(int,int,int,int);
void Crossover();
friend void Timer(int);
friend void MousePlot(int,int,int,int);
}Grid;
/************************************************
*函数名GetRow
*无参数
*获得方格行数
*************************************************/
int grid::GetRow()
{
return this->Row;
}
/************************************************
*函数名GetColumn
*无参数
*获得方格列数
*************************************************/
int grid::GetColumn()
{
return this->Column;
}
/************************************************
*函数名SetRow
*无参数
*设置方格行数
*************************************************/
void grid::SetRow(int row)
{
this->Row=row;
}
/************************************************
*函数名SetColumn
*无参数
*设置方格列数
*************************************************/
void grid::SetColumn(int column)
{
this->Column=column;
}
/******************************************************************************
*函数名GetMinMaxDis
*无参数
*计算路径可能的最小距离和最大距离
*******************************************************************************/
void grid::GetMinMaxDis()
{
this->MaxDis=(this->Row)*(this->Column);
this->MinDis=abs(Target.x-Start.x)+abs(Target.y-Start.y);
}
/******************************************************************************
*函数名IsBump
*两个参数分别表示横坐标、纵坐标
*判断当前是否合法,及是否撞墙或越界
*******************************************************************************/
bool grid::IsBump(int tRow,int tColumn)
{
if(tRow<0||tRow>=this->Row||tColumn<0||tColumn>=this->Column||this->Mark[tRow][tColumn])
return true;
return false;
}
/******************************************************************************
*函数名GetNext
*当前的坐标,移动方向
*若下一个是合法状态,移到该状态,返回true;否则不做操作返回false
*******************************************************************************/
bool grid::GetNext(int &tRow,int &tColumn,int tDirection)
{
int incx,incy;
if(0==tDirection) incx=1,incy= 0;
else if(1==tDirection) incx= 0,incy= 1;
else if(2==tDirection) incx= -1,incy= 0;
else incx= 0,incy=-1;
if(!(this->IsBump(tRow+incx,tColumn+incy)))
{
tRow=tRow+incx,tColumn=tColumn+incy;
return true;//当前方向有效
}
return false;//当前方向无效
}
/******************************************************************************
*函数名:RunRoute
*3个参数分别表示当前点的坐标,和当前处理染色体的引用
* 寻找并记录染色体对应的有效路径同时修改不合法的染色体
*******************************************************************************/
int grid::RunRoute(int &tRow,int &tColumn,string &Chromosome)
{
int size=Chromosome.size();
int Direction;
int len=1;
string newchro;
string tmp;
for(int i=0;i<size;i+=2)
{
tmp.clear();
tmp+=Chromosome[i];
tmp+=Chromosome[i+1];
if(tmp=="00")
{
Direction=0;
}
else if(tmp=="01")
{
Direction=1;
}
else if(tmp=="10")
{
Direction=2;
}
else
{
Direction=3;
}
int tR=tRow,tC=tColumn;
while(!this->GetNext(tRow,tColumn,Direction))
//当前方向不合法,则转到下一方向;如果除去来的其他3个方向都不合法,则返回当前位置的前一个位置
//此处最好的方法是回溯法,类比深搜,但时间复杂度是不能接受的,最坏可达O(4^n)
{
Direction=(Direction+1)%4;
tmp=Mat[Direction];
}
Chromosome[i]=tmp[0];//修正染色体
Chromosome[i+1]=tmp[1];
newchro+=tmp;
if(tRow==Target.x&&tColumn==Target.y)
{
Chromosome=newchro;//找到目标点也做修改染色体,保证路径尽可能短
return len;
}
this->Point[this->UsedPointNumber].x=tRow;
this->Point[this->UsedPointNumber].y=tColumn;
this->UsedPointNumber++;
len++;
}
return len;
}
/******************************************************************************
*函数名GetFitness
*一个参数为当前处理染色体的引用
*计算个体适应度
*******************************************************************************/
double grid::GetFitness(string &Chromosome)
{
int Row=Start.x,Column=Start.y;
int len=this->RunRoute(Row,Column,Chromosome);
if(Row==Target.x&&Column==Target.y)
{
return 1.0;
}
//double tmpdis=abs(Target.x-Row)+abs(Target.y-Column);
double tmpdis=this->BetDis[Row][Column];//此时tmpdis表示到目标点的最短路径长
double ret=1-tmpdis/(this->MaxDis);
//double ret=1.0*(1-tmpdis/MaxDis)+1.0/len;//保证len不为0
return ret;
}
/******************************************************************************
*函数名ChromosomeCmp
*两个参数,分别表示两条染色体
*依据长度从小到大对染色体进行排序,方便交叉
*******************************************************************************/
bool ChromosomeCmp(string tmpa,string tmpb)
{
return tmpa.size()<tmpb.size();
}
/******************************************************************************
*函数名Manu_Init
*无参数
*随机初始化种群
难点在于染色体长度和表征的路径的控制,在此我没有找到对应随机游戏局面的比较好的初始化方案
原因在于局面是随机任意的,且找路径的个体是看不知全局的,只能随便跑,我认为人为干预是不恰当的
*******************************************************************************/
void grid::Manu_Init()
{
this->Chro.clear();
this->GetMinMaxDis(); //获得最大值、最小值
int minlen=this->MinDis;
int maxlen=((this->MaxDis)-(this->UsedPointNumber))/3;
this->PopulationSize=200;///
this->GenerationNum=1000;
srand((unsigned)clock());
string tmp;
for(int i=0;i<this->PopulationSize;i++)
{
tmp.clear();
int len;
do
{
len=rand()%maxlen;
if(len%2)len++;//保证染色体长度为偶数
}while(len<minlen);//控制染色体长度在[minlen,maxlen)之间
while(len)
{
int id=rand()%4;
tmp+=Mat[id];
len--;
}
(this->Chro).push_back(tmp);
}
this->OptimalPath=this->Chro[0];
this->OptimalFitness=0;
this->CrossoverRate=0.5;
this->MutationRate=0.05;
}
/******************************************************************************
*函数名GetRand
*一个参数,表示上限
*返回【0,len)的随机数
*******************************************************************************/
int grid::GetRand(int len)
{
double be=1.0/(len);
double Rand=1.0*rand()/(RAND_MAX);
int ret=(int)(Rand/be);
if(ret>=len)ret--;
return ret;
}
/******************************************************************************
*函数名Mutation()
* 无参数
*随机选染色体,再随机选一个基因片段变异,变异方向不确定
*******************************************************************************/
void grid::Mutation()
{
int belong,id,to,size=this->Chro.size();
string tmp;
srand((unsigned)clock());
memset(this->IsUsed,0,sizeof(this->IsUsed));
while(this->MutationNum>1)
{
do
{
do
{
belong=this->GetRand(size);//属于哪个染色体
}while(this->IsUsed[belong]);//选择当前代没变异过的
id=this->GetRand(this->Chro[belong].size()/2);//变异那个片段
to=GetRand(4);
tmp.clear();
tmp=this->Chro[belong];
tmp[id*2]=Mat[to][0];
tmp[id*2+1]=Mat[to][1];
}while(tmp==this->Chro[belong]);//保证变异后与原来不同
this->Chro[belong]=tmp;
this->MutationNum-=1;
}
}
/******************************************************************************
*函数名My_Rand
*无参数
*产生一组[0,1]内的分布均匀的随机数
*******************************************************************************/
void grid::My_Rand()
{
srand((unsigned)clock());
int size=this->Chro.size();
for(int i=0;i<size;i++)
{
this->Random[i]=1.0*rand()/RAND_MAX;
}
}
/******************************************************************************
*函数名Get_Sec_num
*无参数
*利用赌轮选择法选择适应度大的生存下来
*******************************************************************************/
void grid::Get_Sec_num()
{
this->My_Rand();
vector<string>TmpChromosome;
int j=0;
int size=this->Chro.size();
while(j<size)
{
int i;
for(i=1;i<=size;i++)
{
if(this->Random[j]<=this->ProAccu[i]+eps)//防止浮点数误差
{
TmpChromosome.push_back(this->Chro[i-1]);
j++;
break;
}
}
}
for(int i=0;i<size;i++)
this->Chro[i]=TmpChromosome[i];
TmpChromosome.clear();
}
/******************************************************************************
*函数名
*无参数
*遗传操作-选择主函数
*******************************************************************************/
void grid::Selection()
{
int size=this->Chro.size();
double sum=0;
this->OptimalFitness=0;
this->OptimalPath.clear();
for(int i=0;i<size;i++)
{
sum+=this->Fitness[i];
if(this->Fitness[i]>this->OptimalFitness||((fabs(this->Fitness[i]-this->OptimalFitness)<=eps)&&this->OptimalPath.size()>this->Chro[i].size()))
{
this->OptimalFitness=this->Fitness[i];
this->OptimalPath=this->Chro[i];
}
}
for(int i=1;i<=size;i++)
{
this->ProSec[i]=this->Fitness[i-1]/sum;
}
this->ProAccu[0]=0;
for(int i=1;i<=size;i++)
this->ProAccu[i]=this->ProAccu[i-1]+this->ProSec[i];
this->Get_Sec_num();
}
/******************************************************************************
*函数名GetCros
*4个参数,分别表示带交叉的两条染色体的下标,以及对应的交叉位置
*功能遗传操作-交叉函数
*******************************************************************************/
void grid::GetCros(int One,int Two,int From,int To)
{
string tmp;
for(int i=From;i<=To;i++)
{
tmp.clear();
tmp+=this->Chro[One][i*2];
tmp+=this->Chro[One][i*2+1];
this->Chro[One][i*2]=this->Chro[Two][i*2];
this->Chro[One][i*2+1]=this->Chro[Two][i*2+1];
this->Chro[Two][i*2]=tmp[0];
this->Chro[Two][i*2+1]=tmp[1];
}
}
/******************************************************************************
*函数名Crossover
*无参数
*功能遗传操作-交叉主函数,选择相同长度的染色体进行交叉
*******************************************************************************/
void grid::Crossover()
{
sort(this->Chro.begin(),this->Chro.end(),ChromosomeCmp);
int id,id1,id2,size=this->Chro.size();
bool flag;
memset(this->IsUsed,0,sizeof(this->IsUsed));
while(this->CrossoverNum>1.0)
{
flag=false;
do
{
id=this->GetRand(size);
}while(this->IsUsed[id]);//选择没交叉过的染色体
int tsize=(this->Chro[id]).size();
///选择长度相同且没交叉过的染色体
if(id!=0&&!(this->IsUsed[id-1])&&tsize==this->Chro[id-1].size())
{
flag=true;
do
{
id1=this->GetRand(tsize/2);
id2=this->GetRand(tsize/2);
}while(id1>id2);
this->GetCros(id,id-1,id1,id2);
}
if(!flag&&id!=size-1&&!(this->IsUsed[id+1])&&tsize==this->Chro[id+1].size())
{
flag=true;
do
{
id1=this->GetRand(tsize/2);
id2=this->GetRand(tsize/2);
}while(id1>id2);
this->GetCros(id,id+1,id1,id2);
}
if(flag)this->CrossoverNum-=1;
}
}
/************************************************
*函数名BFS
*无参数
*利用广度优先预处理所有的点到目标点的最近距离
*************************************************/
bool grid::BFS1()
{
state Now,Next;
while(!Qu.empty())
Qu.pop();
Qu.push(Target);
Target.dis=0;
bool Visited[MAXROC][MAXROC];
memcpy(Visited,Mark,sizeof(Mark));
Visited[Target.x][Target.y]=true;
while(!Qu.empty())
{
Now=Qu.front();Qu.pop();
for(int i=0;i<4;i++)
{
int tx=Now.x+Move[i][0];
int ty=Now.y+Move[i][1];
int dis=Now.dis+1;
if(!(tx<0||tx>=this->Row||ty<0||ty>=this->Column||Visited[tx][ty]))
{
Next.x=tx;
Next.y=ty;
Next.dis=dis;
this->BetDis[tx][ty]=dis;
Visited[tx][ty]=true;
Qu.push(Next);
}
}
}
return false;
}
/************************************************
*函数名BFS
*无参数
*利用广度优先寻找最短路径
*************************************************/
bool grid::BFS2()
{
state Now,Next;
while(!Qu.empty())
Qu.pop();
Start.path.clear();
bool Visited[MAXROC][MAXROC];
memcpy(Visited,Mark,sizeof(Mark));
Visited[Target.x][Target.y]=false;
Visited[Start.x][Start.y]=true;
Qu.push(Start);
while(!Qu.empty())
{
Now=Qu.front();Qu.pop();
if(Now.x==Target.x&&Now.y==Target.y)
{
this->OptimalPath=Now.path;
this->OptimalFitness=1.0;
return true;
}
for(int i=0;i<4;i++)
{
int tx=Now.x+Move[i][0];
int ty=Now.y+Move[i][1];
if(!(tx<0||tx>=this->Row||ty<0||ty>=this->Column||Visited[tx][ty]))
{
Next.x=tx;
Next.y=ty;
Next.path=Now.path;
if(0==i)Next.path+="10";
else if(1==i)Next.path+="00";
else if(2==i)Next.path+="11";
else if(3==i)Next.path+="01";
Visited[tx][ty]=true;
Qu.push(Next);
}
}
}
return false;
}
/*******************************************************
*函数名DDALine
*无参数
*利用数值微分法由确定的两个端点画直线
********************************************************/
void grid::DDALine(int lx1,int ly1,int lx2,int ly2)
{
int dx,dy,epsl,k;
float x,y,xIncre,yIncre;
dx=lx2-lx1; dy=ly2-ly1;
x=lx1; y=ly1;
if(abs(dx)>abs(dy))
epsl=abs(dx);
else epsl=abs(dy);
xIncre=(float)dx/(float)epsl;
yIncre=(float)dy/(float)epsl;
glBegin(GL_POINTS);//
for(k=0;k<=epsl;k++)
{
glVertex2i(int(x+0.5),int(y+0.5));
x+=xIncre;
y+=yIncre;
}
glEnd();
}
/*******************************************************
*函数名InitGrid
*无参数
*显示每局的障碍、起点、目标点
********************************************************/
void grid::InitGrid()
{
this->UsedPointNumber=0;
this->TotalPointNumber=this->Row*this->Column;
this->RowInc=winHeight/this->Row,this->ColumnInc=winWidth/this->Column;
memset(this->Mark,false,sizeof(this->Mark));
srand((unsigned)clock());
do
{
this->UsedPointNumber=rand()%(this->TotalPointNumber);
}while(this->UsedPointNumber>=this->TotalPointNumber/4||this->UsedPointNumber<=this->TotalPointNumber/8);
//尽可能合理的控制障碍的数目
int tmp=0;
while(tmp<this->UsedPointNumber)//产生障碍的坐标并尽可能保证适当数目的障碍连成一串
{
int x=rand()%(this->Row),y=rand()%(this->Column),bel=rand()%2;
if(0==bel)//(x-1,y),(x,y),(x+1,y)
{
if(x-1>=0)
{
this->Point[tmp].y=y;this->Point[tmp].x=x-1;tmp++;
this->Mark[x-1][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(x<this->Row)
{
this->Point[tmp].y=y;this->Point[tmp].x=x;tmp++;
this->Mark[x][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(x+1<this->Row)
{
this->Point[tmp].y=y;this->Point[tmp].x=x+1;tmp++;
this->Mark[x+1][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
}
else //(x,y-1),(x,y),(x,y+1)
{
if(y-1>=0)
{
this->Point[tmp].y=y-1;this->Point[tmp].x=x;tmp++;
this->Mark[x][y-1]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(y<this->Column)
{
this->Point[tmp].y=y;this->Point[tmp].x=x;tmp++;
this->Mark[x][y]=true;
if(tmp>=this->UsedPointNumber)break;
}
if(y+1<this->Column)
{
this->Point[tmp].y=y+1;this->Point[tmp].x=x;tmp++;
this->Mark[x][y+1]=true;
if(tmp>=this->UsedPointNumber)break;
}
}
}
int sx,sy,tx,ty;
do
{
do
{
sx=rand()%(this->Row);
sy=rand()%(this->Column);
}while(this->Mark[sx][sy]);//控制起点无障碍物
do
{
tx=rand()%(this->Row);
ty=rand()%(this->Column);
}while(this->Mark[tx][ty]);//控制目标点无障碍物
}while(abs(sx-tx)+abs(sy-ty)<(this->Row+this->Column)/3);//控制起点和目标点保持适当远的距离不小于方格任意两点最大哈夫曼距离的三分之一
this->Mark[sx][sy]=true;
Start.x=sx;Start.y=sy;
//this->Mark[tx][ty]=true;
Target.x=tx;Target.y=ty;
this->Manu_Init();
this->DisplayGrid();
this->BFS1();
this->BFS2();
if(IsRun)First=false;
if(IsRun)First=false;
}
/*******************************************************
*函数名DisplayGrid
*无参数
*显示窗口的当前状态
********************************************************/
void grid::DisplayGrid()
{
int Left,Right,button,top;
Left=0,Right=winWidth,button=0,top=winHeight;
int lx1,ly1,lx2,ly2;
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f,0.0f,1.0f);
glPointSize(5);
//绘制放个水平线
for(int i=0;i<=winWidth;i+=this->ColumnInc)
{
DDALine(Left+i,button,Left+i,top);
}
//绘制放个竖直线线
for(int i=0;i<=winHeight;i+=this->RowInc)
{
DDALine(Left,button+i,Right,button+i);
}
//绘制障碍物
for(int i=0;i<this->UsedPointNumber;i++)
{
glColor3f(1.0f,0.0f,0.0f);
glRectf(Left+this->Point[i].y*this->ColumnInc,button+this->Point[i].x*this->RowInc,
Left+this->Point[i].y*this->ColumnInc+this->ColumnInc,button+this->Point[i].x*this->RowInc+this->RowInc);
}
int inc=3;
glColor3f(0.0f,1.0f,0.0f);
glRectf(Left+Start.y*this->ColumnInc+inc,button+Start.x*this->RowInc+inc,
Left+Start.y*this->ColumnInc+this->ColumnInc-inc,button+Start.x*this->RowInc+this->RowInc-inc);
//cout<<"S.x="<<Start.x<<" S.y="<<Start.y<<endl;///
glColor3f(0.0f,.0f,1.0f);
glRectf(Left+Target.y*this->ColumnInc+inc,button+Target.x*this->RowInc+inc,
Left+Target.y*this->ColumnInc+this->ColumnInc-inc,button+Target.x*this->RowInc+this->RowInc-inc);
//cout<<"T.x="<<Target.x<<" T.y="<<Target.y<<endl;///
if(!First)//不是第一次初始化窗口,则会出现相应染色体对应的路径
{
for(int j=this->tcnt;j<this->UsedPointNumber;j++)
{
glColor3f(0.0f,1.0f,0.0f);
glRectf(Left+this->Point[j].y*this->ColumnInc,button+this->Point[j].x*this->RowInc,
Left+this->Point[j].y*this->ColumnInc+this->ColumnInc,button+this->Point[j].x*this->RowInc+this->RowInc);
}
}
glFlush();
}
/*******************************************************
*函数名init
*无参数
*初始化函数
********************************************************/
void init()
{
glClearColor(0.0f,0.0f,0.0f,1.0f);
glMatrixMode(GL_PROJECTION); //设置投影参数
gluOrtho2D(0.0f, 1000.0f,0.0f,600.0f);
MyLoop=false;
SetRow=false;SetColumn=false;
IsRun=false;
First=true;
}
/*******************************************************
*函数名Display()
*无参数
*窗口创建时显示背景色
********************************************************/
void Display()
{
glClear(GL_COLOR_BUFFER_BIT);
glFlush();
}
/*******************************************************
*函数名ChangeSize
*无参数
*窗口发生变化时完成初始化
********************************************************/
void ChangeSize(int w, int h)
{
winWidth=w;winHeight=h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0,winWidth,0.0,winHeight);
}
/*******************************************************
*函数名timer
*无关参数
*定期刷新窗口
********************************************************/
void Timer(int p)
{
Grid.now_Gen++;
if(Grid.now_Gen>=Grid.GenerationNum*Grid.PopulationSize)
{
Grid.OptimalFitness=Grid.GetFitness(Grid.OptimalPath);
Grid.DisplayGrid();
return ;
}
int i=Grid.now_Gen%Grid.PopulationSize;
Grid.tcnt=Grid.UsedPointNumber;
Grid.Fitness[i]=Grid.GetFitness(Grid.Chro[i]);
Grid.DisplayGrid();
Grid.UsedPointNumber=Grid.tcnt;
if(Grid.now_Gen%Grid.PopulationSize==0)
{
cout<<Grid.OptimalPath<<endl;
cout<<"当前已是第"<<Grid.now_Gen/Grid.PopulationSize<<"代种群!"<<endl;
Grid.Selection();
Grid.MutationNum=Grid.PopulationSize*Grid.MutationRate;//计算变异个数
Grid.CrossoverNum=Grid.PopulationSize*Grid.CrossoverRate/2;//计算交叉个数
Grid.Crossover();
Grid.Mutation();
if(Grid.PopulationSize>10)//精英主义(Elitist Strategy)选择///
{
srand((unsigned)clock());
int Index;
for(int i=0;i<10;i++)
{
Index=rand()%Grid.PopulationSize;
Grid.Chro[Index]=Grid.OptimalPath;
}
}
}
if(MyLoop)
glutTimerFunc(200,Timer,0);
}
/*******************************************************
*函数名MousePlot
*4个参数:按键类型、动作、对应的坐标
*鼠标响应函数
********************************************************/
void MousePlot(int button,int action,int x,int y)
{
if(SetRow&&SetColumn)
{
if(button==GLUT_LEFT_BUTTON&&action==GLUT_DOWN)
{
if(!MyLoop&&!IsRun)
{
memset(Grid.BetDis,0,sizeof(Grid.BetDis));
Grid.InitGrid();
}
else MyLoop=false;
}
else if(button==GLUT_MIDDLE_BUTTON&&action==GLUT_DOWN)
{
MyLoop=true;
IsRun=true;
First=false;
Grid.now_Gen=0;
cout<<"当前已是第"<<Grid.now_Gen/Grid.PopulationSize<<"代种群!"<<endl;
Grid.MutationNum=0;//交叉个数为0
Grid.CrossoverNum=0;//变异个数为0以上是关于人工智能-遗传算法解决推箱子问题现实的主要内容,如果未能解决你的问题,请参考以下文章