经典面试算法题:线性查找有序二维数组
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典面试算法题:线性查找有序二维数组相关的知识,希望对你有一定的参考价值。
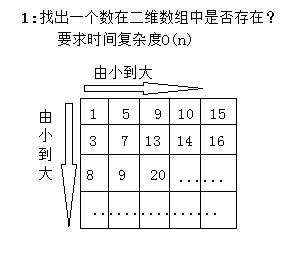
从右上角开始搜索,当前的元素map[x][y]和要搜索的数n有如下可能:
map[x][y]==n --> 返回true
map[x][y]>n --> 向左移动
map[x][y]<n --> 向下移动
搜索过程例子:
AC代码:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int m=sc.nextInt(); int k=sc.nextInt(); int x[][]=new int[n][m]; for(int i=0;i<n;i++){ for(int j=0;j<m;j++){ x[i][j]=sc.nextInt(); } } boolean ans=search(x,k); System.out.println(ans); } public static boolean search(int map[][],int n){ int x=0,y=map.length-1; while(x<map.length && y>=0){ if(map[x][y]==n) return true; else if(map[x][y]<n) x++; else if(map[x][y]>n) y--; } return false; } }
生成测试数据的代码:
import java.util.Random; public class Main_007 { public static void main(String[] args) { int x[][]=gen(10,10); show(x); } public static int[][] gen(int n,int m){ int res[][]=new int[n][m]; for(int i=0;i<n;i++){ for(int j=0;j<m;j++){ int max=0; if(i-1>=0) max=res[i-1][j]; if(j-1>=0) max=Math.max(max,res[i][j-1]); res[i][j]=new Random().nextInt(10)+max+1; } } return res; } public static void show(int x[][]){ for(int i=0;i<x.length;i++){ for(int j=0;j<x[i].length;j++){ System.out.printf("%3d ",x[i][j]); } System.out.println(); } } }
以上是关于经典面试算法题:线性查找有序二维数组的主要内容,如果未能解决你的问题,请参考以下文章