[读书笔记]机器学习：实用案例解析

Posted 2020-08-15 gy_jerry

第7章  优化：密码破译

优化简介：最优点（optimum），优化（optimization）

本章研究的问题：构建一个简单的密码破译系统，把解密一串密文当做一个优化问题。

优化方法：网格搜索（grid search），主要问题是1、步长的选择；2、维度灾难（Curse of Dimensionality）：问题规模过大

optim函数：比网格搜索更快，可以通过已经计算出的信息推断出下一步的方向，同时对所有变量一起优化。(根据书中后文，可能的原理是根据导数得出下一步的进行方向，因为该函数对于不可导点的极值预测性能较差)(书中提到了参考凸优化的原理可以解决optim函数的问题，即绝对值误差优化)

岭回归（ridge regression）：是一种特殊的回归，包含了正则化，与最小二乘法的区别在于其把回归系数本身当做误差项的一部分，这促使回归系数变小。

除了改变误差函数外，岭回归增加的唯一复杂度在于，引入超参数lambda，来权衡我们是希望有较小的平方误差，还是希望有较小的a和b以避免过拟合。（注：正则化算法中引入的该类参数称为超参数，需要根据实际需要或交叉验证选定最优的超参数）

#一个简单的岭回归的例子

ridge.error <- function(heights.weights, a, b, lambda) {
  predictions <- with(heights.weights, height.to.weight(Height, a, b))
  errors <- with(heights.weights, Weight - predictions)
  return(sum(errors ^ 2) + lambda * (a ^ 2 + b ^ 2))
}
lambda <- 1
optim(c(0,0), 
      function(x) {
        ridge.error(heights.weights, x[1], x[2], lambda)
      })

　　

#optim函数用法：1 把打算优化的参数封装在一个数值向量里(c(0,0))
# 　　　　　　　  2 传递的第二个参数是一个匿名函数，这个函数接受一个数值向量(x)作为输入，该数值向量包含了想要优化的目标变量
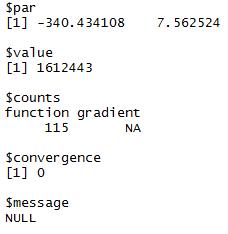
#结果说明：1 par 最优参数对
# 　　　　  2 value 返回最优点时，误差具体值
# 　　　　  3 counts 执行输入函数(function)和梯度(gradient)的次数
# 　　　　  4 convergence 是否足够有把握找到最优点(一切没问题时该值为0，其他值可以在帮助文档中找到对应信息)
# 　　　　  5 message 其他信息

 用优化的思路解决密码破译问题：

随机优化：在可选的输入参数范围内，一定程度上随机的移动参数（保证移动参数的方向是误差减少的方向）。比较典型的有模拟退火算法、遗传算法以及马尔科夫链蒙特卡洛方法（Markov Chain Monte Carlo, MCMC）。本文中采用的算法是Metropolis方法

问题描述：

1、为每一种解密规则定义一个解密效果度量；

2、定义一个基于目前已知的解密效果最优的解密规则的算法，对它进行随机修改来生成一个新的解密规则；

3、定义一个算法，可以递进地生成破译效果逐渐变好的解密规则。

在此之前，完成密码的加密过程：

凯撒密码及其R语言实现：明文中的一个字母用另一个固定字母替代

english.letters <- c(\'a\', \'b\', \'c\', \'d\', \'e\', \'f\', \'g\', \'h\', \'i\', \'j\', \'k\', \'l\', \'m\', \'n\', 
                     \'o\', \'p\', \'q\', \'r\', \'s\', \'t\', \'u\', \'v\', \'w\', \'x\', \'y\', \'z\')
caesar.cipher <- list()
inverse.caesar.cipher <- list()

for (index in 1:length(english.letters)) {
  caesar.cipher[[english.letters[index]]] <- english.letters[index %% 26 + 1]
  inverse.caesar.cipher[[english.letters[index %% 26 + 1]]] <- english.letters[index]
}
print(caesar.cipher)

　　

加密函数：

apply.cipher.to.string <- function(string, cipher) {
  output <- \'\'
  for (i in 1:nchar(string)) {
    output <- paste(output, cipher[[substr(string, i, i)]], sep = \'\')
  }
  return(output)
}
apply.cipher.to.text <- function(text, cipher) {
  output <- c()
  for (string in text) {
    output <- c(output, apply.cipher.to.string(string, cipher))
  }
  return(output)
}
apply.cipher.to.text(c(\'sample\', \'text\'), caesar.cipher)

　　

1、解密效果的评价：解密出的词是有意义的，可以通过计算揭秘出的单词在词典中出现的概率来评价，将词组所有的词的概率相乘，就得到了词组的解密效果的评价指标（按照一般的逻辑，还应该有语法支持，不过这里并不讨论）

具体实现方式：Metropolis方法。首先从一个随机的解密规则开始，然后通过多次循环优化它，直到最后它就有可能成为一个正确的解密规则。

2、通过现有的解密规则得到一个新的解密规则：首先随机改变当前规则的一处，只有当新解密规则得到的解密串概率变高时，才接受新的解密规则（贪心优化），但是这个例子中，有可能一个“坏”的解密规则的解密串概率要大于“好”的，因此使用如下的优化方式：

　　设原解密规则为A，新解密规则为B

　　如果解密规则B解密出的解密串的概率大于解密规则A对应的解密串，那么我们用B代替A

　　如果解密规则B解密出的解密串的概率小于解密规则A对应的解密串，则用B代替A的概率为probability(T, B)/probability(T, A)

 

处理解密规则的工具

#产生随机加密规则
generate.random.cipher <- function() {
  cipher <- list()
  
  inputs <- english.letters
  outputs <- english.letters[sample(1:length(english.letters), length(english.letters))]
  
  for (index in 1:length(english.letters)) {
    cipher[[inputs[index]]] <- outputs[index]
  }
  return(cipher)
}

modify.cipher <- function(cipher, input, output) {
  new.cipher <- cipher
  new.cipher[[input]] <- output
  old.output <- cipher[[input]]
  collateral.input <- names(which(sapply(names(cipher), function(key){cipher[[key]]}) == output))
  new.cipher[[collateral.input]] <- old.output
  return(new.cipher)
}

propose.modefied.cipher <- function(cipher) {
  input <- sample(names(cipher), 1)
  output <- sample(english.letters, 1)
  return(modify.cipher(cipher, input, output))
}

　　

弱化版的贪心算法：计算probability(T, B)/probability(T, A)，再把它与一个0~1的随机数比较，若随机数大，就更换当前规则，否则不变

#加载词典
load(\'ML_for_Hackers/07-Optimization/data/lexical_database.Rdata\')
#计算文本概率的函数
one.gram.probability <- function(one.gram, lexical.database = list()) {
  lexical.probability <- lexical.database[[one.gram]]
  
  #R语言中最小的浮点数是.Machine$double.eps
  if (is.null(lexical.probability) || is.na(lexical.probability)) {
    return(.Machine$double.eps)
  } else {
    return(lexical.probability)
  }
}
#对数变换(为了使结果稳定)
log.probability.of.text <- function(text, cipher, lexical.database = list()) {
  log.probability <- 0.0
  
  for (string in text) {
    decrypted.string <- apply.cipher.to.string(string, cipher)
    log.probability <- log.probability + log(one.gram.probability(decrypted.string, lexical.database))
  }
  
  return(log.probability)
}

#单步Metropolis方法
metropolis.step <- function(text, cipher, lexical.database = list()) {
  proposed.cipher <- propose.modefied.cipher(cipher)
  
  lp1 <- log.probability.of.text(text, cipher, lexical.database)
  lp2 <- log.probability.of.text(text, proposed.cipher, lexical.database)
  
  if(lp2 > lp1) {
    return(proposed.cipher)
  } else {
    a <- exp(lp2 - lp1)
    x <- runif(1)
    if (x < a) {
      return(proposed.cipher)
    } else {
      return(cipher)
    }
  }
}

　　

明文与加密：

decrypted.text <- c(\'here\', \'is\', \'some\', \'sample\', \'text\')
encrypted.text <- apply.cipher.to.text(decrypted.text, caesar.cipher)

　　

 

 

解密并保存结果：

set.seed(1)
cipher <- generate.random.cipher()

results <- data.frame()

number.of.iterations <- 50000

for (iteration in 1:number.of.iterations) {
  log.probability <- log.probability.of.text(encrypted.text, cipher, lexical.database)
  current.decrypted.text <- paste(apply.cipher.to.text(encrypted.text, cipher), collapse = \' \')
  correct.text <- as.numeric(current.decrypted.text == paste(decrypted.text, collapse = \' \'))
  results <- rbind(results, 
                   data.frame(Iterations = iteration, 
                              LogProbability = log.probability, 
                              CurrentDecryptedText = current.decrypted.text, 
                              CorrectText = correct.text))
  cipher <- metropolis.step(encrypted.text, cipher, lexical.database)
}

write.table(results, file = \'chapter07_results.csv\', row.names = FALSE, sep = \'\\t\')

　　

由于这种算法度量的是每一个单词是否是一个真正的英文单词，而不考虑连接起来是否通顺，即是否符合语法。这提示了要注意优化问题的复杂性：优化算法得到的最优结果不一定是想要的结果，解决优化问题时不能完全离开人工监督。

其他问题：

首先，Metropolis方法是一个随机优化算法。我们选择的随机种子是1，如果选择了一个不好的随机种子，可能需要执行亿万次循环才能得到正确的解密规则；

其次，Metropolis方法总是乐于放弃好的解密规则，因为这是一个非贪心算法。正因为如此，如果观察足够的时间，会发现它放弃了“真正”的解密规则。这种问题成为随机扰动。

解决这种随机扰动问题有一些方法：

1、模拟退火方法：随着循环次数增多，越来越不可能接受没有变好的规则（即越来越贪心）；

2、接受这种随机性，但是给出的结果不是一个确定的方案，而是一组方案的概率分布。但这种方法只适用于数值型变量的问题。