哈夫曼树

Posted 2020-06-14

定义：给定n个带有权值的叶节点，将其组成一颗带权路径长度最小的二叉树，则该二叉树为哈夫曼树，亦称最优二叉树

假设叶节点的权值分别为w1, w2, w3 ... wn，到根节点的路径长度分别为l1, l2, l3 ... ln，

那么WPL = w1 * l1 + w2 * l2 + w3 * l3 + ... + wn * ln，哈夫曼树则是WPL最小的树

 

构成哈夫曼树算法：

 

样例：

 

 

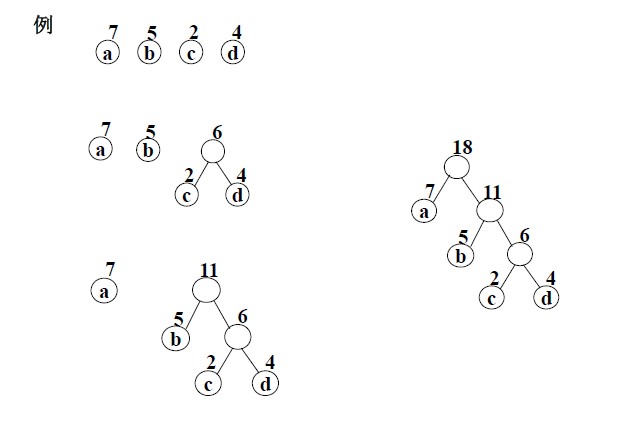
简单示例代码：

 

// Author: Waihui Zheng
// 哈夫曼树

#include <iostream>
#include <string>
#include <vector>
#include <queue>
#include <functional>

namespace my_space {

#define ENDTREE -1

class HaffMan {
    // 哈夫曼树节点
    struct TreeNode {
        int weight;
        int parent;
        int lchild;
        int rchild;

        TreeNode(int w = 0) : weight(w), parent(ENDTREE), lchild(ENDTREE), rchild(ENDTREE) {}
    };

    // 信息节点
    struct NodeInfo {
        std::string info;
        int weight;
        int location;

        NodeInfo(const std::string& str = "", int w = 0)
                : info(str), weight(w), location(ENDTREE) {}
    };

    // 优先队列节点
    struct WeightHelper {
        int weight;
        int index;

        WeightHelper(int w = 0, int ix = -1) : weight(w), index(ix) {}
        bool operator>(const WeightHelper& rhs) const {
            return weight > rhs.weight;
        }
    };

public:
    HaffMan() {}
    ~HaffMan() {}

    void clear() {
        _node_infos.clear();
        _haffman_tree.clear();
    }

    void add_info(const std::string& info, int weight) {
        _node_infos.push_back(NodeInfo(info, weight));
    }

    void construct_haffman_tree() {
        // 初始化哈夫曼树，建立n个独立的树
        _haffman_tree.clear();
        for (int i = 0; i < _node_infos.size(); ++i) {
            _haffman_tree.push_back(TreeNode(_node_infos[i].weight));
            _node_infos[i].location = i;
        }

        // 优先队列，内部按权值进行排序
        std::priority_queue<WeightHelper, std::vector<WeightHelper>, std::greater<WeightHelper> > pq;
        for (int i = 0; i < _haffman_tree.size(); ++i) {
            pq.push(WeightHelper(_haffman_tree[i].weight, i));
        }

        // 生成n-1颗树
        int times = _node_infos.size() - 1;
        while (times--) {
            // 优先找出两颗根权值最小的两颗
            WeightHelper lchild = pq.top();
            pq.pop();
            WeightHelper rchild = pq.top();
            pq.pop();

            // 创建新root节点
            TreeNode new_tree_node(
                    _haffman_tree[lchild.index].weight + _haffman_tree[rchild.index].weight);
            new_tree_node.lchild = lchild.index;
            new_tree_node.rchild = rchild.index;
            _haffman_tree.push_back(new_tree_node);

            // 修改子节点父母节点指针指向
            _haffman_tree[lchild.index].parent = _haffman_tree.size() - 1;
            _haffman_tree[rchild.index].parent = _haffman_tree.size() - 1;

            // 加入新树
            pq.push(WeightHelper(new_tree_node.weight, _haffman_tree.size() - 1));
        }
    }

    std::string get_haffman_code(const std::string& name) {
        int name_index = 0;
        for (; name_index < _node_infos.size(); ++name_index) {
            if (_node_infos[name_index].info == name) {
                break;
            }
        }

        std::string code;
        if (name_index == _node_infos.size()) {
            return code;
        }

        int cur_index = _node_infos[name_index].location;
        int parent_index = _haffman_tree[cur_index].parent;
        // 回溯寻找 叶子节点到根节点的路径
        while (parent_index != ENDTREE) {
            code.push_back(_haffman_tree[parent_index].lchild == cur_index ? ‘0‘ : ‘1‘);

            cur_index = parent_index;
            parent_index = _haffman_tree[cur_index].parent;
        }

        std::reverse(code.begin(), code.end());
        return code;
    }

    void print() {
        for (int i = 0; i < _node_infos.size(); ++i) {
            std::cout << _node_infos[i].info << " code: "
                      << get_haffman_code(_node_infos[i].info) << std::endl;
        }
    }

private:
    std::vector<NodeInfo> _node_infos;
    std::vector<TreeNode> _haffman_tree;
};

}

int main() {
    my_space::HaffMan haffman_tree;
    haffman_tree.add_info("A", 7);
    haffman_tree.add_info("B", 5);
    haffman_tree.add_info("C", 2);
    haffman_tree.add_info("D", 4);

    haffman_tree.construct_haffman_tree();

    haffman_tree.print();
    return 0;
}