搬土距离（Earth Mover's Distance)

Posted 2020-08-15 厚礼的博客

搬土距离（The Earth Mover‘s Distance，EMD）最早由Y. Rubner在1999年的文章《A Metric for Distributions with Applications to Image Databases》中提出，它是归一化的从一个分布变为另一个分布的最小代价，因此可用于表征两个分布之间的距离。

例如，对于图像而言，它可以看做是由色调、饱和度、亮度三个分量组成，每个分量的直方图就是一个分布。不同的图像对应的直方图不同，因此图像之间的距离可以用直方图的距离表征，这时就可以用EMD进行计算。

EMD需要求解运输问题，其运算复杂度较高，平均而言至少是二次方级别。但是它作为距离函数，有一个非常好的特点是存在下界——两个分布的质心之间的距离，因此在粗略计算时，可以考虑用分布质心之间的距离代替EMD。

The Earth Mover‘s Distance

The Earth Mover‘s Distance (EMD) is a method to evaluate dissimilarity between two multi-dimensional distributions in some feature space where a distance measure between single features, which we call the ground distance is given. The EMD ``lifts‘‘ this distance from individual features to full distributions.

Intuitively, given two distributions, one can be seen as a mass of earth properly spread in space, the other as a collection of holes in that same space. Then, the EMD measures the least amount of work needed to fill the holes with earth. Here, a unit of work corresponds to transporting a unit of earth by a unit of ground distance.

A distribution can be represented by a set of clusters where each cluster is represented by its mean (or mode), and by the fraction of the distribution that belongs to that cluster. We call such a representation the signature of the distribution. The two signatures can have different sizes, for example, simple distributions have shorter signatures than complex ones.

Computing the EMD is based on a solution to the well-known transportation problem [1]. Suppose that several suppliers, each with a given amount of goods, are required to supply several consumers, each with a given limited capacity. For each supplier-consumer pair, the cost of transporting a single unit of goods is given. The transportation problem is then to find a least-expensive flow of goods from the suppliers to the consumers that satisfies the consumers‘ demand. Matching signatures can be naturally cast as a transportation problem by defining one signature as the supplier and the other as the consumer, and by setting the cost for a supplier-consumer pair to equal the ground distance between an element in the first signature and an element in the second. Intuitively, the solution is then the minimum amount of ``work‘‘ required to transform one signature into the other.

This can be formalized as the following linear programming problem: Let  be the first signature with m clusters, where p_i is the cluster representative and w_pi is the weight of the cluster;  the second signature with n clusters; and  the ground distance matrix where d_ij is the ground distance between clusters p_i and q_j.

We want to find a flow , with f_ij the flow between p_i and q_j, that minimizes the overall cost 

 

 

 

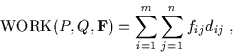
subject to the following constraints: 

 

 

The first constraint allows moving ``supplies‘‘ from P to Q and not vice versa. The next two constraints limits the amount of supplies that can be sent by the clusters in P to their weights, and the clusters in Q to receive no more supplies than their weights; and the last constraint forces to move the maximum amount of supplies possible. We call this amount the total flow. Once the transportation problem is solved, and we have found the optimal flow , the earth mover‘s distance is defined as the work normalized by the total flow: 

 

 

 

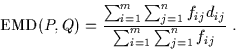
The normalization factor is introduced in order to avoid favoring smaller signatures in the case of partial matching.

The EMD has the following advantages

 

 

• Naturally extends the notion of a distance between single elements to that of a distance between sets, or distributions, of elements.

   

• Can be applied to the more general variable-size signatures, which subsume histograms. Signatures are more compact, and the cost of moving ``earth‘‘ reflects the notion of nearness properly, without the quantization problems of most other measures.

   

• Allows for partial matches in a very natural way. This is important, for instance, for image retrieval and in order to deal with occlusions and clutter.

   

• Is a true metric if the ground distance is metric and if the total weights of two signatures are equal. This allows endowing image spaces with a metric structure.

   

• Is bounded from below by the distance between the centers of mass of the two signatures when the ground distance is induced by a norm. Using this lower bound in retrieval systems significantly reduced the number of EMD computations.

   

• Matches perceptual similarity better than other measures, when the ground distance is perceptually meaningful. This was shown by [2] for color- and texture-based image retrieval.

   

More details on the EMD can be found in [2].

1 F. L. Hitchcock. 

The distribution of a product from several sources to numerous localities.
J. Math. Phys., 20:224-230, 1941.

2 Y. Rubner, C. Tomasi, and L. J. Guibas.
A metric for distributions with applications to image databases.
In IEEE International Conference on Computer Vision, pages 59-66, January 1998.

 

 

From：http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/RUBNER/emd.htm