一系列网络流题目-2016.10.18
Posted PoorLitt1eThin9
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一系列网络流题目-2016.10.18相关的知识,希望对你有一定的参考价值。
稍微修改了一下最大流的算法,昨天整理代码的有错误。本来想把算法封装成一个模板类,结果运行时间直接从2秒变成了超时,那道题总时间是15秒,单点限制5秒。
HDU3416:Marriage Match IV
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3581 Accepted Submission(s): 1056
Problem Description
Do not sincere non-interference。
Like that show, now starvae also take part in a show, but it take place between city A and B. Starvae is in city A and girls are in city B. Every time starvae can get to city B and make a data with a girl he likes. But there are two problems with it, one is starvae must get to B within least time, it\'s said that he must take a shortest path. Other is no road can be taken more than once. While the city starvae passed away can been taken more than once.
So, under a good RP, starvae may have many chances to get to city B. But he don\'t know how many chances at most he can make a data with the girl he likes . Could you help starvae?
Input
The first line is an integer T indicating the case number.(1<=T<=65)
For each case,there are two integer n and m in the first line ( 2<=n<=1000, 0<=m<=100000 ) ,n is the number of the city and m is the number of the roads.
Then follows m line ,each line have three integers a,b,c,(1<=a,b<=n,0<c<=1000)it means there is a road from a to b and it\'s distance is c, while there may have no road from b to a. There may have a road from a to a,but you can ignore it. If there are two roads from a to b, they are different.
At last is a line with two integer A and B(1<=A,B<=N,A!=B), means the number of city A and city B.
There may be some blank line between each case.
Output
Output a line with a integer, means the chances starvae can get at most.
Sample Input
3
7 8
1 2 1
1 3 1
2 4 1
3 4 1
4 5 1
4 6 1
5 7 1
6 7 1
1 7
6 7
1 2 1
2 3 1
1 3 3
3 4 1
3 5 1
4 6 1
5 6 1
1 6
2 2
1 2 1
1 2 2
1 2
Sample Output
2
1
1

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<climits>
#include<queue>
using namespace std;
#define clr(x)memset(x,0,sizeof(x))
#define min(a,b)(a)<(b)?(a):(b)
const int INF=INT_MAX;
const int maxn=1005;
const int maxm=1000000;
struct node
{
int from,to,next,c;
}e[maxm];
int tot;
int head[maxn];
void add(int s,int u,int f1,int f2)
{
e[tot].from=s;
e[tot].to=u;
e[tot].c=f1;
e[tot].next=head[s];
head[s]=tot++;
e[tot].from=u;
e[tot].to=s;
e[tot].c=f2;
e[tot].next=head[u];
head[u]=tot++;
}
int q[maxn];
int cnt[maxn];
int d[maxn];
int low[maxn];
int cur[maxn];
int maxflow(int s,int t,int n)
{
int *front=q,*rear=q;
for(int i=1;i<=n;i++)
{
d[i]=n;
cnt[i]=0;
}
cnt[n]=n-1;
cnt[0]++;
d[t]=0;
*rear++=t;
while(front<rear)
{
int v=*front++;
for(int i=head[v];i!=-1;i=e[i].next)
{
if(d[e[i].to]==n&&e[i^1].c>0)
{
d[e[i].to]=d[v]+1;
cnt[n]--;
cnt[d[e[i].to]]++;
*rear++=e[i].to;
}
}
}
int flow=0, u=s, top=0;
low[0]=INF;
for(int i=1;i<=n;i++)
cur[i]=head[i];
while(d[s]<n)
{
int &i=cur[u];
for(;i!=-1;i=e[i].next)
{
if(e[i].c>0&&d[u]==d[e[i].to]+1)
{
low[top+1]=min(low[top],e[i].c);
q[++top]=i;
u=e[i].to;
break;
}
}
if(i!=-1)
{
if(u==t)
{
int minf=low[top];
for(int p=1,i;p<=top;++p)
{
i=q[p];
e[i].c-=minf;
e[i^1].c+=minf;
}
flow+=minf;
u=s;
low[0]=INF;
top=0;
}
}
else
{
int old_du=d[u];
cnt[old_du]--;
d[u]=n-1;
for(int i=head[u];i!=-1;i=e[i].next)
if(e[i].c>0&&d[u]>d[e[i].to])
d[u]=d[e[i].to];
cnt[++d[u]]++;
if(d[u]<n)
cur[u]=head[u];
if(u!=s)
{
u=e[q[top]].from;
--top;
}
if(cnt[old_du]==0)
break;
}
}
return flow;
}
struct EDGE
{
int from,to,next,w;
}edge[maxm],ee[maxm];
int head2[maxn];
int head3[maxn];
int tt;
int t3;
void add2(int s,int t,int wi)
{
edge[tt].from = s;
edge[tt].to = t;
edge[tt].w = wi;
edge[tt].next = head2[s];
head2[s] = tt++;
}
void add3(int s,int t,int wi)
{
ee[t3].from = s;
ee[t3].to = t;
ee[t3].w = wi;
ee[t3].next = head3[s];
head3[s] = t3++;
}
struct dd
{
int xu, di;
bool operator < (dd t)const{
return t.di<di;
}
}x,in;
priority_queue<dd>dis;
int d1[maxn];
int d2[maxn];
void dijkstra(int u,int*d,int*hed,EDGE*ed,int&t)
{
int i;
in.xu = u;
in.di = 0;
d[u] = 0;
dis.push(in);
while(!dis.empty())
{
x = dis.top();
dis.pop();
for(i = hed[x.xu]; i; i = ed[i].next){
in.xu = ed[i].to;
in.di = x.di+ed[i].w;
if(in.di < d[in.xu]){
d[in.xu] = in.di;
dis.push(in);
}
}
}
}
int main()
{
int T, i;
int n, m, st, en;
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n, &m);
clr(head2);
clr(head3);
tt = 1;
t3 = 1;
int a,b,c;
while(m--)
{
scanf("%d %d %d",&a, &b, &c);
add2(a,b,c);
add3(b,a,c);
}
scanf("%d %d",&st,&en);
for(i = 1; i <= n; i++)
d2[i] = d1[i] = INF;
dijkstra(st,d1,head2,edge,tt);
dijkstra(en,d2,head3,ee,t3);
memset(head,-1,sizeof(head));
tot = 0;
for(i = 1; i < tt; i++)
{
if(d1[edge[i].from]+d2[edge[i].to]+edge[i].w == d1[en])
add(edge[i].from,edge[i].to,1,0);
}
int res = maxflow(st,en,n);
printf("%d\\n",res);
}
return 0;
}
HDU3491:Thieves
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 1604 Accepted Submission(s): 727
Problem Description
In the kingdom of Henryy, there are N (2 <= N <= 100) cities, with M (M <= 10000) two-direct ways connecting them.
A group of thieves from abroad plan to steal the metropolitan museum in city H (It has not been demolished). However, the brave, brilliant, bright police in the kingdom have known this plan long before, and they also plan to catch the thieves. The thieves are in the city S at present. The police try to catch them on their way from S to H. Although the thieves might travel this way by more than one group, our excellent police has already gather the statistics that the number of the people needed in city I (1<=I<=N) to arrest the thieves.
The police do not want to encounter the thieves in either city S or city H.
The police finish the task with the minimum number of people. Do you know the exact number?
Input
The first line contains an integer T (T <= 10), indicating the number of the test cases.
The first line of each test case has four integers: N, the number of the cities; M, the number of the roads; S (1<=S<=N), the label of city S; H (1<=T<=N, S≠H), the label of city H.
The second line contains N integers, indicating the number of people needed in each city. The sum of these N integers is less than 10000.
Then M lines followed, each containing two integers x and y, indicating that there is a two-direct roads between city x and y. Notices that no road between city S and H.
A blank line is followed after each test case.
Output
For each test case, output a single integer in a separate line, indicating the minimum number of people the police used.
Sample Input
1
5 5 1 5
1 6 6 11 1
1 2
1 3
2 4
3 4
4 5
Sample Output
11
这题有点生气,看完题后先去网上搜了一下别人的解法,感觉很多人写的很扯淡,估计从别人那抄的自己都没怎么懂就瞎写一通,有的还说什么从源点到每个点连一条边,从每个点连一条边到汇点,容量都是INF,mdzz。
网络流没问题,拆点没问题,但明显源点和汇点是s和t,而不是什么YY出来的超级源点。
这样建图(箭头指的那个图):
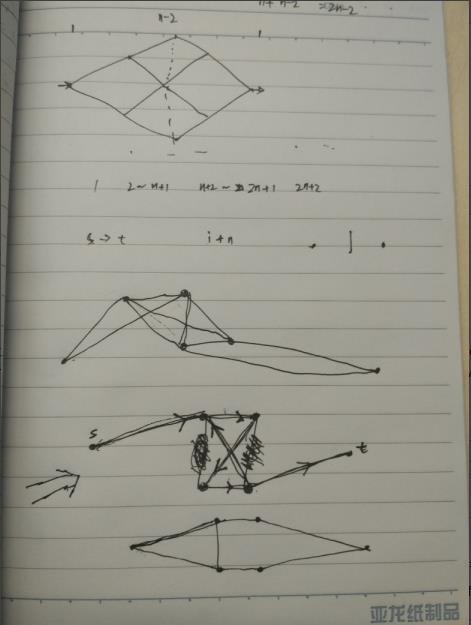
首先,每个点拆成两个点分别是1~n和n+1到2n,分别称为起点和终点。
然后每个点的起点和终点之间连一条弧,从起点指向终点,容量为该点的权值。s点和t点的起点和终点连线的容量为INF。
对于每条边(a,b)连两条弧,分别从a的终点指向b的起点和从b的终点指向a的起点,容量为INF。
计算s到t的最大流,即为最少警力。

#pragma comment(linker, "/STACK:102400000,102400000")
#include <iostream>
#include <algorithm>
#include <string.h>
#include <vector>
#include <map>
#include <queue>
#include <stdlib.h>
using namespace std;
// ALGORITHM_MAXFLOW_SAP ->
#define ALGORITHM_MAXFLOW_SAP_MAXN 20010
#define ALGORITHM_MAXFLOW_SAP_MAXM 880010
#define ALGORITHM_MAXFLOW_SAP_INF 0x7FFFFFFF
struct ALGORITHM_MAXFLOW_SAP_Node {
int from, to, next;
int cap;
} ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_MAXM];
int ALGORITHM_MAXFLOW_SAP_tol;
int ALGORITHM_MAXFLOW_SAP_head[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_dep[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_cur[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_S[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_que[ALGORITHM_MAXFLOW_SAP_MAXN];
int ALGORITHM_MAXFLOW_SAP_n;
void ALGORITHM_MAXFLOW_SAP_clear() {
ALGORITHM_MAXFLOW_SAP_tol = 0;
memset(ALGORITHM_MAXFLOW_SAP_head, -1, sizeof(ALGORITHM_MAXFLOW_SAP_head));
}
void ALGORITHM_MAXFLOW_SAP_addedge(int u, int v, int w) {
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].from = u;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].to = v;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].cap = w;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].next = ALGORITHM_MAXFLOW_SAP_head[u];
ALGORITHM_MAXFLOW_SAP_head[u] = ALGORITHM_MAXFLOW_SAP_tol++;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].from = v;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].to = u;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].cap = 0;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].next = ALGORITHM_MAXFLOW_SAP_head[v];
ALGORITHM_MAXFLOW_SAP_head[v] = ALGORITHM_MAXFLOW_SAP_tol++;
}
void ALGORITHM_MAXFLOW_SAP_BFS(int start, int end) {
memset(ALGORITHM_MAXFLOW_SAP_dep, -1, sizeof(ALGORITHM_MAXFLOW_SAP_dep));
memset(ALGORITHM_MAXFLOW_SAP_gap, 0, sizeof(ALGORITHM_MAXFLOW_SAP_gap));
ALGORITHM_MAXFLOW_SAP_gap[0] = 1;
int front, rear;
front = rear = 0;
ALGORITHM_MAXFLOW_SAP_dep[end] = 0;
ALGORITHM_MAXFLOW_SAP_que[rear++] = end;
while (front != rear) {
int u = ALGORITHM_MAXFLOW_SAP_que[front++];
if (front == ALGORITHM_MAXFLOW_SAP_MAXN) {
front = 0;
}
for (int i = ALGORITHM_MAXFLOW_SAP_head[u]; i != -1; i = ALGORITHM_MAXFLOW_SAP_edge[i].next) {
int v = ALGORITHM_MAXFLOW_SAP_edge[i].to;
if (ALGORITHM_MAXFLOW_SAP_dep[v] != -1) {
continue;
}
ALGORITHM_MAXFLOW_SAP_que[rear++] = v;
if (rear == ALGORITHM_MAXFLOW_SAP_MAXN) {
rear = 0;
}
ALGORITHM_MAXFLOW_SAP_dep[v] = ALGORITHM_MAXFLOW_SAP_dep[u] + 1;
++ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_dep[v]];
}
}
}
int ALGORITHM_MAXFLOW_SAP_SAP(int start, int end) {
int res = 0;
ALGORITHM_MAXFLOW_SAP_BFS(start, end);
int top = 0;
memcpy(ALGORITHM_MAXFLOW_SAP_cur, ALGORITHM_MAXFLOW_SAP_head, sizeof(ALGORITHM_MAXFLOW_SAP_head));
int u = start;
int i;
while (ALGORITHM_MAXFLOW_SAP_dep[start] < ALGORITHM_MAXFLOW_SAP_n) {
if (u == end) {
int temp = ALGORITHM_MAXFLOW_SAP_INF;
int inser;
for (i = 0; i < top; i++)
if (temp > ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap) {
temp = ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap;
inser = i;
}
for (i = 0; i < top; i++) {
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap -= temp;
ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i] ^ 1].cap += temp;
}
res += temp;
top = inser;
u = ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[top]].from;
}
if (u != end && ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_dep[u] - 1] == 0) {
break;
}
for (i = ALGORITHM_MAXFLOW_SAP_cur[u]; i != -1; i = ALGORITHM_MAXFLOW_SAP_edge[i].next)
if (ALGORITHM_MAXFLOW_SAP_edge[i].cap != 0 && ALGORITHM_MAXFLOW_SAP_dep[u] == ALGORITHM_MAXFLOW_SAP_dep[ALGORITHM_MAXFLOW_SAP_edge[i].to] + 1) {
break;
}
if (i != -1) {
ALGORITHM_MAXFLOW_SAP_cur[u] = i;
ALGORITHM_MAXFLOW_SAP_S[top++] = i;
u = ALGORITHM_MAXFLOW_SAP_edge[i].to;
} else {
int min = ALGORITHM_MAXFLOW_SAP_n;
for (i = ALGORITHM_MAXFLOW_SAP_head[u]; i != -1; i = ALGORITHM_MAXFLOW_SAP_edge[i].next) {
if (ALGORITHM_MAXFLOW_SAP_edge[i].cap == 0) {
continue;
}
if (min > ALGORITHM_MAXFLOW_SAP_dep[ALGORITHM_MAXFLOW_SAP_edge[i].to]) {
min = ALGORITHM_MAXFLOW_SAP_dep[ALGORITHM_MAXFLOW_SAP_edge[i].to];
ALGORITHM_MAXFLOW_SAP_cur[u] = i;
}
}
--ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_dep[u]];
ALGORITHM_MAXFLOW_SAP_dep[u] = min + 1;
++ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_dep[u]];
if (u != start) {
u = ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[--top]].from;
}
}
}
return res;
}
// <- ALGORITHM_MAXFLOW_SAP
int main() {
int T, n, m, s, t, a, b, c;
scanf("%d", &T);
while (T--) {
scanf("%d%d%d%d", &n, &m, &s, &t);
ALGORITHM_MAXFLOW_SAP_clear();
for (int i = 1; i <= n; i++) {
scanf("%d", &a);
ALGORITHM_MAXFLOW_SAP_addedge(i, i + n, (i == s || i == t) ? ALGORITHM_MAXFLOW_SAP_INF : a);
}
for (int i = 1; i <= m; i++) {
scanf("%d%d", &a, &b);
ALGORITHM_MAXFLOW_SAP_addedge(a + n, b, ALGORITHM_MAXFLOW_SAP_INF);
ALGORITHM_MAXFLOW_SAP_addedge(b + n, a, ALGORITHM_MAXFLOW_SAP_INF);
}
ALGORITHM_MAXFLOW_SAP_n = 2 * n;
printf("%d\\n", ALGORITHM_MAXFLOW_SAP_SAP(s, t));
}
return 0;
}
| Time Limit: 15000MS | Memory Limit: 131072K | |
| Total Submissions: 23384 | Accepted: 10182 | |
| Case Time Limit: 5000MS | ||
Description
As more and more computers are equipped with dual core CPU, SetagLilb, the Chief Technology Officer of TinySoft Corporation, decided to update their famous product - SWODNIW.
The routine consists of N modules, and each of them should run in a certain core. The costs for all the routines to execute on two cores has been estimated. Let\'s define them as Ai and Bi. Meanwhile, M pairs of modules need to do some data-exchange. If they are running on the same core, then the cost of this action can be ignored. Otherwise, some extra cost are needed. You should arrange wisely to minimize the total cost.
Input
There are two integers in the first line of input data, N and M (1 ≤ N ≤ 20000, 1 ≤ M ≤ 200000) .
The next N lines, each contains two integer, Ai and Bi.
In the following M lines, each contains three integers: a, b, w. The meaning is that if module a and module b don\'t execute on the same core, you should pay extra w dollars for the data-exchange between them.
Output
Output only one integer, the minimum total cost.
Sample Input
3 1
1 10
2 10
10 3
2 3 1000
Sample Output
13
一个超级源点和一个超级汇点,源点连每个任务,每个任务连汇点,容量分别任务为在相应核心执行的花费。需要在一个核心内工作的任务之间连一条线,容量为相应的额外花费。

#pragma comment(linker, "/STACK:102400000,102400000") #include <iostream> #include <algorithm> #include <string.h> #include <vector> #include <map> #include <queue> #include <stdlib.h> using namespace std; // ALGORITHM_MAXFLOW_SAP -> #define ALGORITHM_MAXFLOW_SAP_MAXN 20010 #define ALGORITHM_MAXFLOW_SAP_MAXM 880010 #define ALGORITHM_MAXFLOW_SAP_INF 0x7FFFFFFF struct ALGORITHM_MAXFLOW_SAP_Node { int from, to, next; int cap; } ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_MAXM]; int ALGORITHM_MAXFLOW_SAP_tol; int ALGORITHM_MAXFLOW_SAP_head[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_dep[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_cur[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_S[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_que[ALGORITHM_MAXFLOW_SAP_MAXN]; int ALGORITHM_MAXFLOW_SAP_n; void ALGORITHM_MAXFLOW_SAP_clear() { ALGORITHM_MAXFLOW_SAP_tol = 0; memset(ALGORITHM_MAXFLOW_SAP_head, -1, sizeof(ALGORITHM_MAXFLOW_SAP_head)); } void ALGORITHM_MAXFLOW_SAP_addedge(int u, int v, int w) { ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].from = u; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].to = v; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].cap = w; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].next = ALGORITHM_MAXFLOW_SAP_head[u]; ALGORITHM_MAXFLOW_SAP_head[u] = ALGORITHM_MAXFLOW_SAP_tol++; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].from = v; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].to = u; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].cap = 0; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_tol].next = ALGORITHM_MAXFLOW_SAP_head[v]; ALGORITHM_MAXFLOW_SAP_head[v] = ALGORITHM_MAXFLOW_SAP_tol++; } void ALGORITHM_MAXFLOW_SAP_BFS(int start, int end) { memset(ALGORITHM_MAXFLOW_SAP_dep, -1, sizeof(ALGORITHM_MAXFLOW_SAP_dep)); memset(ALGORITHM_MAXFLOW_SAP_gap, 0, sizeof(ALGORITHM_MAXFLOW_SAP_gap)); ALGORITHM_MAXFLOW_SAP_gap[0] = 1; int front, rear; front = rear = 0; ALGORITHM_MAXFLOW_SAP_dep[end] = 0; ALGORITHM_MAXFLOW_SAP_que[rear++] = end; while (front != rear) { int u = ALGORITHM_MAXFLOW_SAP_que[front++]; if (front == ALGORITHM_MAXFLOW_SAP_MAXN) { front = 0; } for (int i = ALGORITHM_MAXFLOW_SAP_head[u]; i != -1; i = ALGORITHM_MAXFLOW_SAP_edge[i].next) { int v = ALGORITHM_MAXFLOW_SAP_edge[i].to; if (ALGORITHM_MAXFLOW_SAP_dep[v] != -1) { continue; } ALGORITHM_MAXFLOW_SAP_que[rear++] = v; if (rear == ALGORITHM_MAXFLOW_SAP_MAXN) { rear = 0; } ALGORITHM_MAXFLOW_SAP_dep[v] = ALGORITHM_MAXFLOW_SAP_dep[u] + 1; ++ALGORITHM_MAXFLOW_SAP_gap[ALGORITHM_MAXFLOW_SAP_dep[v]]; } } } int ALGORITHM_MAXFLOW_SAP_SAP(int start, int end) { int res = 0; ALGORITHM_MAXFLOW_SAP_BFS(start, end); int top = 0; memcpy(ALGORITHM_MAXFLOW_SAP_cur, ALGORITHM_MAXFLOW_SAP_head, sizeof(ALGORITHM_MAXFLOW_SAP_head)); int u = start; int i; while (ALGORITHM_MAXFLOW_SAP_dep[start] < ALGORITHM_MAXFLOW_SAP_n) { if (u == end) { int temp = ALGORITHM_MAXFLOW_SAP_INF; int inser; for (i = 0; i < top; i++) if (temp > ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap) { temp = ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap; inser = i; } for (i = 0; i < top; i++) { ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i]].cap -= temp; ALGORITHM_MAXFLOW_SAP_edge[ALGORITHM_MAXFLOW_SAP_S[i] ^ 1].cap +=
