数组和广义表

Posted 2020-08-15 KennyRom

1、数组

数组的特点：

     元素数目固定；下标有界。

数组的操作：

    按照下标进行读写。

 

2、数组的顺序表示和实现

因计算机的内存结构是一维的，因此用一维内存来表示多维数组，就必须按某种次序将数组元素排成一列序列，然后将这个线性序列存放在储存器中。

 

通常有两种顺序存储方式：

（1）行优先顺序——将数组元素按行排列

       在PASCAL、C语言中，数组就是按行优先顺序储存。

（2）列优先顺序——将数组按列向量排列。

       在FORTRAN语言中，数组就是按列优先顺序储存的。

 

3、矩阵的压缩储存

利用2维数组描述矩阵

 

特殊矩阵：

为了节省储存空间，矩阵进行压缩存储：即为多个相同的非零的元素值分配一个储存空间；对0元素不分配空间。

 

（1）对称矩阵

只需对对称矩阵中n(n+1)/2个元素进行储存表示

 

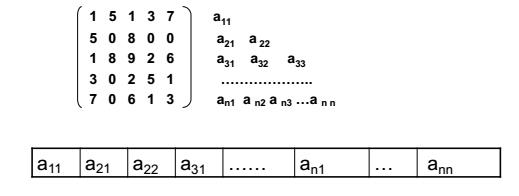
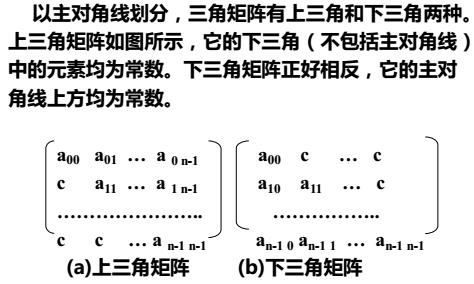
 （2）三角矩阵

 

 

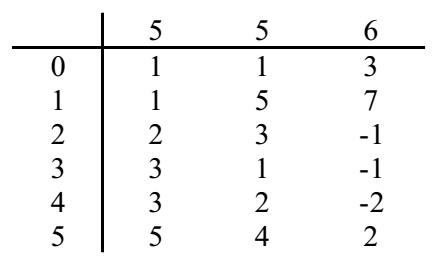
（3）稀疏矩阵

if 一个m*n的矩阵含有t个非零元素，且t远远小于m*n，则称这个矩阵为稀疏矩阵

 

利用三元组表示法对稀疏矩阵进行压缩储存

用三项内容表示稀疏矩阵中的每个非零元素，进行形式为：（i,j,value）

其中，i 表示行序号，j 表示列序号，value 表示非零元素的值

//稀疏矩阵，非零元素比较少
const int max=1000;

template<typename Object>
typedef struct
{
	int i, j;
	Object e;
}Triple;

template<typename Object>
typedef struct
{
	Triple<Object> data[max];
	int mu, nu, tu;
}TSMatrix;

　　

稀疏矩阵的转置

     转置前矩阵为M，转置后为T，M的列为T的行，因此，要按M.data的列序转置

所得到的转置矩阵T的三元组表必定按行优先存放

 

转置算法：

template<typename Object>
void trans( TSMattrix<Object>M, TSMatrix<Object>T)
{
    T,mu=M.nu;
    T.nu=M.mu;
    T.tu=M.tu;

   if(T.tu)
   {
       int q=0;
       for(int col=0; col< M.nu;col++)
           for(int p=0; p<M.tu; p++)
              {
                  if(M.data[p].j==col)
                    {
                         T.data[q].i=M.data[p].j;
			 T.data[q].j=M.data[p].i;
			 T.data[q].e=M.data[p].e;
			 q++;
                    }
              }
    }
}

　这个转置算法的时间复杂度为O(n*t)，效率太低了

 

快速转置算法

一遍扫描先确定三元组的位置关系，二次扫描由位置关系装入三元组

为了预先确定矩阵M中的每一列的第一个非零元素在数组B中应有的位置，需要闲球的矩阵M中的每一列中非零元素的个数。

为此，需要设计两个一位数组num[0...n-1]和cpot[1..n-1]

num[0...n-1]：统计M中每一列非零元素的个数

cpot[0...n-1]：由递推关系得出M中的每列第一个非零元素在B中的位置

cpot[col]=cpot[col-1]+num[col-1];

template<typename Object>
void fasttranstri( TSMatrix<Object> M, TSMatrix<Object>T)
{
    int q;
    int *num=new int[M.nu];
    int *copt=new int[M.nu];
    T.mu=M.nu;
    T.nu=M.mu;
    T.tu=M.tu;

    if(M.tu)
    {
        for(int col=0; col<M.nu ;col++)
            num[col]=0;

  
        //统计每列非零元素个数
        for(int k=0; col<M.tu; k++)
            ++num[m.data[k].j];

        //每列第一个非零元素在T中位置
        copt[0]=0;
        for(int col=1; col <M.nu;col++)
             copt[col]=copt[col-1]+num[col-1];

        for(int p=0; p<M.tu; p++)
       {
              int col=M.data[p].j;
	      q=cpot[col];
	      T.data[q].i=M.data[p].j;
	      T.data[q].j=M.data[p].i;
	      T.data[q].e=M.data[p].e;
	      ++copt[col];
       }
    }
    delete[] num;
    delete[] cpot;
}

　　时间复杂度为O(n+t)

 

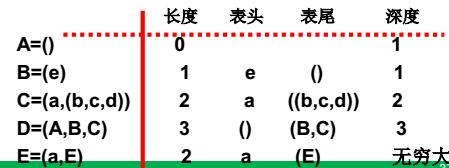
4、广义表的定义