python 基础 正则，递归 生成器

Posted 2020-06-14

  字符串是编程时涉及到的最多的一种数据结构，对字符串进行操作的需求几乎无处不在。比如判断一个字符串是否是合法的Email地址，虽然可以编程提取@前后的子串，再分别判断是否是单词和域名，但这样做不但麻烦，而且代码难以复用。

    正则表达式是一种用来匹配字符串的强有力的武器。它的设计思想是用一种描述性的语言来给字符串定义一个规则，凡是符合规则的字符串，我们就认为它“匹配”了，否则，该字符串就是不合法的。

    下面这张图展示了使用正则表达式匹配的流程

 

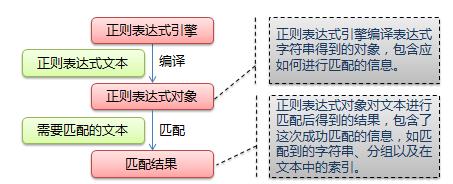
1、Python支持的正则表达式元字符和语法

语法	说明	表达式实例	完整匹配的字符串
字符
一般字符	匹配自己	abc	abc
.	匹配任意字符“\n”除外 DOTALL模式中（re.DOTALL）也能匹配换行符	a.b	abc或abc或a1c等
[...]	字符集[abc]表示a或b或c，也可以-表示一个范围如[a-d]表示a或b或c或d	a[bc]c	abc或adc
[^...]	非字符集，也就是非[]里的之外的字符	a[^bc]c	adc或aec等
预定义字符集（也可以系在字符集[...]中）
\d	数字：[0-9]	a\dc	a1c等
\D	非数字：[^0-9]或[^\d]	a\Dc	abc等
\s	空白字符：[<空格>\t\n\f\v]	a\sc	a b等
\S	非空白字符：[^s]	a\Sc	abc等
\w	字母数字（单词字符）[a-zA-Z0-9]	a\wc	abc或a1c等
\W	非字母数字（非单词字符）[^\w]	a\Wc	a.c或a_c等
数量词（用在字符或(...)分组之后）
*	匹配0个或多个前面的表达式。（注意包括0次）	abc*	ab或abcc等
+	匹配1个或多个前面的表达式。	abc+	abc或abcc等
?	匹配0个或1个前面的表达式。（注意包括0次）	abc?	ab或abc
{m}	匹配m个前面表达式（非贪婪）	abc{2}	abcc
{m,}	匹配至少m个前面表达式（m至无限次）	abc{2,}	abcc或abccc等
{m,n}	匹配m至n个前面的表达式	abc{1,2}	abc或abcc
边界匹配（不消耗待匹配字符中的字符）
^	匹配字符串开头，在多行模式中匹配每一行的开头	^abc	abc或abcd等
$	匹配字符串结尾，在多行模式中匹配每一行的结尾	abc$	abc或123abc等
\A	仅匹配字符串开头	\Aabc	abc或abcd等
\Z	仅匹配字符串结尾	abc\Z	abc或123abc等
\b	匹配一个单词边界，也就是指单词和空格间的位置。例如， ‘er\b‘ 可以匹配"never" 中的 ‘er‘，但不能匹配 "verb" 中的 ‘er‘。
\B	匹配非单词边界。‘er\B‘ 能匹配 "verb" 中的 ‘er‘，但不能匹配 "never" 中的 ‘er‘。
逻辑、分组
|	或左右表达式任意一个（短路）如果|没有在()中表示整个正则表达式（注意有括号和没括号的区别）	abc|def ab(c|d)ef	abc或def abcef或abdef
(...)	分组，可以用来引用，也可以括号内的被当做一组进行数量匹配后接数量词	(abc){2}a	abcabca
(?P<name>...)	分组别名，给分组起个名字，方便后面调用
\<number>	引用编号为<number>的分组匹配到的字符串（注意是配到的字符串不是分组表达式本身）	(\d)abc\1	1ab1或5ab5等
(?=name)	引用别名为name的分组匹配到的字符串（注意是配到的字符串不是分组表达式本身）	(?P<id>\d)abc(?P=id)	1ab1或5ab5等

 

2、数量词的贪婪模式与分贪婪模式

    正则表达式通常用于在文本中查找匹配的字符串。Python里数量词默认是贪婪的（在少数语言里也可能是默认非贪婪），总是尝试匹配尽可能多的字符；非贪婪的则相反，总是尝试匹配尽可能少的字符。例如：正则表达式"ab*"如果用于查找"abbbc"，将找到"abbb"。而如果使用非贪婪的数量词"ab*?"，将找到"a"。

 

3、python的re模块

Python通过re模块提供对正则表达式的支持。使用re的一般步骤是先将正则表达式的字符串形式编译为Pattern实例，然后使用Pattern实例处理文本并获得匹配结果（一个Match实例），最后使用Match实例获得信息，进行其他的操作。

 1 import re
 2  
 3 # 将正则表达式编译成Pattern对象
 4 pattern = re.compile(r‘hello‘)
 5  
 6 # 使用Pattern匹配文本，获得匹配结果，无法匹配时将返回None
 7 match = pattern.match(‘hello world!‘) 
 8  
 9 if match:
10     # 使用Match获得分组信息
11     print match.group()

执行结果

hello

当然也可以直接使用re的模块的方法时候直接传递正则表达式参数来完成

1 macth = re.match(‘hello‘, ‘hello world‘)
2 if match:
3     print match.group()

执行结果是一样的

 

4、re模块的常用方法

re.compile(strPattern[, flag])

    参数：

        strPattern：正则表达式

        flag：匹配模式，可选值有

            re.I(re.IGNORECASE): 忽略大小写（括号内是完整写法，下同）

            M(MULTILINE): 多行模式，改变‘^‘和‘$‘的行为（参见上图）

            S(DOTALL): 点任意匹配模式，改变‘.‘的行为

            L(LOCALE): 使预定字符类 \w \W \b \B \s \S 取决于当前区域设定

            U(UNICODE): 使预定字符类 \w \W \b \B \s \S \d \D 取决于unicode定义的字符属性

            X(VERBOSE): 详细模式。这个模式下正则表达式可以是多行，忽略空白字符，并可以加入注释。

    返回值：Pattern对象是一个编译好的正则表达式，通过Pattern提供的一系列方法可以对文本进行匹配查找

    以下的方法既可以是Pattern对象的实例方法也可以是re模块的方法，语法稍有不同

match(string[, pos[, endpos]]) | re.match(pattern, string[, flags])

    这个方法将从string的pos下标处起尝试匹配pattern；如果pattern结束时仍可匹配，则返回一个Match对象；如果匹配过程中pattern无法匹配，或者匹配未结束就已到达endpos，则返回None。

    pos和endpos的默认值分别为0和len(string)；re.match()无法指定这两个参数，参数flags用于编译pattern时指定匹配模式。

    注意：这个方法并不是完全匹配。当pattern结束时若string还有剩余字符，仍然视为成功。想要完全匹配，可以在表达式末尾加上边界匹配符‘$‘。 

    参数：

    string：要匹配的字符串

    pos：匹配的开始下标

    endpos：匹配的结束下标

    pattern：正则表达式

    flags：匹配模式

    返回值：如果匹配成功返回match对象，否则返回None

search(string[, pos[, endpos]]) | re.search(pattern, string[, flags])

    这个方法用于查找字符串中可以匹配成功的子串。从string的pos下标处起尝试匹配pattern，如果pattern结束时仍可匹配，则返回一个Match对象；若无法匹配，则将pos加1后重新尝试匹配；直到pos=endpos时仍无法匹配则返回None。

pos和endpos的默认值分别为0和len(string))；re.search()无法指定这两个参数，参数flags用于编译pattern时指定匹配模式。 

    参数：同match

    返回值：同match

 

    我们通过一个实例来看一下两个方法的区别

>>> import re
>>> s = ‘hello world‘
>>> print(re.match(‘ello‘, s))
None
>>> print(re.search(‘ello‘,s ))
<_sre.SRE_Match object; span=(1, 5), match=‘ello‘>
    说明：可以看到macth只匹配开头，开头不匹配，就不算匹配到，search则可以从中间，只要能有匹配到就算匹配
findall(string[, pos[, endpos]]) | re.findall(pattern, string[, flags])
    搜索string，以列表形式返回全部能匹配的子串。有点像search的扩展，把所有匹配的子串放到一个列表
    参数：同match
    返回值：所有匹配的子串，没有匹配则返回空列表
>>> import re             
>>> s = ‘one1two2three3four4‘
>>> re.findall(‘\d+‘, s)
[‘1‘, ‘2‘, ‘3‘, ‘4‘]

split(string[, maxsplit]) | re.split(pattern, string[, maxsplit]):

    按照匹配字子串将字符串进行分割，返回分割收的列表

    参数：

     string：要分割的字符串

     pattern：正则表达式

    maxsplit：最大分割次数

    返回值：分割后的列表

    实例

>>> import re                 
>>> s = ‘one1two2three3four4‘
>>> re.split(‘\d+‘, s)
[‘one‘, ‘two‘, ‘three‘, ‘four‘, ‘‘]

sub(repl, string[, count]) | re.sub(pattern, repl, string[, count])

    使用repl替换string中匹配的每一子串

    参数：

    repl：替换的字符串或方法，这里需要说一下这个方法，方法接收macth对象，方法的返回值作为替换的字符串，换句话就是经过处理的字符串。

    string：要进行替换的字符串

    pattern：正则表达式

    count：替换的次数

    实例：对于repl是个方法的情况，正好这次作业用到，用来替换多个则很难过福号的情况。假设我们有一个四则运算表达式 ‘--(1.1+1+1-(-1)-(1+1+(1+1+2.2)))+-----111+--++--3-+++++++---+---1+4+4/2+(1+3)*4.1+(2-1.1)*2/2*3‘，遵循奇数个负号等于正否则为负的原则进行替换，我们可以这样

 1 if __name__ == ‘__main__‘:
 2     import re
 3     s = ‘--(1.1+1+1-(-1)-(1+1+(1+1+2.2)))+-----111+--++--3-+++++++---+---1+4+4/2+(1+3)*4.1+(2-1.1)*2/2*3‘
 4     def replace_sign(expression):
 5         ‘‘‘
 6         替换多个连续+-符号的问题，例如+-----，遵循奇数个负号等于正否则为负的原则进行替换
 7         :param expression: 表达式，包括有括号的情况
 8         :return: 返回经过处理的表达式
 9         ‘‘‘
10         def re_sign(m):
11             if m:
12                 if m.group().count(‘-‘)%2 == 1:
13                     return ‘-‘
14                 else:
15                     return ‘+‘
16             else:
17                 return ‘‘
18         expression = re.sub(‘[\+\-]{2,}‘, re_sign, expression)
19         return expression
20  
21     s = replace_sign(s)
22     print(s)

 　　

1.迭代器&生成器

2.装饰器

　　　1.基本装饰器

　　　2.多参数装饰器(了解)

3.递归

4.算法基础：二分查找，二维数组转换，冒泡排序

5.正则表达式

 

 

迭代器&生成器

迭代器

迭代器是访问集合元素的一种方式。迭代器对象从集合的第一个元素开始访问，知道所有的元素都被访问结束。 迭代器只能往前不会后退， 另外，迭代器的一个大优点是不要求实现准备好整个迭代过程中所有的元素。迭代器仅仅在迭代到某个元素时才计算该元素。这个特性使 迭代器特别适用于便利一些巨大的或是无限的结合， 比如说几个G的日志文件。

 

特点：

1. 访问者不需要关心一个迭代器内部的结构，仅需要通过next()方法不断去取下一个内容

2.不能随机访问集合中的某个值，只能从头到尾依次访问

3.访问时不能回退

4.便于循环比较大的数据集合，节省内存。

生成一个迭代器如下：

 View Code

注：迭代器不能随意访问集合中的某一个值，只能从头到尾依次访问，且访问时不能回退

生成器generator：

定义：一个函数调用时返回一个迭代器，那这个函数就叫生成器(generator),如果函数中包含yield语法，那这个函数就会变成生成器。

代码如下：

 View Code

作用:这个yield的主要效果，就是可以中断函数运行状态，并保持中断状态，中断后， 代码可以继续往下执行，过一段时间后，还可以重新调用这个函数，从上次yield的下一句开始执行。

另外， 还可以通过yield实现在单线程的情况下实现并发运算的效果(实现异步)：

代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

import time def consumer(name):     print(‘%s 要吃包子了‘%name)     while True:         baozi = yield         print(‘%s 包子来了,包子要被%s 吃掉了‘%(baozi,name)) def producer(name):     C = consumer(‘A‘)     C1 = consumer(‘B‘)     C.__next__()     C1.__next__()     print(‘我要开始做包子啦‘)     for i in range(10):         time.sleep(1)         print(‘%s 做了两个包子‘%name)         C.send(i)         C1.send(i) producer(‘test‘)

装饰器：

python装饰器见另一片文档。

 

递归

特点

递归算法是一种直接或者间接地调用自身方法的过程，它往往使算法的描述简介而且易于理解。

递归算法解决问题的特点：：

(1) 递归就是在过程或函数里调用自身。

(2)在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口

(3)递归算法截图通常显得很间接，但递归算法结题的运行效率极低，所以一般都不提倡用递归算法设计程序。

　　　在递归调用的过程当中系统为每一层的返回点、局部变量等开辟了栈来存储。递归次数过程容易造成栈溢出等， 所以一般都提倡用递归算法设计程序。

要求

递归算法所体现的“重复” 一般有三个要求：

一是每次调用都在规模上都有所缩小(通常都是减半)

二是相邻两次重复之间有紧密的联系， 前一次要为后一次做准备(通常前一次的输出是为后一次的输入做铺垫)

三是在问题的规模极小时而不再进行递归调用，因而每次递归调用都是有条件的， 无条件出口的递归调用最后会陷入死循环。

示例代码如下：

在数据量比较大的情况下通过二分法查找某个数据

def searchdate(data_result,find_n):
    mid = int(len(data_result)/2)
    if len(data_result) >1:
        if find_n < data_result[mid]:
            print(‘find_n in [mid] left‘)
            searchdate(data_result[:mid],find_n)
        elif find_n > data_result[mid]:
            print(‘find_n in [mid] right‘)
            searchdate(data_result[mid:],find_n)
        else:
            print(‘find date in data_result [%s]‘ %data_result[mid])
if __name__ == ‘__main__‘:
    dabc = list(range(1,99999))
    searchdate(dabc,57668)

通过二分算法我们可以很快的实现数据查找， 特别是在数据量比较大的情况下， 效果会更好。

算法基础

1.生成一个4*4的二维数组并将其瞬时旋转90度

# 生成一个二维数组
date = [[aaa for aaa in range(4)] for bbb in range(4)]
name = ‘打印‘
result = name.center(30, ‘*‘)
for i in date:
    print(i)
for r_index, row in enumerate(date):  # 循环遍历数组，并获取第一层的数组下标
    for c_index in range(r_index, len(row)):  # 根据第一层的下标，获取第二层
        tmp = date[c_index][r_index]  # 将要交换的元素先存到临时变量中
        date[c_index][r_index] = row[c_index]  # 元素交换
        date[r_index][c_index] = tmp
print(result)

for r in date:
    print(r)

##################另外一种写法##################

data = [[aaa for aaa in range(4)] for bbb in range(4)]
for i in range(data.__len__()):
    for k in range(data.__len__()):
        if (i>k):
            temp = data[i][k]
            data[i][k]= data[k][i]
            data[k][i]=temp

for i in data:
    print(i)

ps:对于第一种写法目前还是不太能理解，后期需要在看一遍视频，加深一下

2. 斐波那契数列算法：

简单的来说斐波那契数列就是第三个数值等于第一个数值+第二个数值之和，如下：

1 2 3 5 8 13 21 34 ....

示例代码如下：

def calr(arg1,arg2,stop):
    if arg1 == 0:
        print(arg1,arg2)
    arg3 = arg1 + arg2
    print(arg3)
    if arg3 <stop:
        calr(arg2,arg3,stop)

calr(0,1,789)

3.冒泡排序

将一个不规则的数组按从小到大的顺序进行排序

代码如下:

data = [10,4,33,21,54,3,8,11,5,22,2,1,17,13,6]
 
print("before sort:",data)
 
previous = data[0]
for j in range(len(data)):
    tmp = 0
    for i in range(len(data)-1):
        if data[i] > data[i+1]:
            tmp=data[i]
            data[i] = data[i+1]
            data[i+1] = tmp
    print(data)
 
print("after sort:",data)


################另外一种写法###################

data = [11, 1231, 124, 24123, 554, 632, 591, 112, 109, 889, 100]
print(‘before sort:‘, data)
for i in range(len(data)):
    for k in range(i):
        if data[i] < data[k + 1]:
            data[i], data[k + 1] = data[k + 1], data[i]
print(‘after sort:‘, data)