图论-强连通分量-Tarjan算法

Posted 2020-08-14 xqmmcqs

有关概念：

　　如果图中两个结点可以相互通达，则称两个结点强连通。

　　如果有向图G的每两个结点都强连通，称G是一个强连通图。

　　有向图的极大强连通子图（没有被其他强连通子图包含），称为强连通分量。（这个定义在百科上和别的大神的博客中不太一样，暂且采用百科上的定义）

　　Tarjan算法的功能就是求有向图中的强连通分量

思路：

　　定义DFN_i存放访问到i结点的次序（时间戳），Low_i存放i结点及向i下方深搜到的结点中能追溯到的访问次序最小的结点的访问次序（即这些结点回溯上去能找到的最小的DFN值），找到未被访问过的结点时进栈，当找到一个强连通分量的根结点时（判断条件DFN_i==Low_i），将该结点到栈顶之间的元素退栈，作为一个强连通分量

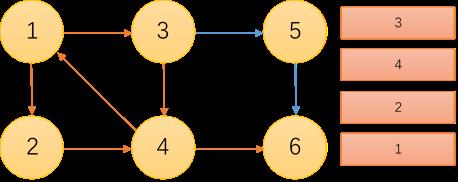
　　从结点1开始，枚举每一个未被访问的结点，以该节点为点u，进栈，赋DFN_u=Low_u=time++，枚举每一个以u为起点的边，找到指向的终点v，进行判断：

　　（1）v未被访问过，则以v为起点继续深搜，并做Low_u=min(Low_u,Low_v)；

　　（2）v仍在栈内，则做Low_u=min(Low_u,DFN_v)；（如果v的访问次序更小，更新Low_u，在回溯时更新u的父结点的Low值）

　　枚举完毕后，判断该结点是否为某一强连通分量的根节点，是则进行退栈操作

样例推导：

从1开始深搜，1、2、4依次进栈

DFN={1,2,0,3,0,0}

搜索到4时有指向1的一条边，Low₄=DFN₁=1

6进栈

DFN={1,2,0,3,0,4}

判定 DFN₆==Low₆，6为第一个强连通分量的根节点，从6向栈顶（其实就一个元素）退栈，得第一个强连通分量为{6}

回溯到1，并更新Low值

DFN={1,2,0,3,0,4}

Low={1,1,0,1,0,4}

继续深搜到3，又有一条边指向4，Low₃=DFN₄=3

5进栈，有一条边指向6，但6被访问过且不在栈内，pass

此时5满足条件出栈，第二个强连通分量为{5}

回溯到1，更新Low值

DFN={1,2,5,3,6,4}

Low={1,1,3,1,6,4}

最后1满足条件，从1到栈顶出栈，第三个强连通分量为{1,2,3,4}

复杂度：

　　每一个点和边均只被访问过一次，时间复杂度为O(n+m)

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 using namespace std;
 5 #define MAXN 
 6 #define MAXM 
 7 int n,m,time,cnt,heads[MAXN],DFN[MAXN],Low[MAXN],stack[MAXN],top,belong[MAXN];//time为访问次序，belong存该结点属于第几个强连通分量 
 8 bool vis[MAXN];//该结点是否在栈内 
 9 struct node
10 {
11     int v,next;
12 }edge[MAXM];
13 void add(int x,int y)
14 {
15     edge[++cnt].next=heads[x];
16     heads[x]=cnt;
17     edge[cnt].v=y;
18 }
19 void tarjan(int u)
20 {
21     DFN[u]=Low[u]=++time;
22     vis[u]=true;
23     stack[++top]=u;//进栈 
24     for(int i=heads[u];i!=0;i=edge[i].next)
25     {
26         int v=edge[i].v;
27         if(!DFN[v])//是否被访问过，DFN初值都为0，只有访问过才会被赋值 
28         {
29             tarjan(v);
30             Low[u]=min(Low[u],Low[v]);
31         }
32         else if(vis[v])Low[u]=min(Low[u],DFN[v]);
33     }
34     if(DFN[u]==Low[u])//该结点为根结点，出栈 
35     {
36         int i;
37         cnt++;
38         do
39         {
40             i=stack[top--];
41             vis[i]=false;
42             belong[i]=cnt;
43             print();//输出之类的操作 
44         }while(u!=i);
45     }
46 }
47 int main()
48 {
49     scanf("%d%d",&n,&m);
50     for(int i=1;i<=m;i++)
51     {
52         int x,y;
53         scanf("%d%d",&x,&y);
54         add(x,y);//默认输入有向边 
55     }
56     cnt=0;//cnt为强连通分量数量 
57     for(int i=1;i<=n;i++)
58         if(!DFN[i])tarjan(i);
59     return 0;
60 }

*参考：http://baike.baidu.com/link?url=3xvU8jjqA2McnNL07G_5XHs8so96ZLAwjmc5oMPY1K67EkixIzyHdrn6QhqCsM9da0SVN_9vvca4iEcXJMyRVK

http://blog.sina.com.cn/s/blog_69a101130100k1cm.html

http://blog.sina.com.cn/s/blog_691ce2b701016u53.html