论文学习-sparse methods for direction of arrival estimation1.
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文学习-sparse methods for direction of arrival estimation1.相关的知识,希望对你有一定的参考价值。
翻译自Sparse Methods for Direction-of-Arrival Estimation(Zai Yang∗†, Jian Li‡, Petre Stoica§, and Lihua Xie†)
direction of arrival(DOA)
1.引言
DOA(direction of arrival)estimation指接收一些电磁波的方向信息的过程,这些电磁波来自许多形成阵列传感器的接收雷达的输出。
传统的波束形成器(beamformer)仅仅使用了对空间采样数据的傅立叶光谱分析,后来被用于提高紧密排列数据的估计【1】。Pisarenko发现DOA可以从二阶统计数据中恢复【2】,基于子空间的方法得到发展,比如MUSIC(multiple signal classification)【3-7】,具体方法可见【8-9】。这些方法都需要满足一定条件,如beamformer是基于协方差(convariance-based)并且需要许多数据快照来正确估计数据协方差矩阵。而且,他们对source correlation 很敏感因此很容易因此秩亏(rank deficiency)。
这些方法是由稀疏表示和压缩感知方法得出【10-14】,稀疏估计算法可用于在不知道信号数据数目、有限的快拍数据和高度相关信号等方面。
稀疏表示用于离散线性系统,而DOA参数是连续的且观测数据是非线性的。我们将sparse methods for DOA estimation 分为三类-网格on-grid、非网格off-grid、无网格gridless。
本文符号说明:
R、C分别表示实数和复数
|.|表示一个标量振幅或集合的基数。
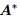 :复共轭、伴随矩阵(complex conjugate)
:复共轭、伴随矩阵(complex conjugate)
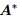 :共轭转置(conjugate transpose)
:共轭转置(conjugate transpose)
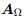 :A 的子矩阵(rows indexed by the set omiga)
:A 的子矩阵(rows indexed by the set omiga)
Tr(A):trace of A
E[.]:期望
2.DATA MODEL
2.1 DATA MODEL
sk (t)为窄带远场源信号,撞击来自方向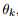 的阵列的全方位传感器,不同传感器的延时可以表示为相移,由此推出公式1:
的阵列的全方位传感器,不同传感器的延时可以表示为相移,由此推出公式1:
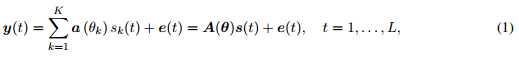
y(t)是阵列输出,且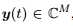 ,M是传感器数目(K<M),e(t)是测量噪声。
,M是传感器数目(K<M),e(t)是测量噪声。
 是第k个信号的矢量方向,其由传感器阵列的几何形状确定,
是第k个信号的矢量方向,其由传感器阵列的几何形状确定,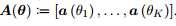
于是,公式1可以写为
2.2 THE ROLE OF ARRAY GEOMETRY
建立极坐标,传感器坐标为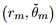 ,为方便起见,传感器间距离为波长的一半
,为方便起见,传感器间距离为波长的一半
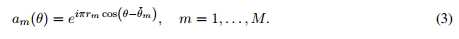
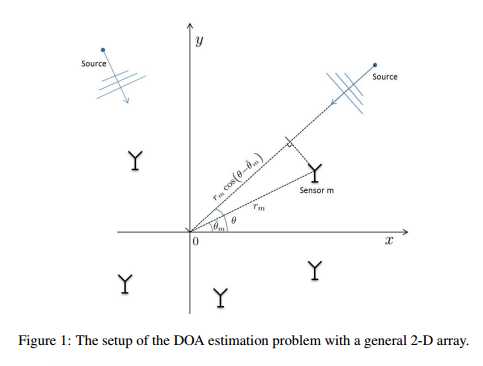
特殊地,若阵列是线性的,假设传感器在x轴上,即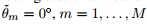 ,则
,则
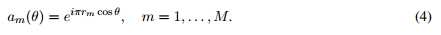
通过定义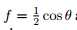 ,则
,则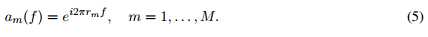
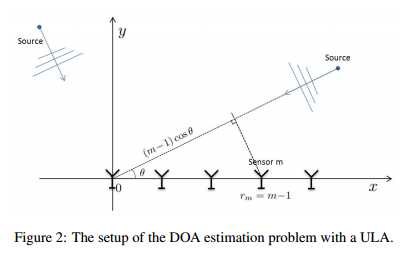
在单个快拍数据的情况下,空间DOA问题就成了时间频率估计问题。如果我们进一步假设线性阵列传感器是均等排列的,那么阵列就是ULA(uniform linear array)。考虑阵列的两个相邻天线以波长的一半排列,那么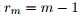 ,即
,即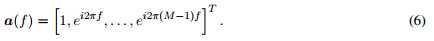
如果只保留ULA的部分传感器,则为SLA(sparse linear array).
2.3 PARAMETER IDENTIFIBALITY
保证参数唯一识别是正确估计的首要条件【15-ULA】【16-20】,对一个普通阵列,我们定义
定义spark(A):A中元素的最小数量是线性相关的,即
定理2.1:当且仅当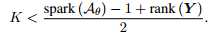 ,任何K信号可以由
,任何K信号可以由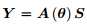 唯一得出【19】
唯一得出【19】
在当个快拍数据的情况下,定理2.1即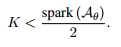
由定理2.1可知,更多快拍数据意味着更多源可以被确定,除非信号源有相同的比例因子。
在ULA情况下,定理2.1即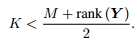
由rank(s)<=K和公式8,可得
【16】指出如果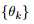 是固定的,S是连续值,那么K信号可以被唯一确定
是固定的,S是连续值,那么K信号可以被唯一确定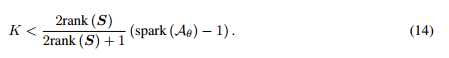
3.SPARSE REPRESENTATION AND DOA ESTIMATION
3.1 SPARSE REPRESENTATION AND COMPRESSED SENSING
3.1.1 PROBLEM FORMULATION
定义
其中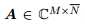 是给定矩阵,
是给定矩阵,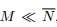 ;
;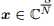 是稀疏系数,e是表征误差(representation error),因此y由公式1可被A中的K atoms的线性组合近似表示,这说明多维数据可以被维数较低的子空间近似表示(K<M)。于是,我们的目标就是找到向量x。
是稀疏系数,e是表征误差(representation error),因此y由公式1可被A中的K atoms的线性组合近似表示,这说明多维数据可以被维数较低的子空间近似表示(K<M)。于是,我们的目标就是找到向量x。
在压缩传感中,x是通过欠定线性系统(underdetermined得到的稀疏信号(of interest??)【16】。给定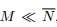 ,已知信号y指压缩数据,A是给定的传感矩阵。稀疏表示和压缩传感比较类似。
,已知信号y指压缩数据,A是给定的传感矩阵。稀疏表示和压缩传感比较类似。
我们需首先解决下面的优化问题
在没有噪声的情况下

其中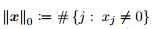 指x中的非零项,即伪范数l0或x的稀疏性。
指x中的非零项,即伪范数l0或x的稀疏性。
因此如果x的稀疏性满足
稀疏信号x可由公式17确定,这和定理2.1的公式很相似。
但该最优问很难求解,比较好的方法如l1最优【10,11】、lq伪范数优化【26-32】、贪婪算法如OMP、SP【33-38】,最大似然估计MLE(maximun likelihood estimation) 等。
3.1.2 convex relaxation(BP)

由于l1范数是凸的(convex),公式19可以通过多项式求解(实际上,这一方法源自【41】的地震数据恢复)。
定义矩阵A的互相关为A的任两列的最大绝对相关:
很明显,如果A 的两项高度相关,那么他们对y的贡献很难辨别,因此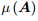 必须很小。
必须很小。
定理3.1【11】假设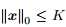 ,
,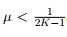 ,那么x可被唯一确定
,那么x可被唯一确定
定义【42】矩阵A的k-限制等距常数(RIC)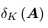 最小使得所有k-稀疏向量都满足不等式
最小使得所有k-稀疏向量都满足不等式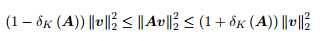
定理3.2【43】 假设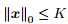 ,
,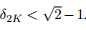 ,那么x可被唯一确定
,那么x可被唯一确定
使用RIP能获得比互相关更好的结果,但计算更复杂
在有噪声的情况下:
LASSO 【46】(least absolute shrinkage and selection operator) 
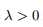
BPDN(basic pursuit denoising) 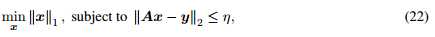
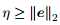
SR-LASSO【47】(square-root lasso):
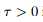
LASSO假设噪声为高斯分布,参数 namda 与噪声的标准偏差成比例,SR-LASSO的假设更弱,参数选择可以与噪声无关。
如上所述的l1优化问题是凸的并且可以用多项式求解,但是如果问题维度太高则效率较低因为l1范数不是一个光滑函数。更好的方法比如l1-magic【48】、内点法【49】、共轭梯度法【50】、不动点延拓法(continuation)【51】、ADMM等等。
3.1.3 lq optimization

FOCUSS【26-27】(focal underdetermined system solver):一种迭代加权最小二乘法,每次迭代中,FOCUSS解决下面的加权最小二乘问题: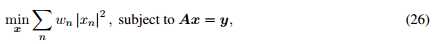
其中权重系数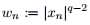 通过最新的x更新,这一方法即优化-最小化(MM)
通过最新的x更新,这一方法即优化-最小化(MM)
在有噪声的情况下,公式27可代替公式21:【28】

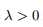
namda 的参数估计很麻烦,故使用一种最大后验(MAP:maximum a posterior)估计方法--SLIM(sparse learning via iterative minimization)【32】
x的先验分布:
【先验分布:任一未知量x都可看作随机变量,可用一个概率分布区描述,这个分布称为先验分布
后验分布:在获得样本之后,总体分布、样本与先验分布通过贝叶斯公式结合起来得到一个关于未知量x新的分布,即后验分布。它集中了总体、样本和先验中有关x的一切信息,而又排除了一切与x无关的信息
贝叶斯公式:![]()
任何关于x 的统计推断都应该基于x的后验分布进行。】
SLIM通过处理下面的lq优化问题来计算MAP: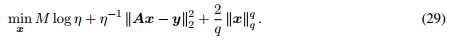
为计算公式29,SLIM像FOCUSS一样更新x。但是,SLIM基于最新的x更新高斯噪声变量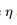 。一旦q给定,SLIM 便是 hyper-parameter free(超参数 free??)
。一旦q给定,SLIM 便是 hyper-parameter free(超参数 free??)
3.1.4 maximum likehood estimation(MLE)
MLE的优点是不需要知道噪声和稀疏程度。假设x 为均值为0、协方差为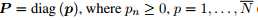 的多元高斯分布(变量),高斯噪声变量为
的多元高斯分布(变量),高斯噪声变量为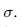
联系公式16中服从均值为0,协方差为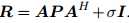 的y,负的对数似然函数为
的y,负的对数似然函数为
参数p、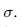 可通过最小化公式30 估计得到
可通过最小化公式30 估计得到 
于是稀疏信号x的后验分布为
由于实际上p的大多数项接近0,公式31的全局优化和l0优化一致。【57】
MLE的主要困难是计算公式31,其第一项是非凸的。更好的方法有加权优化【58】、稀疏贝叶斯学习(SBL)【57、59-60】
3.2 sparse representation and DOA estimation :the link and the gap
比较公式1和公式16
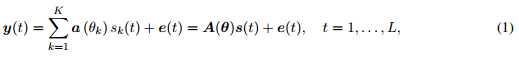

DOA估计的过程可归结于数据快拍的稀疏表示,然而两者之间有许多区别。首先,稀疏表示的项是有限的,由矩阵给出,而DOA估计的参数是连续的,即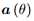 由连续参数 theta 参数化,有无限多项。其次,DOA估计由许多snapshots,而稀疏表示只有单个,因此挖掘DOA估计中的时间冗余是很重要的,因为天线的数目会受限制于物理和其他因素。最后,稀疏表示所使用的技术是基于不相干分析的,而DOA估计的项是完全相关的。
由连续参数 theta 参数化,有无限多项。其次,DOA估计由许多snapshots,而稀疏表示只有单个,因此挖掘DOA估计中的时间冗余是很重要的,因为天线的数目会受限制于物理和其他因素。最后,稀疏表示所使用的技术是基于不相干分析的,而DOA估计的项是完全相关的。
接下来的三章描述了解决第一个gap的三种不同方法。
4. ON-GRID SPARSE METHODS
主要问题是如何找出multiple snpshots 的时间冗余。
4.1 DATA MODEL
以一系列网格点来代替DOA域:
网格大小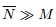 ,由此可得
,由此可得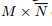 矩阵:
矩阵: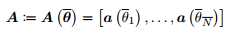
公式2可写为:
其中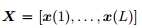 是一个
是一个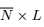 的矩阵,且
的矩阵,且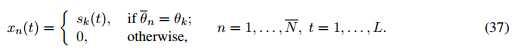
很明显,x(t)只包含K个非零项,对应于K DOAs,由于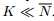 ,其为稀疏向量,即X是行稀疏的。
,其为稀疏向量,即X是行稀疏的。
公式16和公式36的唯一区别是公式36包含multiple snapshots或者说multiple measurements vetcors(MMVs)。在单个快拍数据(SMV)的情况下(L=1),稀疏表示可以应用于DOA估计,在多个快拍数据的情况下,主要困难是如何找出multiple snpshots 的时间冗余。
4.2 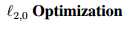
因为X的每一行对应于一个潜在的源,我们可以定义稀疏性为X非零行的数目,如下:【18 75】
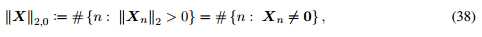
Xn表示X的第n行,注意公式38中的l2范数可以用别的代替。仿照单快拍数据的l0优化,l2,0优化可以在没有噪声的情况下推出: 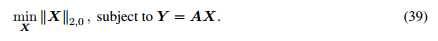
假设可以得到最优解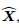
定理4.1【18】 如果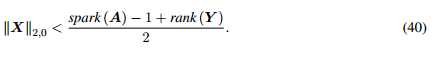
公式40和公式10很相似。由定理4.1,更多的快拍数据则rank(K)增加,可恢复的DOAs数目也会增加。除非y(t)有相同的比例因子。很不幸,和单快拍数据一样,上述方法很难实现。
4.3 Convex Relaxation
4.3.1 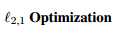

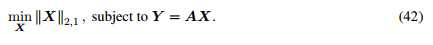
同公式21、22,在噪声存在的情况下,我们可以解LASSO问题: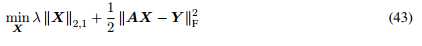
及BPDN问题: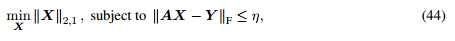
参数的选择是很困难的,给定参数变量,ULA\\SLA【81-83】提供了方法。
4.3.2 dimensionality reduction via l2,1 - SVD 【67】
通过只保存K维信号子空间将快拍数据的数目从L降到K
奇异值分解:
 M*K维矩阵,
M*K维矩阵,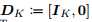
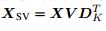
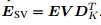
则
公式47和公式36相似,但降维了。所以l2,1优化问题(l2,1-SVD)可以转化为公式43、44。
然而,参数调节(公式43、44中的namda,)仍然是一个难题。
4.3.3 Another Dimensionality Reduction Techique
另一种将快拍数据的数目从L降到M的方法,和l2,1由相同的运行效果【84】。通过保存信号和噪声的子空间,Y的秩r<=M,从而得到:
其保存了所有的data power,因为Y只有r个非零奇异值
类似地,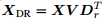
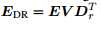
则
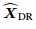 是下述LASSO问题的解:
是下述LASSO问题的解: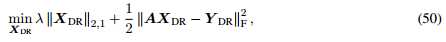
那么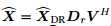 为公式43的解,注意到
为公式43的解,注意到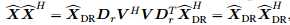 ,其对角线为行的能量(power),即
,其对角线为行的能量(power),即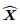 和
和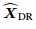 的行能量相等,两者是相等的。
的行能量相等,两者是相等的。
证明:令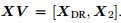
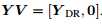
其中V为酉矩阵(n阶复方阵U的n个列向量是U空间的一个标准正交基,又称幺正矩阵)
很明显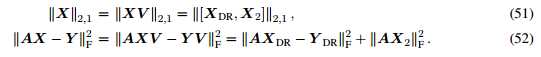
即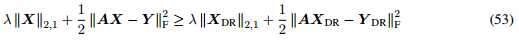
上式等号成立当且仅当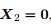 或
或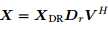
降维法之所以比l2,1-SVD好是因为参数可以像l2,1优化一样被调整,一旦噪声给定,解就是可行的。
4.4 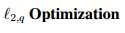
对比3.1.3中lq范数的定义,我们可以定义l2,q来找出X的稀疏:
对比公式42、43,在没有噪声的情况下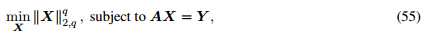
在有噪声的情况下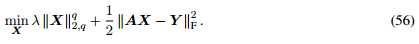
公式55:单快拍数据的情况下,M-FOCUSS算法【66】可用于求解下列加权最小二乘问题
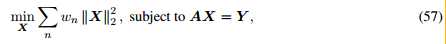
公式56类似求解。
为避免公式56中调整参数的问题,SLIM【32】
X的先验分布:
X的最大后验: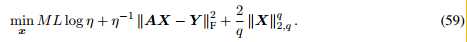
通过使用M-FOCUSS,我们可以迭代地更新X和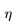 in closed form,得到SLIM的多个快照版本(multiple snapshot version)
in closed form,得到SLIM的多个快照版本(multiple snapshot version)
4.5 sparse iterative covariance-based estimation (SPICE):基于稀疏迭代协方差估计
假设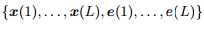 是互不相关的,并且
是互不相关的,并且
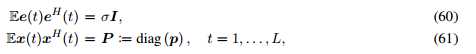
其中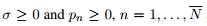 (注意下面的推导也可用于异方差噪声
(注意下面的推导也可用于异方差噪声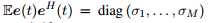 ) ,因此
) ,因此 也是互不相关的,其协方差矩阵为:
也是互不相关的,其协方差矩阵为:
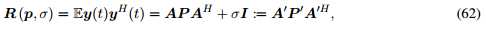
其中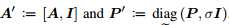
令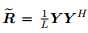 ,将其矢量化使得
,将其矢量化使得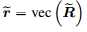
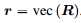
因为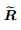 协方差矩阵的无偏估计,所以
协方差矩阵的无偏估计,所以
且
tip
【kronecker product
 】
】
由【85 86】
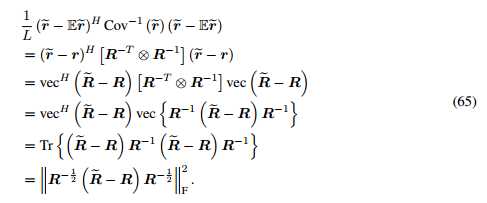
突然出bug了,这篇先写到这,另写一篇。
以上是关于论文学习-sparse methods for direction of arrival estimation1.的主要内容,如果未能解决你的问题,请参考以下文章