抽奖算法-指定概率的随机

Posted 2020-08-14 Look Into Coding

 

抽奖模型

普通概率模型

普通概率模型是最常用的一种模型，但是在游戏运营过程中的确发现很多小白玩家不能正确理解——他们认为中奖率 10% 的设定等同于抽 10 次肯定会中一次。这显然是错误的，普通概率模型的中奖抽奖次数是基于正态分布的，而且每次抽奖的事件是独立的，并不会因为你前面抽了 9 次没中奖，第十次就一定能中奖。

虽然在大量的统计中，两次中奖的平均间隔是 10 次，但是还有一个有趣的数据是连续 10 次都没中奖的概率约为 (1-10%)^10 ~= 34.8% 可不小呢。

此外「标准差」是一个很有意思的数据，经过模拟统计，10% 中奖率得到的标准差为 9.62 ——也就是说绝大分部人经过 10 ± 9.62 次抽奖即能中奖，运气再背抽 20 次也差不多能得到奖励了。

这种概率模型能非常准确地实现策划的需求，但是会惹来一些小白玩家的差评——为什么你说中奖率是 10% 但是我抽了 20 次还没有中奖！然后给你打个一星。所以很多游戏运营商为了顾及玩家的体验，会对普通概率模型进行修订，增设一些保底抽奖次数，例如每第 10 次固定中奖（10，20，30...）

对于这种做法，我暂不于评价。但是让我们看看如果硬生生地加入固定中奖的设定，会给数值带来什么变化吧。

固定中奖模型

每次抽奖中奖率依旧为 10% ，但每第十次抽奖必中。

这时候玩家得到的抽奖体验是：10 次抽奖肯定能中奖，而且不止中一次，爽暴了是不是。实际期望高达 19% 这远远超出策划 10% 的预期。所以策划琢磨着不能便宜了玩家，只能把中奖率调低。但是这会导致中奖集中在每 10 次附近，抽奖的乐趣几近丧失。

这样看来，固定中奖模型是否真的无药可救？其实还是有可以优化的地方。

计数器模型

每次抽奖中奖率依旧为 10% ，若连续 9 次未中奖，下一次抽奖必中奖。

这个需求看起来和上面好像没什么不同，但是保底的条件不再是每第 10 次，而是发生在每连续 9 次未中奖后。也就是说计数器会在每次中奖后清 0 重计。

 

随机步长累加模型

也是一种保底中奖模型，只不过去掉了独立随机事件，并把计数增长改为随机量，最终在累计超过阈值时得奖。这种模型如果有个较大的阈值和较小的步长下限，还可以起到让玩家在头几次抽奖必然不中（大）奖的效果。另外在这种模型下，计数器甚至可以对玩家可见，让看玩家看到进度和目标，感受到奖励是可达的、近在眼前的。

 

 

 

 

抽奖算法

/// <summary>
/// 抽奖
/// </summary>
public class Prize
{
    /// <summary>
    /// 奖品关键字
    /// </summary>
    public string Key { get; set; }

    /// <summary>
    /// 权重/数量
    /// </summary>
    public int Poll { get; set; }


    /// <summary>
    /// 中奖区间
    /// </summary>
    class Area
    {
        /// <summary>
        /// 奖品关键字
        /// </summary>
        public string Key { get; set; }

        /// <summary>
        /// 开始索引位置
        /// </summary>
        public int Start { get; set; }

        /// <summary>
        /// 截止索引位置
        /// </summary>
        public int Over { get; set; }
    }

    /// <summary>
    /// 随机种子
    /// </summary>
    static Random Rand = new Random((int)DateTime.Now.Ticks);


    /// <summary>
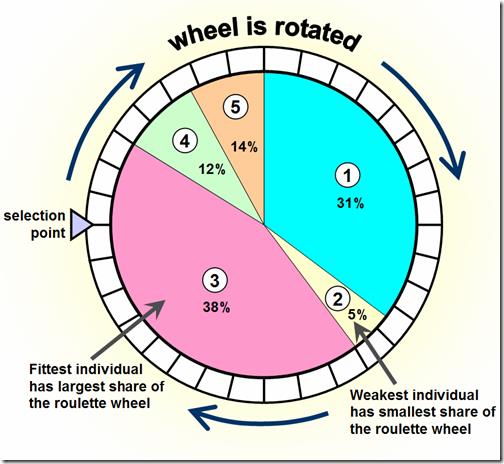
    /// 轮盘抽奖，权重值(在轮盘中占的面积大小)为中奖几率
    /// </summary>
    /// <param name="prizeList">礼品列表（如果不是百分百中奖则轮空需要加入到列表里面）</param>
    /// <returns></returns>
    public static string Roulette(List<Prize> prizeList)
    {
        if (prizeList == null || prizeList.Count == 0) return string.Empty;
        if (prizeList.Any(x => x.Poll < 1)) throw new ArgumentOutOfRangeException("poll权重值不能小于1");
        if (prizeList.Count == 1) return prizeList[0].Key; //只有一种礼品

        Int32 total = prizeList.Sum(x => x.Poll); //权重和               
        if (total > 1000) throw new ArgumentOutOfRangeException("poll权重和不能大于1000"); //数组存储空间的限制。最多一千种奖品（及每种奖品的权重值都是1）

        List<int> speed = new List<int>(); //随机种子
        for (int i = 0; i < total; i++) speed.Add(i);

        int pos = 0;
        Dictionary<int, string> box = new Dictionary<int, string>();
        foreach (Prize p in prizeList)
        {
            for (int c = 0; c < p.Poll; c++) //权重越大所占的面积份数就越多
            {
                pos = Prize.Rand.Next(speed.Count); //取随机种子坐标
                box[speed[pos]] = p.Key; //乱序 礼品放入索引是speed[pos]的箱子里面
                speed.RemoveAt(pos); //移除已抽取的箱子索引号
            }
        }
        return box[Prize.Rand.Next(total)];
    }

    /// <summary>
    /// 奖盒抽奖，每个参与者对应一个奖盒，多少人参与就有多少奖盒
    /// </summary>
    /// <param name="prizeList">礼品列表</param>
    /// <param name="peopleCount">参与人数</param>
    /// <returns></returns>
    public static string LunkyBox(List<Prize> prizeList, int peopleCount)
    {
        if (prizeList == null || prizeList.Count == 0) return string.Empty;
        if (prizeList.Any(x => x.Poll < 1)) throw new ArgumentOutOfRangeException("poll礼品数量不能小于1个");
        if (peopleCount < 1) throw new ArgumentOutOfRangeException("参数人数不能小于1人");
        if (prizeList.Count == 1 && peopleCount <= prizeList[0].Poll) return prizeList[0].Key; //只有一种礼品且礼品数量大于等于参与人数

        int pos = 0;
        List<Area> box = new List<Area>();
        foreach (Prize p in prizeList)
        {
            box.Add(new Area() { Key = p.Key, Start = pos, Over = pos + p.Poll }); //把礼品放入奖盒区间
            pos = pos + p.Poll;
        }

        int total = prizeList.Sum(x => x.Poll); //礼品总数
        int speed = Math.Max(total, peopleCount); //取礼品总数和参数总人数中的最大值

        pos = Prize.Rand.Next(speed);
        Area a = box.FirstOrDefault(x => pos >= x.Start && pos < x.Over); //查找索引在奖盒中对应礼品的位置

        return a == null ? string.Empty : a.Key;
    }

}


/*
List<Prize> prizes = new List<Prize>();
prizes.Add(new Prize() { Key = "电脑", Poll = 1 });
prizes.Add(new Prize() { Key = "机柜", Poll = 2 });
prizes.Add(new Prize() { Key = "鼠标", Poll = 3 });
                        

string lp1 = Prize.LunkyBox(prizes, 6);
Console.WriteLine(lp1);


prizes.Add(new Prize() { Key = "谢谢惠顾", Poll = 5 });
string lp2 = Prize.Roulette(prizes);      
Console.WriteLine(lp2);
*/

 

 

参考

Return random `list` item by its `weight`

不同概率模型的抽奖体验

抽奖算法

一个简单抽奖算法的实现以及如何预防超中