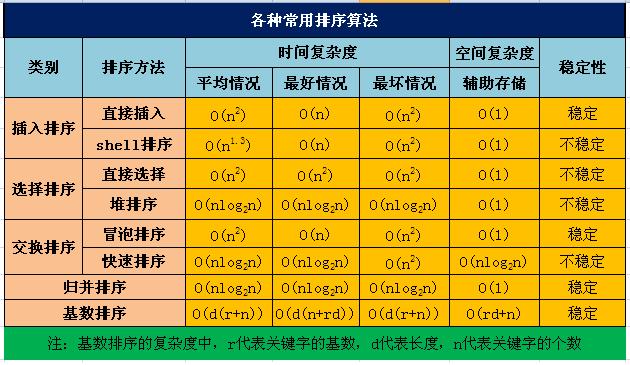
排序算法汇总

Posted 2020-08-13 南飞的孤雁

1. 冒泡排序

1.1 算法原理：

S1：从待排序序列的起始位置开始，从前往后依次比较各个位置和其后一位置的大小并执行S2。
S2：如果当前位置的值大于其后一位置的值，就把他俩的值交换（完成一次全序列比较后，序列最后位置的值即此序列最大值，所以其不需要再参与冒泡）。
S3：将序列的最后位置从待排序序列中移除。若移除后的待排序序列不为空则继续执行S1，否则冒泡结束。

1.2 算法实现（Java）：

1.2.1 基础实现：

public static void bubbleSort(int[] array) {
    int len = array.length;
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j + 1];
                array[j + 1] = array[j];
                array[j] = temp;
            }
        }
    }
}

1.2.2 算法优化：

若某一趟排序中未进行一次交换，则排序结束

public static void bubbleSort(int[] array) {
    int len = array.length;
    boolean flag = true;
    while (flag) {
        flag = false;
        for (int i = 0; i < len - 1; i++) {
            if (array[i] > array[i + 1]) {
                int temp = array[i + 1];
                array[i + 1] = array[j];
                array[i] = temp;
                flag = true;
            }
        }
        len--;
    }
}

2. 快速排序

2.1 算法原理：

快速排序是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此实现整个数据变成有序序列。

2.2 算法实现（Java）：

public static void quickSort(int[] array, int left, int right) {
    if (left < right) {
        int pivot = array[left];
        int low = left;
        int high = right;
        while (low < high) {
            while (low < high && array[high] >= pivot) {
                high--;
            }
            array[low] = array[high];
            while (low < high && array[low] <= pivot) {
                low++;
            }
            array[high] = array[low];
        }
        array[low] = pivot;
        quickSort(array, left, low - 1);
        quickSort(array, low + 1, right);
    }
}

3. 直接插入排序

3.1 算法原理：

插入排序的基本方法是：每步将一个待排序序列按数据大小插到前面已经排序的序列中的适当位置，直到全部数据插入完毕为止。
假设有一组无序序列 $R_0$, $R_1$, … , $R_{n-1}$：
(1) 将这个序列的第一个元素R0视为一个有序序列；
(2) 依次把 $R_1$, $R_2$, … , $R_{n-1}$ 插入到这个有序序列中；
(3) 将$R_i$插入到有序序列中时，前 i-1 个数是有序的，将$R_i$和$R_0$ ~ $R_{i-1}$从后往前进行比较，确定要插入的位置。

3.2 算法实现（Java）：

public static void insertSort(int[] array) {
    for (int i = 1, len = array.length; i < len; i++) {
        if (array[i] < array[i - 1]) {
            int temp = array[i];
            int j;
            for (j = i - 1; j >= 0 && temp < array[j]; j--) {
                array[j + 1] = array[j];
            }
            array[j + 1] = temp;
        }

    }
}

4. Shell排序

4.1 算法原理：

希尔排序是一种插入排序算法，又称作缩小增量排序。是对直接插入排序算法的改进。其基本思想是：
先取一个小于n的整数$h_1$作为第一个增量，把全部数据分成$h_1$个组。所有距离为$h_1$的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量$h_2<h_1$重复上述的分组和排序，直至所取的增量$h_t=1(h_t<h_{t-1}<…<h_2<h_1）$，即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法。

4.2 算法实现（Java）：

public static void shellSort(int[] array) {
    int n = array.length;
    int h;
    for (h = n / 2; h > 0; h /= 2) {
        for (int i = h; i < n; i++) {
            for (int j = i - h; j >= 0; j -= h) {
                if (array[j] > array[j + h]) {
                    int temp = array[j];
                    array[j] = array[j + h];
                    array[j + h] = temp;
                }
            }
        }
    }
}

5. 直接选择排序

5.1 算法原理：

直接选择排序是一种简单的排序方法，它的基本思想是：
第一次从R[0]~R[n-1]中选取最小值，与R[0]交换，
第二次从R[1]~R[n-1]中选取最小值，与R[1]交换，
….，
第i次从R[i-1]~R[n-1]中选取最小值，与R[i-1]交换，
…..，
第n-1次从R[n-2]~R[n-1]中选取最小值，与R[n-2]交换，
共通过n-1次，得到一个从小到大排列的有序序列。

5.2 算法实现（Java）：

public static void selectSort(int[] array) {
    int n = array.length;
    for (int i = 0; i < n; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (array[minIndex] > array[j]) {
                minIndex = j;
            }
        }
        if (i != minIndex) {
            int temp = array[i];
            array[i] = array[minIndex];
            array[minIndex] = temp;
        }
    }
}

6. 堆排序

6.1 算法原理：

6.1.1 二叉堆定义：

二叉堆是完全二叉树或近似完全二叉树。二叉堆满足两个特性：
  1）父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。
  2）每个结点的左子树和右子树都是一个二叉堆。
当父结点的键值总是大于或等于任何一个子节点的键值时为大根堆。当父结点的键值总是小于或等于任何一个子节点的键值时为小根堆。下面展示一个小根堆：

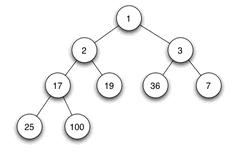
由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

6.1.2 堆的存储：

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

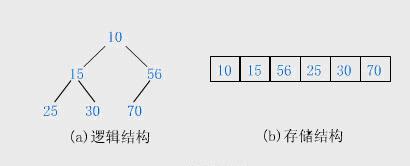
6.1.3 堆的插入：

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，然后将这个新数据插入到这个有序数据中。

6.1.4 堆排序：

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]，小根堆则相反。
堆排序利用了大根堆（或小根堆）堆顶记录的关键字最大（或最小）这一特征，使得在当前无序区中选取最大（或最小）关键字的记录变得简单。
（1）用大根堆排序的基本思想
  ① 先将初始数组$R_1...R_n$建成一个大根堆，此堆为初始的无序区
  ② 再将最大的元素$R_1$（即堆顶）和无序区的最后一个记录$R_n$交换，由此得到新的无序区$R_1...R_{n-1}$和有序区$R_n$，且满足$R_1...R_{n-1}$的值<=$R_n$的值。
  ③由于交换后新的根$R_1$可能违反堆性质，故应将当前无序区$R_1...R_{n-1}$调整为堆。然后再次将$R_1...R_{n-1}$中最大的元素$R_1$和该区间的最后一个记录 排序算法汇总

排序算法汇总

排序算法汇总

内部排序算法汇总

排序算法大汇总

常见排序算法汇总