快速排序系列笔记 quick select

Posted 毛线刷题笔记

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了快速排序系列笔记 quick select相关的知识，希望对你有一定的参考价值。

基础1: partition

 Partition Array

Given an array nums of integers and an int k, partition the array (i.e move the elements in "nums") such that:

  • All elements < k are moved to the left
  • All elements >= k are moved to the right

Return the partitioning index, i.e the first index inums[i] >= k.

Example

If nums = [3,2,2,1] and k=2, a valid answer is 1.

 如果控制条件是 i < j 的话， 那么在如下情况下会出错

[7,7,9,8,6,6,8,7,9,8,6,6], 10

 因为所有数字都小于10，那么i index 应该一直递增到超过j

所以应该为 i <= j

我的代码：

public class Solution {
    /** 
     *@param nums: The integer array you should partition
     *@param k: As description
     *return: The index after partition
     */
    public int partitionArray(int[] nums, int k) {
        //write your code here
        int i = 0, j = nums.length - 1;
        while (i <= j) {
            if (nums[i] < k && nums[j] < k) {
                i++;
            } else if (nums[i] < k && nums[j] >= k) {
                i++;
                j--;
            } else if (nums[i] >= k && nums[j] >= k) {
                j--;
            } else if (nums[i] >= k && nums[j] < k) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                i++;
                j--;
            }
        }
        return i;
    }
}
View Code

其实当左边index的值比k小的时候 i可以一直递增

右边index的值比k大的时候 j可以一直递减

那么当两遍都违背的时候，做一次sawp

简洁到飞起来= = 

public class Solution {
    /** 
     *@param nums: The integer array you should partition
     *@param k: As description
     *return: The index after partition
     */
    public int partitionArray(int[] nums, int k) {
        if(nums == null || nums.length == 0){
            return 0;
        }
        
        int left = 0, right = nums.length - 1;
        while (left <= right) {

            while (left <= right && nums[left] < k) {
                left++;
            }

            while (left <= right && nums[right] >= k) {
                right--;
            }

            if (left <= right) {
                int temp = nums[left];
                nums[left] = nums[right];
                nums[right] = temp;
                
                left++;
                right--;
            }
        }
        return left;
    }
}
partitionArray

----------------------------------------分割线------------------------------- 

Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

For example,
Given [3,2,1,5,6,4] and k = 2, return 5.

这种算法的均摊复杂度是o(n)

T(n) = T(n/2) + o(n)

　　  = T(n/4) + 0(n/2)+o(n)

　　　=...

平均的时间复杂度是o(nlogn), 不理想的情况就是每次partition只排除掉1个点，那么时间复杂度会退化到o(n^2)

 注意几个细节：

1. helper函数是int，递归返回最后的结果，一直返回到最外面一层

2. 这里的partition和前面partition array不同， 以left节点做为pivot，然后从右边开始走，把第一个不符合的放在左边，然后左边开始走，把不符合的放在右边。最后把pivot放回去新的left节点的位置

3. 找第k个大的点 转化为找第length - k + 1的小的点

 public class Solution {
     public int findKthLargest(int[] nums, int k) {
         if (nums == null || nums.length == 0) {
             return -1;
         }
         return helper (nums, nums.length - k + 1, 0, nums.length - 1);
        //length - k + 1 convert the kth large to k\'th small one      
      }
     private int helper(int[] nums, int k, int start, int end) {
         if (start == end) {
             return nums[start];
         }
         
         int pos = partition(nums, start, end);
         if (pos + 1 == k) {
             return nums[pos];
         } else if (pos + 1 > k) {
             return helper (nums, k, start, pos - 1);
         } else {
             /*这个地方为什么是return 下一层递归的结果，因为需要的结果在下层／下下层递归中得到，
　　        把这个值返回来交给最上面的一层*/
             return helper (nums, k,  pos + 1, end);
         }

     }
     
     public int partition(int[] nums, int l, int r) {
        // 初始化左右指针和pivot
        int left = l, right = r;
        int pivot = nums[left];
        
        // 进行partition
        while (left < right) {
            while (left < right && nums[right] >= pivot) {
                right--;
            }
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot) {
                left++;
            }
            nums[right] = nums[left];
        }
        
        // 返还pivot点到数组里面
        nums[left] = pivot;
        return left;         
    }
}
View Code

 

median

这道题是找第k大题目的子集

一样的方法

public class Solution {
    /**
     * @param nums: A list of integers.
     * @return: An integer denotes the middle number of the array.
     */
    public int median(int[] nums) {
        // write your code here
        if (nums == null || nums.length == 0) {
            return -1;
        }
        return helper(nums, 0, nums.length - 1, nums.length / 2 + nums.length %2);
    }
    private int helper(int[] nums, int left, int right, int k) {
        if (left == right) {
            return nums[left];
        }
        int pos = partition(nums, left, right);
        if (pos + 1 == k) {
            return nums[pos];
        } else if (pos + 1 > k) {
            return helper (nums, left, pos - 1, k);
        } else {
            return helper (nums, pos + 1, right, k);
        }
    }
    private int partition (int[] nums, int left, int right) {
        int pivot = nums[left];
        while (left < right) {
            while (left < right && nums[right] >= pivot) {
                right--;
            }
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot) {
                left++;
            }
            nums[right] = nums[left];
        }
        nums[left] = pivot;
        return left;
    }
}
median

-----------------------------分割线-------------------------------------

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

 

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

暴力的方法： 每次取两个array的头一个元素进行比较，谁小谁出列，知道出列了总长度／2. 所以总的时间复杂度为o(k)

把线性时间复杂度再去做优化，只能是logn，如何把线性复杂度优化为logn呢？

涉及到binarysearch的第三层理解，每次做o(1)的操作之后，能保留一半解，也就是说把解的范围缩小一半。

附：binary search 笔记 https://i.cnblogs.com/EditPosts.aspx?postid=5875846

 

利用binary search / quick select的其思想，一次扔掉一半。

代码：

public class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int size1 = nums1.length;
        int size2 = nums2.length;
        int total = size1 + size2;
        if (total % 2 == 0) {
            return 0.5 * (helper(nums1, 0, nums2, 0, (total / 2) ) + helper(nums1, 0, nums2, 0, (total / 2) + 1));
        } else {
            return helper(nums1, 0, nums2, 0, (total / 2) + 1);
        }
    }
    private static int helper (int[] nums1, int start1,
                                int[] nums2, int start2,
                                int k) { //note k denotes the kth number, not the index!!!! eg total == 3 -> k == 2
       // if (start1 == nums1.length){
        if (start1 >= nums1.length){
            return nums2[start2 + k - 1];
        } else if (start2 >= nums2.length) {
            return nums1[start1 + k - 1];
        } else if (k == 1) {
            return Math.min(nums1[start1], nums2[start2]);
        }
        
        int a_key = start1 + k/2  <= nums1.length ? nums1[start1 + k / 2 - 1] : Integer.MAX_VALUE;
        int b_key = start2 + k/2 <= nums2.length ? nums2[start2 + k / 2 - 1] : Integer.MAX_VALUE;
        if (a_key > b_key) {
            return helper (nums1, start1, nums2,start2 + k/2, k - k/2);
        } else {
            return helper (nums1, start1 + k/2, nums2, start2, k - k/2);
        }
    }
}
findMedianSortedArrays

好多好多坑：

1. 通过比较两个数组 a, b的第k/2个数，判断是丢掉a的k/2还是b的k/2。 每次丢掉k／2个数，通过o(1)的操作。总之，随小丢谁

2.两个数组，怎么来丢掉k/2的部分，对于数组来说，其实只要更新一下起始坐标就好了。记住从哪个位置开始是有效的。注意，标记的是起始的坐标，注意index与第xx个的转换。

3. 当a数组非常小，不够k／2个怎么办？

我们不能确保解不在a里面，但是能确保解不在b的k／2里面

那么我们就要扔掉b的前k/2个数，使用了maxValue的小技巧！！

4. 关于奇偶性的问题，总长度为奇数时候，下次层去找k - k/2个，比如 总个数是3， 只能扔掉1个，下一层去找前2个。

5. 递归的出口问题，helper函数里面有3组参数，针对每一组参数都有极限情况

　　a. A没有数了

　　b. b没有数了

　　c. k == 1

　　如果用下面这个判断的话，会出现下面的错误 if (start1 == nums1.length)

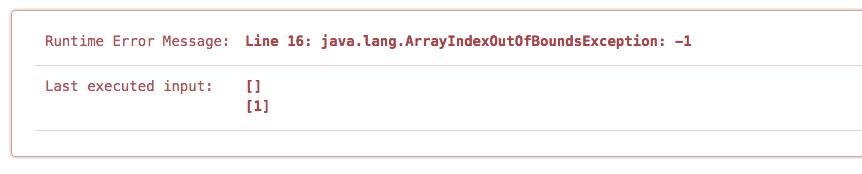
--------------------------分割线-----------------------

 

 

 

 

　　

 

以上是关于快速排序系列笔记 quick select的主要内容，如果未能解决你的问题，请参考以下文章

python 学习笔记 -- 数据结构与算法 快速排序 Quick Sort

排序算法-快速排序（Quick Sort）

快速排序（Quick Sort）及优化

Quick Sort

快速排序 Quick Sort

交换排序—快速排序（Quick Sort）