hdu 5927 Auxiliary Set 贪心
Posted xjhz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了hdu 5927 Auxiliary Set 贪心相关的知识,希望对你有一定的参考价值。
Auxiliary Set
Time Limit: 9000/4500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Problem Description
Given a rooted tree with n vertices, some of the vertices are important.
An auxiliary set is a set containing vertices satisfying at least one of the two conditions:
?It is an important vertex
?It is the least common ancestor of two different important vertices.
You are given a tree with n vertices (1 is the root) and q queries.
Each query is a set of nodes which indicates the unimportant vertices in the tree. Answer the size (i.e. number of vertices) of the auxiliary set for each query.
An auxiliary set is a set containing vertices satisfying at least one of the two conditions:
?It is an important vertex
?It is the least common ancestor of two different important vertices.
You are given a tree with n vertices (1 is the root) and q queries.
Each query is a set of nodes which indicates the unimportant vertices in the tree. Answer the size (i.e. number of vertices) of the auxiliary set for each query.
Input
The first line contains only one integer T (T), which indicates the number of test cases.
For each test case, the first line contains two integers n (1≤n≤100000), q (0≤q).
In the following n -1 lines, the i-th line contains two integers ui,vi(1≤ui,vi≤n) indicating there is an edge between uii and vi in the tree.
In the next q lines, the i-th line first comes with an integer mi(1≤mi≤100000) indicating the number of vertices in the query set.Then comes with mi different integers, indicating the nodes in the query set.
It is guaranteed that ∑q.
It is also guaranteed that the number of test cases in which n≥1000 or ∑q is no more than 10.
For each test case, the first line contains two integers n (1≤n≤100000), q (0≤q).
In the following n -1 lines, the i-th line contains two integers ui,vi(1≤ui,vi≤n) indicating there is an edge between uii and vi in the tree.
In the next q lines, the i-th line first comes with an integer mi(1≤mi≤100000) indicating the number of vertices in the query set.Then comes with mi different integers, indicating the nodes in the query set.
It is guaranteed that ∑q.
It is also guaranteed that the number of test cases in which n≥1000 or ∑q is no more than 10.
Output
For each test case, first output one line "Case #x:", where x is the case number (starting from 1).
Then q lines follow, i-th line contains an integer indicating the size of the auxiliary set for each query.
Then q lines follow, i-th line contains an integer indicating the size of the auxiliary set for each query.
Sample Input
1
6 3
6 4
2 5
5 4
1 5
5 3
3 1 2 3
1 5
3 3 1 4
Sample Output
Case #1:
3
6
3
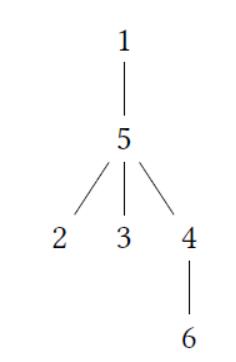 For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
Hint
 For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
Source
思路:记录儿子个数,子树的全删掉就是删掉一儿子;
#include<bits/stdc++.h> using namespace std; #define ll long long #define pi (4*atan(1.0)) #define eps 1e-14 const int N=2e5+10,M=4e6+10,inf=1e9+10,mod=1e9+7; const ll INF=1e18+10; vector<int>v[N]; int si[N],fa[N],deep[N],a[N],change[N]; int n,m,q; void init() { for(int i=0;i<=n;i++) { change[i]=0; fa[i]=0; si[i]=0; deep[i]=0; v[i].clear(); } } void dfs(int u,int pre,int dep) { deep[u]=dep; for(int i=0;i<v[u].size();i++) { if(v[u][i]==pre)continue; si[u]++;dfs(v[u][i],u,dep+1); fa[v[u][i]]=u; } } int cmp(int a,int b) { return deep[a]>deep[b]; } int main() { int T,cas=1; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&q); init(); for(int i=1;i<n;i++) { int u,w; scanf("%d%d",&u,&w); v[u].push_back(w); v[w].push_back(u); } dfs(1,0,1); printf("Case #%d:\n",cas++); while(q--) { int ans=0; scanf("%d",&m); for(int i=1;i<=m;i++) scanf("%d",&a[i]); sort(a+1,a+1+m,cmp); for(int i=1;i<=m;i++) { int FA=fa[a[i]]; if(si[a[i]]==0) { si[FA]--; change[FA]++; } if(si[a[i]]>=2) { ans++; } } printf("%d\n",n-m+ans); for(int i=1;i<=m;i++) { int FA=fa[a[i]]; if(change[FA]) { si[FA]+=change[FA]; change[FA]=0; } } } } return 0; }
以上是关于hdu 5927 Auxiliary Set 贪心的主要内容,如果未能解决你的问题,请参考以下文章