分类模型评估

Posted 2020-08-13 dataAlpha

一直对于各种分类器评估的指标有点晕，今天决定琢磨下，并且写下来，方便以后回忆。

一、混淆矩阵

 

来源于信息论，根据上面的混淆矩阵，有3个指标需要搞清楚，我觉得记公式真的很容易搞混，建议大家都直接记文字加上自己理解就好了。

准确率=正确预测正负的个数/总个数（这个指标在python中的交叉验证时可以求准确率）

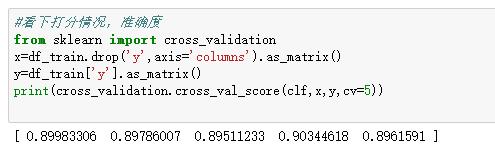
覆盖率（也叫作召回率）=正确预测正的个数/实际正的个数 （当然也可以是负覆盖率）

命中率=正确预测正的个数/预测正的个数

以上指标，在Python中提供混淆矩阵的报告

二、ROC

之所以又有ROC曲线，是因为，前面的准确率和召回率存在缺陷。从准确率来说，如果我们关心的是y=1，而恰好y=1的样本个数又很少，此时用准确率的指标就可能不靠谱了，有个比较好的例子如下：测试样本中有A类样本90个，B 类样本10个。分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。则C1的分类精度为 90%，C2的分类精度为75%。但是，显然C2更有用些，因为它分对了我们更关心的B类。

召回率TPR(True Positive Rate) =TP/(TP+FN) ＝ a / (a+b)

取伪率FPR(False Positive Rate) = FP/(FP+TN) = c / (c+d)

ROC空间将取伪率（FPR）定义为 X 轴，召回率（TPR）定义为 Y 轴。

召回率和取伪率是会同时提高和降低的，也就是召回率越高，取伪率肯定也就越高了，比如极端的情况下，我们把左右的样本都认为y=1那召回率肯定是等于1，而取伪率肯定也会变成1了。

ROC是怎么画出来的呢，例如在一个二分类模型中，对于所预测得到概率结果，假设已确定一个阈值，比如说 0.6，大于这个值的实例划归为正类，小于这个值则划到负类中。如果减小阈值，减到0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例的比例，即TPR，但同时也将更多的负实例当作了正实例，即提高了FPR。为了形象化这一变化，在此引入ROC。

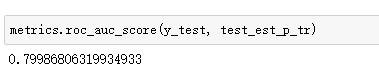
虽然，用ROC curve来表示分类器的performance很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。于是AUC就出现了，其值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的模型表现。

三、提升度

• 正例的比例Pi1 ＝ (a+b) / (a+b+c+d) ；
• 预测成正例的比例 Depth ＝  (a+c) / (a+b+c+d) ；
• 正确预测到的正例数占预测正例总数的比例 PV_plus ＝ a / (a+c) ；
• 提升值 Lift ＝ (a / (a+c) ) / ((a+b) / (a+b+c+d)) = PV_plus / Pi1

Lift衡量的是，与不利用模型相比，模型的预测能力“变好”了多少。不利用模型，我们只能利用“正例的比例是 (a+b) / (a+b+c+d) ”这个样本信息来估计正例的比例（baseline model），而利用模型之后，我们不需要从整个样本中来挑选正例，只需要从我们预测为正例的那个样本的子集（a+c）中挑选正例，这时预测的准确率为a / (a+c)。

显然，lift(提升指数)越大，模型的运行效果越好。如果a / (a+c)就等于(a+b) / (a+b+c+d)（lift等于1），这个模型就没有任何“提升”了（套一句金融市场的话，它的业绩没有跑过市场）。