Tree Restoring

Posted 2020-08-12 mxzf0213

Tree Restoring

---

Time limit : 2sec / Memory limit : 256MB

Score : 700 points

Problem Statement

Aoki loves numerical sequences and trees.

One day, Takahashi gave him an integer sequence of length N, a1,a2,…,aN, which made him want to construct a tree.

Aoki wants to construct a tree with N vertices numbered 1 through N, such that for each i=1,2,…,N, the distance between vertex i and the farthest vertex from it is ai, assuming that the length of each edge is 1.

Determine whether such a tree exists.

Constraints

• 2≦N≦100
• 1≦ai≦N−1

---

Input

The input is given from Standard Input in the following format:

N
a1 a2 … aN

Output

If there exists a tree that satisfies the condition, print Possible. Otherwise, print Impossible.

---

Sample Input 1

5
3 2 2 3 3

Sample Output 1

Possible

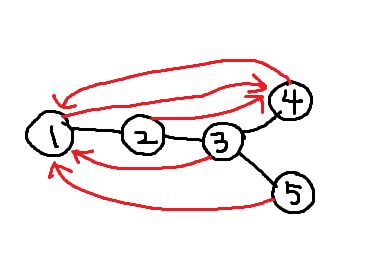
The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.

分析：对于一棵树来说，假设直径有两个端点a，b，那么任意一点到其他点最远距离必然是max(dist(p,a),dist(p,b))，

　　　那么根据直径来构树，以树直径为奇数举例，那么这条链上必然有偶数个点，且最远距离为k,k-1,...,k/2,k/2...,k-1,k；

　　　那么也就是不存在最远距小于k/2的点，且k/2有两个点，大于k/2的至少有2个；

　　　树直径为偶数时同理；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=1e5+10;
using namespace std;
ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p;p=p*p;q>>=1;}return f;}
int n,m,k,t;
inline ll read()
{
    ll x=0;int f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
    return x*f;
}
int a[maxn],ma,vis[maxn];
bool flag;
int main()
{
    int i,j;
    scanf("%d",&n);
    rep(i,1,n)scanf("%d",&a[i]),vis[a[i]]++,ma=max(ma,a[i]);
    if(ma%2==0)
    {
        rep(i,1,ma/2-1)if(vis[i])flag=true;
        rep(i,ma/2,ma)
        {
            if(i==ma/2)
            {
                if(vis[i]!=1)flag=true;
            }
            else if(vis[i]<2)flag=true;
        }
    }
    else
    {
        rep(i,1,(ma+1)/2-1)if(vis[i])flag=true;
        rep(i,(ma+1)/2,ma)
        {
            if(i<(ma+1)/2&&vis[i])flag=true;
            if(i==(ma+1)/2)
            {
                if(vis[i]!=2)flag=true;
            }
            else if(vis[i]<2)flag=true;
        }
    }
    if(flag)puts("Impossible");
    else puts("Possible");
    //system("Pause");
    return 0;
}