第三次作业

Posted 2020-08-10

2.利用程序huff_enc和huff_dec进行以下操作（在每种情下，利用由被压缩生成的码本）。

(a)对Sena、Sensin和Omaha图像进行编码。

解：用表格的形式给出对应文件压缩前后的大小为（单位用字节表示）

图像名称	压缩前	压缩后	压缩率
Sena	64k（65536Byte）	57k（58368Byte）	89%
Sensin	64k（65536Byte）	61K（62464Byte）	95%
Omaha	64k（65536Byte）	57K（58368Byte）	91%

 

4.一个信源从符号集A={a1，a2,a3,a4,a5}中选择字母，概率为P（a1）=0.15,P（a2）=0.04,P（a3）=0.26,P（a4）=0.05,P（a1）=0.50.

(a)计算这个信源的熵。

(b)求这个信源的霍夫曼码。

(c)求（b）中代码的平均长度及其冗余度。

答：

(a)H=-[p(a1)*log2p(a1)+p(a2)*log2p(a2)+p(a3)*log2p(a3)+p(a4)*log2p(a4)+p(a5)*log2p(5)]

  =-(0.15*log20.15+0.04*log20.04+0.26*log20.26+0.05*log20.05+0.50*log20.50)

=0.4105+0.1858+0.5053+0.2161+0.5

=1.8177 bits/symbol

(b) 这个信源的霍夫曼码为：

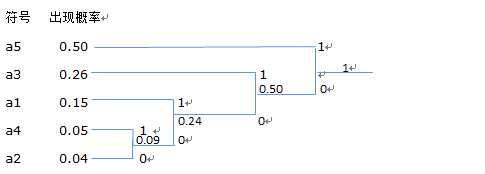
a1的编码为：001

a2的编码为：0000

a3的编码为：01

a4的编码为：0001

a5的编码为：1 

 

(c)平均长度

l=p(a1)*l(a1)+p(a2)*l(a2)+p(a3)*l(a3)+p(a4)*l(a4)+p(a5)*l(a5)

          =0.15*3+0.04*4+0.26*2+0.05*4+0.50*1

=1.83bit

冗余度r=Hmax(x)-H(X)=logm=H(X)=1.83-0.8177=1.0123

 

2、 思考：为什么压缩领域中的编码方法总和二叉树联系在一起呢？

答：因为为了使用不固定的码长表示单个字符，编码必须符合前缀编码的要求，即较短的编码决不能是较长编码的前缀。要构造符合这一要求的二进制编码体系，二叉树是最理想的选择。

举例如下：

        

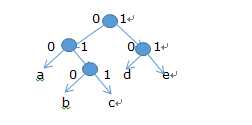
要编码的字符总是出现在树叶上，假定从根向树叶行走的过程中，左转为0，右转为 

1，则一个字符的编码就是从根走到该字符所在树叶的路径。正因为字符只能出现在 

树叶上，任何一个字符的路径都不会是另一字符路径的前缀路径，所以得出符合要求的前缀 

编码为： 

a ： 00

b ： 010 

c ：011 

d ：10 

e ：11