HDU - 3966 Aragorn's Story（树链剖分入门+线段树）

Posted 2020-08-09 酱油党gsh

HDU - 3966 Aragorn‘s Story Time Limit: 3000MS   Memory Limit: 32768KB   64bit IO Format: %I64d & %I64u Submit Status Description Our protagonist is the handsome human prince Aragorn comes from The Lord of the Rings. One day Aragorn finds a lot of enemies who want to invade his kingdom. As Aragorn knows, the enemy has N camps out of his kingdom and M edges connect them. It is guaranteed that for any two camps, there is one and only one path connect them. At first Aragorn know the number of enemies in every camp. But the enemy is cunning , they will increase or decrease the number of soldiers in camps. Every time the enemy change the number of soldiers, they will set two camps C1 and C2. Then, for C1, C2 and all camps on the path from C1 to C2, they will increase or decrease K soldiers to these camps. Now Aragorn wants to know the number of soldiers in some particular camps real-time. Input Multiple test cases, process to the end of input.  For each case, The first line contains three integers N, M, P which means there will be N(1 ≤ N ≤ 50000) camps, M(M = N-1) edges and P(1 ≤ P ≤ 100000) operations. The number of camps starts from 1.  The next line contains N integers A1, A2, ...AN(0 ≤ Ai ≤ 1000), means at first in camp-i has Ai enemies.  The next M lines contains two integers u and v for each, denotes that there is an edge connects camp-u and camp-v.  The next P lines will start with a capital letter ‘I‘, ‘D‘ or ‘Q‘ for each line.  ‘I‘, followed by three integers C1, C2 and K( 0≤K≤1000), which means for camp C1, C2 and all camps on the path from C1 to C2, increase K soldiers to these camps.  ‘D‘, followed by three integers C1, C2 and K( 0≤K≤1000), which means for camp C1, C2 and all camps on the path from C1 to C2, decrease K soldiers to these camps.  ‘Q‘, followed by one integer C, which is a query and means Aragorn wants to know the number of enemies in camp C at that time. Output For each query, you need to output the actually number of enemies in the specified camp. Sample Input 3 2 5 1 2 3 2 1 2 3 I 1 3 5 Q 2 D 1 2 2 Q 1 Q 3 Sample Output 7 4 8 Hint   1.The number of enemies may be negative. 2.Huge input, be careful. Source 2011 Multi-University Training Contest 13 - Host by HIT     题解：题目大意是给你一棵树，树有对应的点权，然后给你q个命令，可以进行对某条链上的所有点值进行加减，或者对某个点的权值进行查询。 这是一道典型的树链剖分问题。所谓树链剖分就是将树上的点按链的方式连续标号，类似离散化，这样我们就可以利用这个特性，讲问题改变为区间问题，就可以套用线段树或者树状数组去解决这一类问题。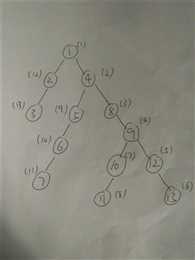 如上图，经过树链剖分算法后，每个点离散后的id值为括号上的值。跑完树链剖分后，我们把树分成了四条链，分别为1-4-8-9-12-13，2-3，5-6-7，10-11，注意到链上的点都是连续的，当我们要进行区间操作时，可以套个线段树。 那树链剖分又是怎么进行的呢？首先要把树分成几条链，分链前先介绍一个概念——重儿子。我们先定义一个数组size保存当前结点的所有子树上的点的个数，如上图size[3]=1,size[2]=2,size[9]=5...而一个结点的重儿子就是该结点的儿子中size的值最大的那个，比如1的重儿子是4，4的重儿子是8。知道重儿子后，就可以分链了。我们只要遍历每一个结点，把每个结点和他的重儿子连接起来，这样就把链分开了，但因为我们要对他进行顺序标号，所以可以利用dfs标号 代码如下：（可以按照上图模拟一下，模拟几次就懂了） #include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <vector> #include <queue> #include <stack> #include <map> #include <set> #define X first #define Y second #define clr(u,v); memset(u,v,sizeof(u)); #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #pragma comment(linker, "/STACK:1024000000,1024000000") using namespace std; typedef pair<int,int> pii; const int maxn=50010; const int INF=0x3f3f3f3f; struct Edge { int v,to; }E[maxn*2]; int n,m,q; int head[maxn],cnt; int cost[maxn]; int size[maxn],deep[maxn],F[maxn],son[maxn],tot,top[maxn],id[maxn]; int add[maxn<<2],sum[maxn<<2]; void init() { clr(head,-1); cnt = 0; clr(size,0); clr(son,0); clr(sum,0); clr(add,0); tot = 1; } void addedge(int v,int u) { E[cnt].v=u,E[cnt].to=head[v]; head[v]=cnt++; } //以下为树链剖分部分 void dfs1(int cur ,int pre,int d) { deep[cur] = d;//记录深度 size[cur] = 1;//记录子树的所有结点数 F[cur] = pre;//记录该结点的父亲结点 for (int i=head[cur];~i;i=E[i].to) { int v=E[i].v; if (v == pre) continue ; dfs1(v,cur,d+1); size[cur]+=size[v];//回溯更新size值 } if (size[son[pre]]<size[cur]) son[pre]=cur;//更新重儿子 } void dfs2(int cur,int fa)//第一个参数代表当前结点，第二个参数代表该链上的祖先结点 { top[cur] = fa;//top记录该点所在链上的祖先结点 id[cur] = tot++;//对每个结点进行标号 if (son[cur]) dfs2(son[cur],fa);//如果该结点有重儿子，继续深搜下去，由于还是那条链，所以还是传fa for (int i=head[cur];~i;i=E[i].to)//遍历其他儿子结点 { int v=E[i].v; if (son[cur]!=v&&F[cur]!=v) dfs2(v,v);//由于该儿子结点不在当前结点的链上，所以要新开一条链，该链的祖先结点设置为自己 } } //以下为线段树部分 void PushUp(int rt) { sum[rt]=max(sum[rt<<1],sum[rt<<1|1]); } void PushDown(int rt,int m) { if (add[rt]) { add[rt<<1]+=add[rt]; add[rt<<1|1]+=add[rt]; sum[rt<<1]+=add[rt]*(m-(m>>1)); sum[rt<<1|1]+=add[rt]*(m>>1); add[rt]=0; } } void update(int L,int R,int c,int l,int r,int rt) { if (L<=l&&r<=R) { add[rt]+=c; sum[rt]+=c*(r-l+1); return ; } PushDown(rt,r-l+1); int m=(l+r)>>1; if (L<=m) update(L,R,c,lson); if (R>m) update(L,R,c,rson); PushUp(rt); } int query(int L,int R,int l,int r,int rt) { if (L<=l&&r<=R) return sum[rt]; PushDown(rt,r-l+1); int m=(l+r)>>1; int ret=0; if (L<=m) ret+=query(L,R,lson); if (m<R) ret+=query(L,R,rson); return ret; } //以下为修改部分 void change(int x,int y,int val) { while (top[x]!=top[y])//判断两个结点是不是在同一条链上，如果不是，则进行下列操作 { if (deep[top[x]]<deep[top[y]]) swap(x,y);//找一个深度深的点 update(id[top[x]],id[x],val,1,n,1);//更新改点到其链上祖先的点上的所有值 x=F[top[x]];//并把该点更新为该链上祖先结点的父亲结点 } if (deep[x]>deep[y]) swap(x,y);//此时两个结点在同一条链上 update(id[x],id[y],val,1,n,1);//直接更新x~y上的所有点 } int main() { #ifdef LOCAL freopen("data","r",stdin); #endif while (~scanf("%d%d%d",&n,&m,&q)) { init(); for (int i=1;i<=n;i++) scanf("%d",&cost[i]); int u,v; while (m--) { scanf("%d%d",&v,&u); addedge(v,u); addedge(u,v); } int root = 1; dfs1(root,0,0); dfs2(root,root); for (int i=1;i<=n;i++) update(id[i],id[i],cost[i],1,n,1); char str[5]; int a,b,c; while (q--) { scanf("%s",str); if (str[0] == ‘I‘) { scanf("%d%d%d",&a,&b,&c); change(a,b,c); } else if (str[0] == ‘Q‘) { scanf("%d",&a); int ans = query(id[a],id[a],1,n,1); printf("%d\n",ans); } else { scanf("%d%d%d",&a,&b,&c); change(a,b,-c); } } } return 0; }