Caffe中Solver方法(HGL)
Posted LeonHuo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Caffe中Solver方法(HGL)相关的知识,希望对你有一定的参考价值。
线性回归:是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
对于一般训练集:
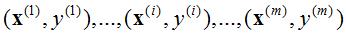
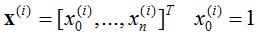
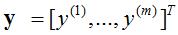
参数系统为:
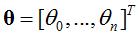
线性模型为:
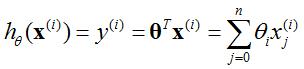
损失函数最小的目标就是求解全局最小值,loss函数定义为
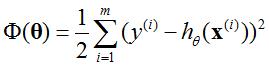
目标:min Φ(θ),loss函数最小。估计最优系数(θ0, θ1, θ2, …, θn)。
1. 梯度下降法(最速下降法)
顾名思义,梯度下降法的计算过程就是沿梯度下降的方向求解极小值。
具体过程如下(如图1所示):
- 首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量(初值的选择非常影响梯度下降算法的好与坏)。
- 改变θ的值,使得Φ(θ)按梯度下降的方向进行减少。
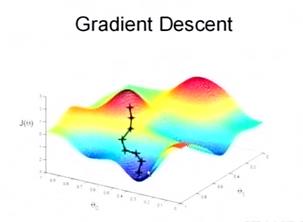
图1 梯度下降描述(来自于斯坦福大学,《机器学习》公开课[2])
过程2)可以表示为:
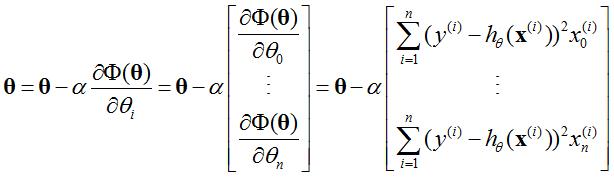
其中α为步长。
由于我们每进行一次参数更新需要计算整体训练数据的梯度,批量梯度下降会变得很慢,并且会遇到内存吃不下数据就挂了。同时批量梯度下降也无法支持模型的在线更新,例如,新的样本不停的到来。
2. SGD (随机梯度下降算法,Stochastic gradient descent)
在梯度下降中,对于θ的更新,所有的样本都有贡献,也就是参与调整θ,其计算得到的是一个标准梯度。如果数据量非常大,那么运算速度很慢。而随机梯度下降算法的随机也就是说我用样本中的一个例子来近似我所有的样本,来调整θ。这样速度更快,但是更容易陷入局部极小。随机梯度下降算法可以表示为:
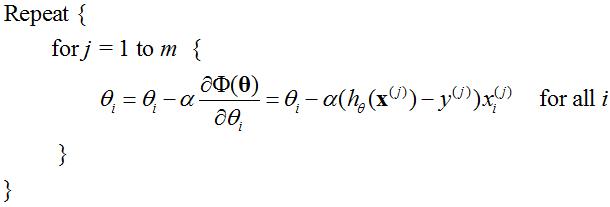
每次只选用第i个样本,m为样本数量。
3. AdaGrad(自适应梯度,Adaptive Gradient)
自适应梯度与SGD类似,AdaGrad的更新速率是可变的。更新速率一定,不一定适合所有的更新阶段。所以AdaGrad调整的是Gradient,对于所有的参数,随着更新的总距离增多,学习速度随之变缓。可以表示为:
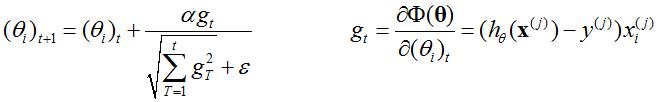
其中(θi)t是t步的参数,ε很小,保证非0。
缺点:学习率单调递减,训练后期学习率非常小;需要手动设置全局学习率;更新 θt时,左右两边单位不统一。
参考文献:Duchi, E. Hazan, and Y. Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
4. AdaDelta
AdaDelta基本思想是用一阶的方法,近似模拟二阶牛顿法,是对AdaGrad的缺点进行改进。可表示为:
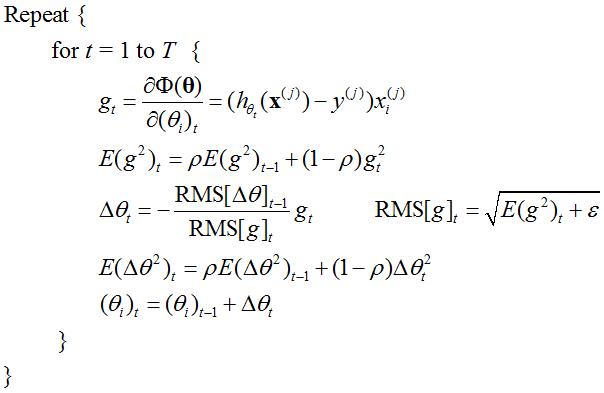 ?
?
5. RMSprop
RMSprop和Adadelta是在差不多的时间各自独立产生的工作,目的都是为了缓解Adagrad的学习速率减少的问题。实际上RMSprop和我们在Adadelta中推到的第一个更新向量是相同的:
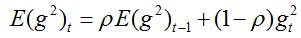
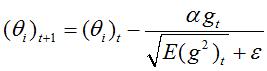
其中,ρ建议取0.9,α建议取0.001。
6. NAG
这个算法严格的说来是凸优化中的算法,具有O(1/t^2)的收敛率,收敛速度比较快。因为 DNN是一个non-convex的model,所以NAG方法并不能达到这个收敛速度。caffe文档中指出,这个方法对于某些deeplearning 的 architecture是非常有效的。与SGD类似,具体更新过程如下:
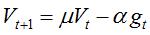
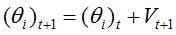
7. Adam(个人认为一般都合适的caffe的solver方法)
Adaptive Moment Estimation(Adam) 也是一种不同参数自适应不同学习速率方法,与Adadelta与RMSprop区别在于,它计算历史梯度衰减方式不同,不使用历史平方衰减,其衰减方式类似动量,如下[4]:
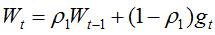
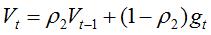
Wt与Vt分别是梯度的带权平均和带权有偏方差,初始为0向量,Adam的作者发现他们倾向于0向量(接近于0向量),特别是在衰减因子(衰减率)ρ1,ρ2接近于1时。为了改进这个问题,对Wt与Vt进行偏差修正(bias-corrected):
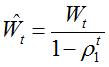
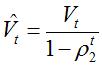
最终,Adam的更新方程为:
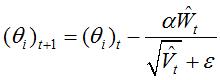
[1] http://www.cnblogs.com/denny402/
[2] http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html
[3] http://blog.sina.com.cn/s/blog_eb3aea990102v41r.html
[4] http://blog.csdn.net/heyongluoyao8/article/details/52478715?locationNum=7
以上是关于Caffe中Solver方法(HGL)的主要内容,如果未能解决你的问题,请参考以下文章