Splay Tree(伸展树)
Posted __AiR_H
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Splay Tree(伸展树)相关的知识,希望对你有一定的参考价值。
参考:《数据结构(C++语言版)》邓俊辉著 (好书
一、
伸展树(由 D. D. Sleator 和 R. E. Tarjan 于 1985 年发明)也是平衡二叉搜索树的一种形式。相对于 AVL 树,伸展树的实现更为简洁
伸展树无需时刻都严格地保持全树的平衡,但却能够在任何足够长的真实操作序列中,保持分摊意义上的高效率
伸展树也不需要对基本的二叉树节点结构做任何附加的要求或改动,更不需要记录平衡因子或高度之类的额外信息,故适用范围更广
二、局部性
信息处理的典型模式是,将所有的数据项视作一个集合,并将其组织为某种适宜的数据结构,进而借助操作接口高效访问
为考查和评价各操作接口的效率,除了从最坏情况的角度出发,也可假定所有操作彼此独立、次序随机且概率相等,并从平均情况的角度出发
然而,后一尺度所依赖的假定条件, 往往并不足以反映真实的情况
实际上, 通常在任意数据结构的生命期内, 不仅执行不同操作的概率往往极不均衡,而且各操作之间具有极强的相关性, 并在整体上多呈现出极强的规律性
其中最为典型的,就是所谓的“数据局部性”( data locality) ,这包括两个方面的含义:
- 刚刚被访问过的元素, 极有可能在不久之后再次被访问到
- 将被访问的下一元素, 极有可能就处于不久之前被访问过的某个元素的附近
充分利用好此类特性,即可进一步地提高数据结构和算法的效率
就二叉搜索树而言,数据局部性具体表现为:
- 刚刚被访问过的节点, 极有可能在不久之后再次被访问到
- 将被访问的下一节点, 极有可能就处于不久之前被访问过的某个节点的附近
因此, 只需将刚被访问的节点,及时地“转移”至树根( 附近) , 即可加速后续的操作
当然,转移前后的搜索树必须相互等价
三、逐层伸展
1、简易伸展树
一种直接方式是:每访问一个节点之后,随即反复地以它的父节点为轴,经适当的旋转将其提升一层,直至最终成为树根
以图 1 为例,若深度为 3 的节点 E 刚被访问 -- 无论查找或插入,甚至“删除” -- 都可通过 3 次旋转,将该树等价变换为以 E 为根的另一棵二叉搜索树
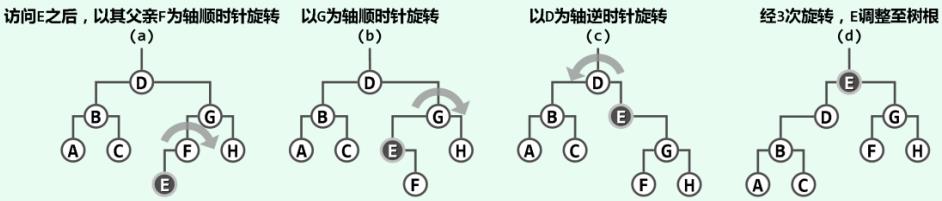
图 1 通过自下而上的一系列等价变换,可使任一节点上升至树根
随着节点 E 的逐层上升,两侧子树的结构也不断地调整,故这一过程也称作伸展(splaying)
而采用这一调整策略的二叉搜索树也因此得名
不过,为实现真正意义上的伸展树,还须对以上策略做点微秒而本质的改进
之所以改进,是因为目前的策略仍存在致命的缺陷 -- 对于很多访问序列,单次访问的分摊时间复杂度在极端情况下可能高达 Ω(n)
2、最坏情况
不难验证,若从空树开始依次插入关键码 {1,2,3,4,5},且其间采用如上调整策略,则可得到如图 2 所示的二叉搜索树
接下来,若通过 search() 接口,再由小到大地依次访问各节点一次,则该树在各次访问之后的结构形态将如图(b ~ f)所示

图 2 简易伸展树的最坏情况
可见,在各次访问之后, 为将对应节点伸展调整至树根,分别需做 4、 4、 3、 2 和 1 次旋转
一般地,若节点总数为 n,则旋转操作的总次数应为:
(n - 1) + { (n - 1) + (n - 2) + ... + 1 } = (n^2 + n - 2) / 2 = Ω(n^2)
如此分摊下来,每次访问平均需要 Ω(n) 时间
很遗憾,这一效率不仅远远低于 AVL 树, 而且甚至与原始的二叉搜索树的最坏情况相当
而事实上,问题还远不止于此
稍做比对即不难发现, 图 2(a) 与 (f) 中二叉搜索树的结构完全相同
也就是说,经过以上连续的 5 次访问之后, 全树的结构将会复原!这就意味着,以上情况可以持续地再现
当然, 这一实例, 完全可以推广至规模任意的二叉搜索树
于是对于规模为任意 n 的伸展树,只要按关键码单调的次序, 周期性地反复进行查找
则无论总的访问次数 m >> n 有多大, 就分摊意义而言, 每次访问都将需要 Ω(n) 时间!
那么,这类最坏的访问序列能否回避?具体地,又应该如何回避?
四、双层伸展
为克服上述伸展调整策略的缺陷,一种简便且有效的方法就是:将逐层伸展改为双层伸展
具体地,每次都从当前节点v向上追溯两层(而不是仅一层) , 并根据其父亲p以及祖父g的相对位置, 进行相应的旋转
以下分三类情况, 分别介绍具体的处理方法
1、zig-zig / zag-zag
如图 3(a) 所示,设 v 是 p 的左孩子,且 p 也是 g 的左孩子
设 W 和 X 分别是 v 的左、右子树, Y 和 Z 分别是 p 和 g 的右子树

图 3 通过 zig-zig 操作,将节点v上推两层
针对这种情况,首先以节点 g 为轴做顺时针旋转 zig(g), 其效果如图 (b) 所示
然后,再以 p 为轴做顺时针旋转 zig(p), 其效果如图 (c) 所示
如此连续的两次 zig 旋转, 合称 zig-zig 调整
自然地, 另一完全对称的情形 -- v 是 p 的右孩子,且 p 也是 g 的右孩子 -- 则可通过连续的两次逆时针旋转实现调整, 合称 zag-zag 操作
2、zig-zag / zag-zig
如图 4(a) 所示,设 v 是 p 的左孩子,而 p 是 g 的右孩子
设 W 是 g 的左子树, X 和 Y 分别是 v 的左、右子树, Z 是 p 的右子树
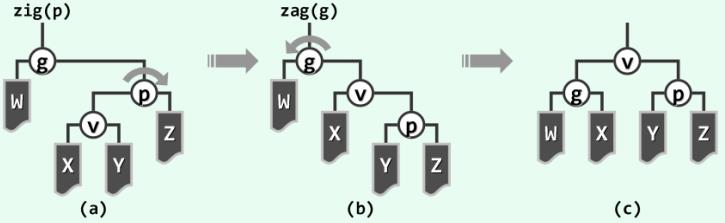
图 4 通过 zig-zag 操作,将节点 v 上推两层
针对这种情况,首先以节点 p 为轴做顺时针旋转 zig(p), 其效果如 (b) 所示
然后,再以 g 为轴做逆时针旋转 zag(g), 其效果如图 (c) 所示
如此 zig 旋转再加 zag 旋转, 合称 zig-zag 调整
同样地, 另一完全对称的情形 -- v 是 p 的右孩子,而 p 是 g 的左孩子 -- 则可通过 zag 旋转再加 zig 旋转实现调整, 合称 zag-zig 操作
3、zig / zag
如图 5(a) 所示,若 v 最初的深度为奇数,则经过若干次双层调整至最后一次调整时, v 的父亲 p 即是树根 r
将 v 的左、右子树记作 X 和 Y,节点 p = r 的另一子树记作 Z
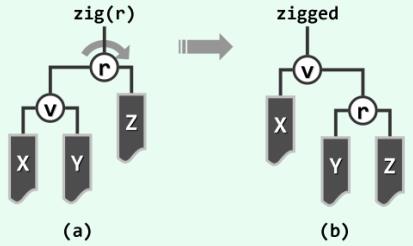
图 5 通过 zig 操作,将节点 v 上推一层,成为树根
此时,只需围绕 p = r 做顺时针旋转 zig(p),即可如图 (b) 所示, 使 v 最终攀升至树根,从而结束整个伸展调整的过程
zag 调整与之对称
4、效果与效率
综合以上各种情况,每经过一次双层调整操作,节点 v 都会上升两层
若v的初始深度 depth(v) 为偶数,则最终 v 将上升至树根
若 depth(v) 为奇数,则当 v 上升至深度为 1 时,不妨最后再相应地做一次 zig 或 zag 单旋操作
无论如何,经过 depth(v) 次旋转后, v 最终总能成为树根
重新审视图 2 的最坏实例不难发现,这一访问序列导致 Ω(n) 平均单次访问时间的原因,可以解释为:
在这一可持续重复的过程中,二叉搜索树的高度始终不小于 n/2
而且,至少有一半的节点在接受访问时,不仅没有如最初设想的那样靠近树根, 而且反过来恰恰处于最底层
从树高的角度看,问题根源也可再进一步地解释为:
在持续访问的过程中, 树高依算术级数逐步从 n - 1 递减至 n/2 ,然后再逐步递增回到 n - 1
那么, 采用上述双层伸展的策略将每一刚被访问过的节点推至树根, 可否避免如图 2 所示的最坏情况呢?
稍作对比不难看出,就调整之后的局部结构而言, zig-zag 和 zag-zig 调整与此前的逐层伸展完全一致( 亦等效于 AVL 树的双旋调整),而 zig-zig 和 zag-zag 调整则有所不同
事实上,后者才是双层伸展策略优于逐层伸展策略的关键所在
以如图 6(b) 所示的二叉搜索树为例,在 find(1) 操作之后采用逐层调整策略与双层调整策略的效果, 分别如图 (a) 和图 (c) 所示
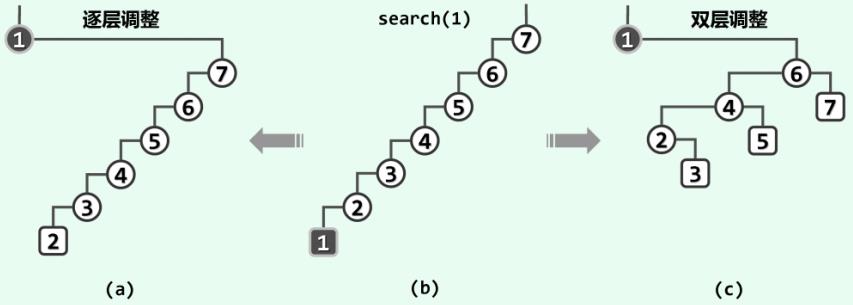
图 6 双层调整策略的高度折半效果
可见,最深节点( 1)被访问之后再经过双层调整, 不仅同样可将该节点伸展至树根,而且同时可使树的高度接近于减半
就树的形态而言,双层伸展策略可“ 智能” 地“折叠” 被访问的子树分支,从而有效地避免对长分支的连续访问
这就意味着, 即便节点 v 的深度为 Ω(n),双层伸展策略既可将 v 推至树根, 亦可令对应分支的长度以几何级数( 大致折半)的速度收缩
图 7 则给出了一个节点更多、更具一般性的例子,从中可更加清晰地看出这一效果
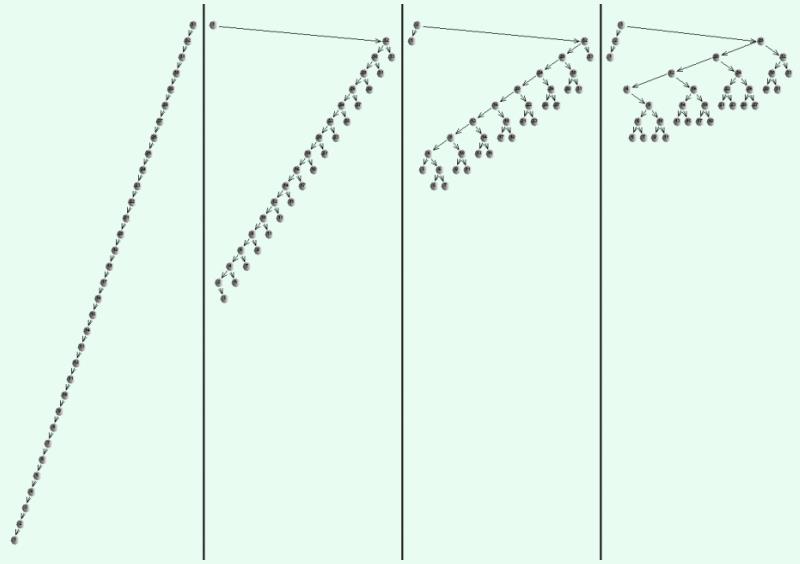
图 7 伸展树中较深的节点一旦被访问到,对应分支的长度将随即减半
尽管在任一时刻伸展树中都可能存在很深的节点,但与含羞草类似地, 一旦这类“ 坏” 节点被“碰触” 到, 经过随后的双层伸展, 其对应的分支都会收缩至长度大致折半
于是, 即便每次都“ 恶意地” 试图访问最底层节点,最坏情况也不会持续发生
可见,伸展树虽不能杜绝最坏情况的发生, 却能有效地控制最坏情况发生的频度,从而在分摊意义下保证整体的高效率
更准确地, Tarjan 等人采用势能分析法( potential analysis)也已证明,在改用“双层伸展”策略之后,伸展树的单次操作均可在分摊的 O(logn) 时间内完成
BZOJ 1588 [HNOI2002]营业额统计
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>
#include <cctype>
#include <bitset>
#include <ctime>
using namespace std;
#define REP(i, n) for (int i = 0; i < (n); ++i)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef pair<int, int> Pair;
const ull mod = 1e9 + 7;
const int INF = 0x7fffffff;
const int maxn = 1e5;
int son[maxn][2], pre[maxn], key[maxn], root, size;
void New_Node(int &r, int father, int x);
bool insert(int x);
void Rotate(int x, int kind);
void Splay(int x, int goal);
int Succ(int x);
int Pred(int x);
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
int n, num, ans = 0;
root = size = 0;
scanf("%d", &n);
scanf("%d", &num);
ans += num;
insert(num);
--n;
while (n--) {
scanf("%d", &num);
if (insert(num)) {
int pre = Pred(root);
int next = Succ(root);
if (pre == INF) {
ans += next - num;
} else if (next == INF) {
ans += num - pre;
} else {
ans += min(next-num, num-pre);
}
}
}
printf("%d\\n", ans);
return 0;
}
int Pred(int x)
{
int lmax = son[x][0];
if (lmax == 0) {
return INF;
}
while (son[lmax][1]) {
lmax = son[lmax][1];
}
return key[lmax];
}
int Succ(int x)
{
int rmin = son[x][1];
if (rmin == 0) {
return INF;
}
while (son[rmin][0]) {
rmin = son[rmin][0];
}
return key[rmin];
}
void Splay(int x, int goal)
{
while (pre[x] != goal) {
if (pre[pre[x]] == goal) {
Rotate(x, son[pre[x]][0] == x);
} else {
int y = pre[x];
int kind = son[pre[y]][0] == y;
if (son[y][kind] == x) {
Rotate(x, !kind);
Rotate(x, kind);
} else {
Rotate(y, kind);
Rotate(x, kind);
}
}
}
if (goal == 0) {
root = x;
}
}
void Rotate(int x, int kind)
{
int y = pre[x];
son[y][!kind] = son[x][kind];
pre[son[x][kind]] = y;
if (pre[y]) {
son[pre[y]][son[pre[y]][1] == y] = x;
}
pre[x] = pre[y];
son[x][kind] = y;
pre[y] = x;
}
bool insert(int x)
{
int pos = root;
while (son[pos][x > key[pos]]) {
if (key[pos] == x) {
Splay(pos, 0);
return false;
}
pos = son[pos][x > key[pos]];
}
New_Node(son[pos][x > key[pos]], pos, x);
Splay(size, 0);
return true;
}
void New_Node(int &r, int father, int x)
{
r = ++size;
pre[r] = father;
key[r] = x;
son[r][0] = son[r][1] = 0;
}BZOJ 1503 [NOI2004]郁闷的出纳员
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>
#include <cctype>
#include <bitset>
#include <ctime>
using namespace std;
#define REP(i, n) for (int i = 0; i < (n); ++i)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef pair<int, int> Pair;
const ull mod = 1e9 + 7;
const int INF = 0x7fffffff;
const int maxn = 1e5;
struct splay {
int son[maxn][2], pre[maxn], key[maxn], sum[maxn], root, size;
void Init();
void New_Node(int &r, int father, int x);
void insert(int x);
int remove(int x);
int find_by_order(int k);
void Rotate(int x, int kind);
void Splay(int x, int goal);
int Succ(int x);
int find(int x);
};
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
int n, Min, k, adjust = 0, ans = 0;
splay tree;
tree.Init();
char cmd[1];
scanf("%d %d", &n, &Min);
while (n--) {
scanf("%s %d", cmd, &k);
if (cmd[0] == 'I') {
if (k >= Min) {
tree.insert(k - adjust);
}
} else if (cmd[0] == 'A') {
adjust += k;
} else if (cmd[0] == 'S') {
adjust -= k;
ans += tree.remove(tree.Succ(Min - adjust));
} else {
int sum = tree.sum[tree.root];
if (k > (sum - 2)) {
printf("-1\\n");
} else {
printf("%d\\n", tree.find_by_order(sum - 1 - k) + adjust);
}
}
}
printf("%d\\n", ans);
return 0;
}
void splay::Init()
{
size = root = 0;
New_Node(root, 0, -INF);
New_Node(son[root][1], root, INF);
sum[root] = 2;
}
int splay::find_by_order(int k)
{
int pos = root;
while (sum[son[pos][0]] != k) {
if (sum[son[pos][0]] > k) {
pos = son[pos][0];
} else {
k -= (sum[son[pos][0]] + 1);
pos = son[pos][1];
}
}
Splay(pos, 0);
return key[pos];
}
int splay::Succ(int x)
{
int pos = root, Min = INF;
while (pos) {
if (key[pos] == x) {
return x;
}
if (key[pos] > x) {
Min = min(Min, key[pos]);
}
pos = son[pos][x > key[pos]];
}
return Min;
}
int splay::find(int x)
{
int pos = root, ret = 0;
while (pos) {
if (key[pos] == x) {
ret = pos;
}
pos = son[pos][x > key[pos]];
}
return ret;
}
int splay::remove(int x)
{
int pos = find(x);
Splay(1, 0);
Splay(pos, 1);
int ret = sum[son[pos][0]];
son[pos][0] = 0;
Splay(pos, 0);
return ret;
}
void splay::Splay(int x, int goal)
{
while (pre[x] != goal) {
if (pre[pre[x]] == goal) {
Rotate(x, son[pre[x]][0] == x);
} else {
int y = pre[x];
int kind = son[pre[y]][0] == y;
if (son[y][kind] == x) {
Rotate(x, !kind);
Rotate(x, kind);
} else {
Rotate(y, kind);
Rotate(x, kind);
}
}
}
sum[x] = sum[son[x][0]] + sum[son[x][1]] + 1;
if (goal == 0) {
root = x;
}
}
void splay::Rotate(int x, int kind)
{
int y = pre[x];
son[y][!kind] = son[x][kind];
pre[son[x][kind]] = y;
if (pre[y]) {
son[pre[y]][son[pre[y]][1] == y] = x;
}
pre[x] = pre[y];
son[x][kind] = y;
pre[y] = x;
sum[y] = sum[son[y][0]] + sum[son[y][1]] + 1;
}
void splay::insert(int x)
{
int pos = root;
while (son[pos][x > key[pos]]) {
pos = son[pos][x > key[pos]];
}
New_Node(son[pos][x > key[pos]], pos, x);
Splay(size, 0);
}
void splay::New_Node(int &r, int father, int x)
{
r = ++size;
pre[r] = father;
key[r] = x;
sum[r] = 1;
son[r][0] = son[r][1] = 0;
}#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>
#include <cctype>
#include <bitset>
#include <ctime>
using namespace std;
#define REP(i, n) for (int i = 0; i < (n); ++i)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef pair<int, int> Pair;
const ull mod = 1e9 + 7;
const int INF = 0x7fffffff;
const int maxn = 1e5;
struct splay {
int son[maxn][2], pre[maxn], key[maxn], sum[maxn], root, size;
void Init();
void New_Node(int &r, int father, int x);
void insert(int x);
int remove(int x);
int find_by_order(int k);
void Rotate(int x, int kind);
void Splay(int x, int goal);
int Succ(int x);
int find(int x);
};
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
int n, Min, k, adjust = 0, ans = 0;
splay tree;
tree.Init();
char cmd[1];
scanf("%d %d", &n, &Min);
while (n--) {
scanf("%s %d", cmd, &k);
if (cmd[0] == 'I') {
if (k >= Min) {
tree.insert(k - adjust);
}
} else if (cmd[0] == 'A') {
adjust += k;
} else if (cmd[0] == 'S') {
adjust -= k;
ans += tree.remove(tree.Succ(Min - adjust));
} else {
int sum = tree.sum[tree.root];
if (k > sum) {
printf("-1\\n");
} else {
printf("%d\\n", tree.find_by_order(sum + 1 - k) + adjust);
}
}
}
printf("%d\\n", ans);
return 0;
}
void splay::Init()
{
size = root = 0;
}
int splay::find_by_order(int k)
{
int pos = root;
while (sum[son[pos][0]] + 1 != k) {
if (sum[son[pos][0]] + 1 > k) {
pos = son[pos][0];
} else {
k -= (sum[son[pos][0]] + 1);
pos = son[pos][1];
}
}
Splay(pos, 0);
return key[pos];
}
int splay::Succ(int x)
{
int pos = root, Min = INF;
while (pos) {
if (key[pos] == x) {
return x;
}
if (key[pos] > x) {
Min = min(Min, key[pos]);
}
pos = son[pos][x > key[pos]];
}
return Min;
}
int splay::find(int x)
{
int pos = root, ret = 0;
while (pos) {
if (key[pos] == x) {
ret = pos;
}
pos = son[pos][x > key[pos]];
}
return ret;
}
int splay::remove(int x)
{
int pos = find(x), ret = 0;
if (pos == 0) {
ret = sum[root];
size = root = 0;
memset(son, 0, sizeof(son));
} else {
Splay(pos, 0);
ret = sum[son[pos][0]];
son[pos][0] = 0;
Splay(pos, 0);
}
return ret;
}
void splay::Splay(int x, int goal)
{
while (pre[x] != goal) {
if (pre[pre[x]] == goal) {
Rotate(x, son[pre[x]][0] == x);
} else {
int y = pre[x];
int kind = son[pre[y]][0] == y;
if (son[y][kind] == x) {
Rotate(x, !kind);
Rotate(x, kind);
} else {
Rotate(y, kind);
Rotate(x, kind);
}
}
}
sum[x] = sum[son[x][0]] + sum[son[x][1]] + 1;
if (goal == 0) {
root = x;
}
}
void splay::Rotate(int x, int kind)
{
int y = pre[x];
son[y][!kind] = son[x][kind];
pre[son[x][kind]] = y;
if (pre[y]) {
son[pre[y]][son[pre[y]][1] == y] = x;
}
pre[x] = pre[y];
son[x][kind] = y;
pre[y] = x;
sum[y] = sum[son[y][0]] + sum[son[y][1]] + 1;
}
void splay::insert(int x)
{
int pos = root;
while (son[pos][x > key[pos]]) {
pos = son[pos][x > key[pos]];
}
New_Node(son[pos][x > key[pos]], pos, x);
Splay(size, 0);
}
void splay::New_Node(int &r, int father, int x)
{
r = ++size;
pre[r] = father;
key[r] = x;
sum[r] = 1;
son[r][0] = son[r][1] = 0;
}BZOJ 1208 [HNOI2004]宠物收养所
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>
#include <cctype>
#include <bitset>
#include <ctime>
using namespace std;
#define REP(i, n) for (int i = 0; i < (n); ++i)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef pair<int, int> Pair;
const int mod = 1000000;
const int INF = 0x3fffffff;
const int maxn = 1e5;
struct splay {
int son[maxn][2], pre[maxn], key[maxn], sum[maxn], root, size;
void Init();
void New_Node(int &r, int father, int x);
void insert(int x);
void remove(int x);
void Rotate(int x, int kind);
void Splay(int x, int goal);
int Pred(int x);
int Succ(int x);
int find(int x);
};
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
splay tree;
int n, a, b, ans = 0, num[2];
num[0] = num[1] = 0;
tree.Init();
scanf("%d", &n);
while (n--) {
scanf("%d %d", &a, &b);
if (num[!a] == 0) {
++num[a];
tree.insert(b);
} else {
int pre = tree.Pred(b);
int next = tree.Succ(b);
if (b - pre <= next - b) {
tree.remove(pre);
ans += b - pre;
} else {
tree.remove(next);
ans += next - b;
}
ans %= mod;
--num[!a];
}
}
printf("%d\\n", ans);
return 0;
}
void splay::Init()
{
size = root = 0;
New_Node(root, 0, -INF);
New_Node(son[root][1], root, INF);
}
int splay::find(int x)
{
int pos = root;
while (pos) {
if (key[pos] == x) {
return pos;
}
pos = son[pos][x > key[pos]];
}
return 0;
}
int splay::Pred(int x)
{
int pos = root, Max = -INF;
while (pos) {
if (key[pos] == x) {
return x;
}
if (key[pos] < x) {
Max = max(Max, key[pos]);
}
pos = son[pos][x > key[pos]];
}
return Max;
}
int splay::Succ(int x)
{
int pos = root, Min = INF;
while (pos) {
if (key[pos] == x) {
return x;
}
if (key[pos] > x) {
Min = min(Min, key[pos]);
}
pos = son[pos][x > key[pos]];
}
return Min;
}
void splay::remove(int x)
{
int pos = find(x);
Splay(pos, 0);
int t = son[pos][1];
while (son[t][0]) {
t = son[t][0];
}
Splay(t, root);
son[t][0] = son[root][0];
pre[son[root][0]] = t;
pre[t] = 0;
root = t;
}
void splay::Splay(int x, int goal)
{
while (pre[x] != goal) {
if (pre[pre[x]] == goal) {
Rotate(x, son[pre[x]][0] == x);
} else {
int y = pre[x];
int kind = son[pre[y]][0] == y;
if (son[y][kind] == x) {
Rotate(x, !kind);
Rotate(x, kind);
} else {
Rotate(y, kind);
Rotate(x, kind);
}
}
}
sum[x] = sum[son[x][0]] + sum[son[x][1]] + 1;
if (goal == 0) {
root = x;
}
}
void splay::Rotate(int x, int kind)
{
int y = pre[x];
son[y][!kind] = son[x][kind];
pre[son[x][kind]] = y;
if (pre[y]) {
son[pre[y]][son[pre[y]][1] == y] = x;
}
pre[x] = pre[y];
son[x][kind] = y;
pre[y] = x;
sum[y] = sum[son[y][0]] + sum[son[y][1]] + 1;
}
void splay::insert(int x)
{
int pos = root;
while (son[pos][x > key[pos]]) {
pos = son[pos][x > key[pos]];
}
New_Node(son[pos][x > key[pos]], pos, x);
Splay(size, 0);
}
void splay::New_Node(int &r, int father, int x)
{
r = ++size;
pre[r] = father;
key[r] = x;
sum[r] = 1;
son[r][0] = son[r][1] = 0;
}BZOJ 1500 [NOI2005]维修数列
参考:http://www.cnblogs.com/kuangbin/archive/2013/08/28/3287822.html
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>
#include <cctype>
#include <bitset>
#include <ctime>
using namespace std;
#define REP(i, n) for (int i = 0; i < (n); ++i)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef pair<int, int> Pair;
const ull mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int maxn = 5e5 + 10;
struct splay {
int pre[maxn], son[maxn][2], key[maxn], size[maxn];
int sum[maxn], reverse[maxn], same[maxn];
int lx[maxn], rx[maxn], mx[maxn];
int root, Count;
void Init(void);
void New_Node(int &r, int father, int _key);
void Build(int &a, int low, int high, int father);
void Push_Up(int r);
void Push_Down(int r);
void Update_Rev(int r);
void Update_Same(int r, int _key);
void Rotate(int a, int kind);
void Splay(int r, int goal);
void erase(int r);
void insert(int pos, int tot);
void remove(int pos, int tot);
int find_by_order(int r, int k);
void Make_Same(int pos, int tot, int c);
void Reverse(int pos, int tot);
int Get_Sum(int pos, int tot);
int Get_MaxSum(int pos, int tot);
};
splay tree;
int num[maxn];
int Stack[maxn], depth = 0;
char cmd[20];
int N, M, x, y, z;
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
scanf("%d %d", &N, &M);
tree.Init();
while (M--) {
scanf("%s", cmd);
if (strcmp(cmd, "INSERT") == 0) {
scanf("%d %d", &x, &y);
tree.insert(x, y);
} else if (strcmp(cmd, "DELETE") == 0) {
scanf("%d %d", &x, &y);
tree.remove(x, y);
} else if (strcmp(cmd, "MAKE-SAME") == 0) {
scanf("%d %d %d", &x, &y, &z);
tree.Make_Same(x, y, z);
} else if (strcmp(cmd, "REVERSE") == 0) {
scanf("%d %d", &x, &y);
tree.Reverse(x, y);
} else if (strcmp(cmd, "GET-SUM") == 0) {
scanf("%d %d", &x, &y);
printf("%d\\n", tree.Get_Sum(x, y));
} else {
printf("%d\\n", tree.Get_MaxSum(1, tree.size[tree.root]-2));
}
}
return 0;
}
int splay::Get_MaxSum(int pos, int tot)
{
Splay(find_by_order(root, pos), 0);
Splay(find_by_order(root, pos+tot+1), root);
return mx[son[son[root][1]][0]];
}
int splay::Get_Sum(int pos, int tot)
{
Splay(find_by_order(root, pos), 0);
Splay(find_by_order(root, pos+tot+1), root);
return sum[son[son[root][1]][0]];
}
void splay::Reverse(int pos, int tot)
{
Splay(find_by_order(root, pos), 0);
Splay(find_by_order(root, pos+tot+1), root);
Update_Rev(son[son[root][1]][0]);
Push_Up(son[root][1]);
Push_Up(root);
}
void splay::Make_Same(int pos, int tot, int c)
{
Splay(find_by_order(root, pos), 0);
Splay(find_by_order(root, pos+tot+1), root);
Update_Same(son[son[root][1]][0], c);
Push_Up(son[root][1]);
Push_Up(root);
}
void splay::remove(int pos, int tot)
{
Splay(find_by_order(root, pos), 0);
Splay(find_by_order(root, pos+tot+1), root);
erase(son[son[root][1]][0]);
pre[son[son[root][1]][0]] = 0;
son[son[root][1]][0] = 0;
Push_Up(son[root][1]);
Push_Up(root);
}
void splay::erase(int r)
{
if (r == 0) {
return;
}
Stack[++depth] = r;
erase(son[r][0]);
erase(son[r][1]);
}
void splay::insert(int pos, int tot)
{
for (int i = 0; i < tot; ++i) {
scanf("%d", &num[i]);
}
Splay(find_by_order(root, pos+1), 0);
Splay(find_by_order(root, pos+2), root);
Build(son[son[root][1]][0], 0, tot-1, son[root][1]);
Push_Up(son[root][1]);
Push_Up(root);
}
void splay::Splay(int r, int goal)
{
Push_Down(r);
while (pre[r] != goal) {
if (pre[pre[r]] == goal) {
Push_Down(pre[r]);
Push_Down(r);
Rotate(r, son[pre[r]][0] == r);
} else {
Push_Down(pre[pre[r]]);
Push_Down(pre[r]);
Push_Down(r);
int b = pre[r];
int kind = son[pre[b]][0] == b;
if (son[b][kind] == r) {
Rotate(r, !kind);
Rotate(r, kind);
} else {
Rotate(b, kind);
Rotate(r, kind);
}
}
}
Push_Up(r);
if (goal == 0) {
root = r;
}
}
void splay::Rotate(int a, int kind)
{
int b = pre[a];
Push_Down(b);
Push_Down(a);
son[b][!kind] = son[a][kind];
pre[son[a][kind]] = b;
if (pre[b]) {
son[pre[b]][son[pre[b]][1] == b] = a;
}
pre[a] = pre[b];
son[a][kind] = b;
pre[b] = a;
Push_Up(b);
}
int splay::find_by_order(int r, int k)
{
Push_Down(r);
int lsize = size[son[r][0]];
if (k <= lsize) {
return find_by_order(son[r][0], k);
} else if (k > lsize+1) {
return find_by_order(son[r][1], k - lsize - 1);
}
return r;
}
void splay::Push_Down(int r)
{
if (same[r]) {
Update_Same(son[r][0], key[r]);
Update_Same(son[r][1], key[r]);
same[r] = 0;
}
if (reverse[r]) {
Update_Rev(son[r][0]);
Update_Rev(son[r][1]);
reverse[r] = 0;
}
}
void splay::Update_Same(int r, int _key)
{
if (r == 0) {
return;
}
key[r] = _key;
sum[r] = _key * size[r];
lx[r] = rx[r] = mx[r] = max(_key, sum[r]);
same[r] = 1;
}
void splay::Update_Rev(int r)
{
if (r == 0) {
return;
}
swap(son[r][0], son[r][1]);
swap(lx[r], rx[r]);
reverse[r] ^= 1;
}
void splay::New_Node(int &r, int father, int _key)
{
if (depth) {
r = Stack[depth--];
} else {
r = ++Count;
}
pre[r] = father;
son[r][1] = son[r][0] = 0;
key[r] = _key;
sum[r] = _key;
reverse[r] = same[r] = 0;
lx[r] = rx[r] = mx[r] = _key;
size[r] = 1;
}
void splay::Init()
{
root = Count = depth = 0;
son[root][0] = son[root][1] = pre[root] = size[root] = 0;
same[root] = reverse[root] = sum[root] = key[root] = 0;
lx[root] = rx[root] = mx[root] = -INF;
New_Node(root, 0, -1);
New_Node(son[root][1], root, -1);
for (int i = 0; i < N; ++i) {
scanf("%d", &num[i]);
}
Build(son[son[root][1]][0], 0, N-1, son[root][1]);
Push_Up(son[root][1]);
Push_Up(root);
}
void splay::Build(int &a, int low, int high, int father)
{
if (low > high) {
return;
}
int mid = (low + high) / 2;
New_Node(a, father, num[mid]);
Build(son[a][0], low, mid-1, a);
Build(son[a][1], mid+1, high, a);
Push_Up(a);
}
void splay::Push_Up(int r)
{
int lson = son[r][0], rson = son[r][1];
size[r] = size[lson] + size[rson] + 1;
sum[r] = sum[lson] + sum[rson] + key[r];
lx[r] = max(lx[lson], sum[lson] + key[r] + max(0, lx[rson]));
rx[r] = max(rx[rson], sum[rson] + key[r] + max(0, rx[lson]));
mx[r] = max(0, rx[lson]) + key[r] + max(0, lx[rson]);
mx[r] = max(mx[r], max(mx[lson], mx[rson]));
}splay 题集:
http://www.cnblogs.com/kane0526/archive/2012/12/31/2840757.html
http://blog.csdn.net/acm_cxlove/article/details/7815019
以上是关于Splay Tree(伸展树)的主要内容,如果未能解决你的问题,请参考以下文章