实验一

Posted 2020-08-09

1、用你的计算机上的压缩工具来压缩不同文件。研究原文件的大小和类型对于压缩文件与原文件大小之比的影响。

答：经试验发现原文件的大小和类型对于压缩文件与原文件大小之比有影响，特别是TXT类型的，压缩文件与原文件大小之基本是百分之五十，如果压缩的文件为".jpg"".rm"".rmvb"".mp3""3gp""rar""zip""".exe"文件,这些文件本身就是压缩后的文件.再压缩大小不会变化。其他类型的文件压缩之后大小变化不大，文件越大能压缩的就多。

2、 从一本通俗杂志中摘录几段文字，并删除所有不会影响理解的文字，实现压缩。例如，在“This is the dog that belongs to my friend”中，删除is、the、that和to之后，仍然能传递相同的意思。用被删除的单词数与原文本的总单词数之比来衡量文本中的冗余度。用一本技术期刊中的文字来重复这一试验。对于摘自不同来源的文字，我们能否就其冗余度做出定量论述？

答：冗余度它表征源信息率的重复程度，是描述信源客观统计特性的一个物理量。也可以说是从多余的一个量，通俗的讲就是数据的重复度。它不影响数据的完整，也正是因为这一个多余量的存在，才能对其信源进行压缩，压缩后不会影响传递信息。

我们不能对其冗余度做出定量论述，假如在文学写作中使用到一些重叠词：缠缠绵绵 凄凄惨惨，冷冷清清等等，去掉冗余也可以表达这个意思，但是却少了那种意境。所以我认为不能。(信源=信息+冗余度。)

编写一段程序，从包括26个字母的符号集{a,b,...,z}中随机选择字母，组成100个四字母单词，这些单词中有多少是有意义的？

#include<iostream>

using namespace std;

int main()

{  

   int word,i,j;

    char n[100][5];

    for(i=0;i<100;i++)  

   {      

   for(j=0;j<4;j++)  

       {      

       word=rand()%26;     

        n[i][j]=word+‘a‘;    

     }        

n[i][4]=‘\0‘;       

  cout<<i+1<<‘:‘<<n[i]<<"\t";   

  }    

return 0;

}

 

 

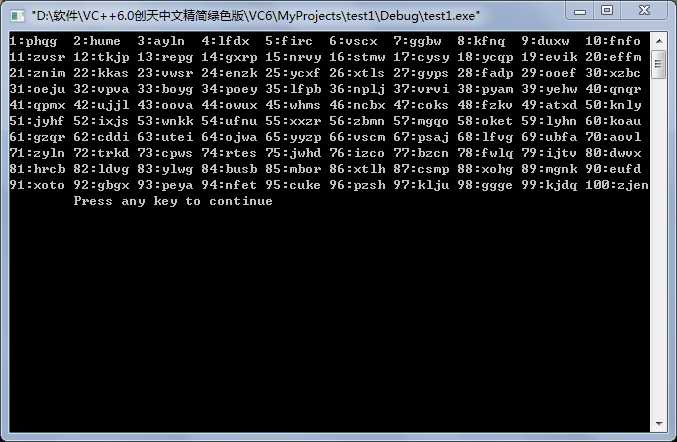
有2个   ①Hume 译文：n. 休姆（人名，姓氏）   ②poey 译文：波埃