计算机算法设计与分析之棋盘覆盖问题

Posted 2020-06-13

一、引子

近期又又一次上了算法课，如今想来有点汗颜。大学期间已经学习了一个学期。到如今却依旧感觉仅仅是把老师讲过的题目弄懂了，并没有学到算法的一些好的分析方法和思路，碰到一个新的问题后往往感觉非常棘手，痛定思痛之后认为还是好好再学习一遍。争取能理解透彻每种算法的思路和核心，同一时候也劝诫各位同行们做事要脚踏实地，不能应付老师的作业，最后吃亏的还是自己啊。

二、棋盘覆盖问题

       在一个由2^k *2^k个方格组成的棋盘中，恰有一个方格与其它方格不同。称该方格为一特殊方格，且称该棋盘
为一特殊棋盘。现有四种L型骨牌例如以下图所看到的，要用这四种骨牌覆盖棋盘上除特殊方格之外的其它全部格子，且两个L型骨牌不能相互覆盖。

      

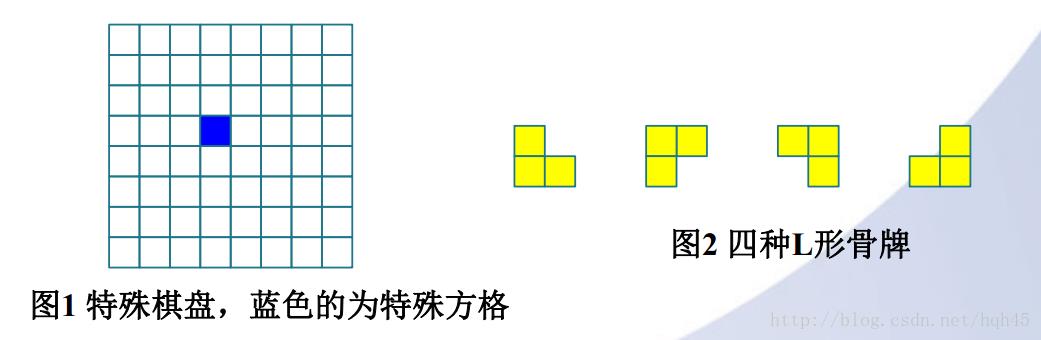
三、解题思路

对于复杂问题。我们的一种经常使用思路是简化问题，简化到我们能一眼能看出问题的答案，这里也一样。

当k=1时，问题简化为一个2*2的棋盘的问题。因为仅仅有四个格子，且含有一个特殊格子，这样就仅仅能用一个相应的L型骨牌覆盖了。问题已经非常easy了。

在此我们又一次定义四种L型骨牌：

在棋盘中，我们採用（行。列）来表示某一个格子，由于(x,y)这样的表示对图像处理的人来说是有歧义的，我们更愿意觉得第一维是行，第二维是列。

如果在2*2的棋盘中。特殊格子出如今(0,0)这个位子上，则我们要使用0型骨牌覆盖其余位置，同理，如果特殊格子出如今(0,1)这个位置上，我们要用1型骨牌覆盖其余位置。更具有一般性的。如果特殊格子出如今2*2的(row,col)这个位置上，我们要使用row*2+col型骨牌覆盖其余位置，row和col都是从0開始索引的。

当k=2时，问题变成了一个4*4的棋盘问题，这个时候问题略显复杂，我们就想啊。假设能够把它变成2*2的棋盘问题多好啊，好吧，我们就把它分成四个2*2的子棋盘，对于那个有特殊的格子的2*2子棋盘，非常快变能够解决，剩下的三个呢？让我们画出图好好看看。

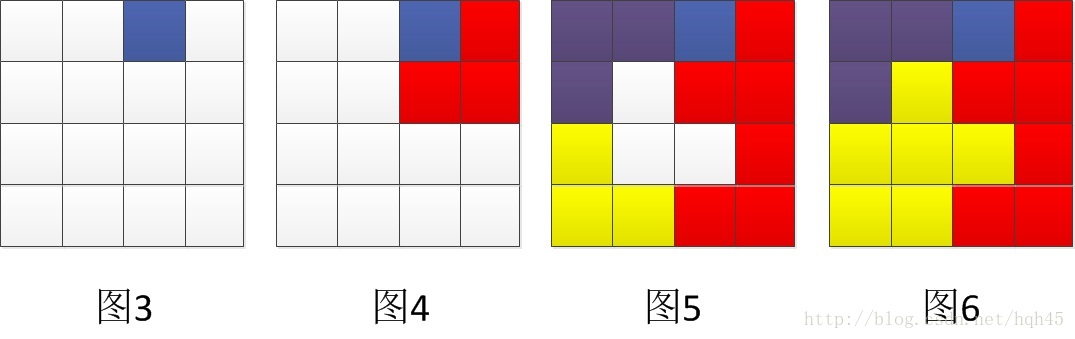
如果特殊格子出如今(0,2)这个位置，如图3所看到的，那么对于含有特殊格子的右上角的子棋盘我们用0型骨牌填充，如图4。那么剩余的三个子棋盘呢，这个时候我们发现左上角仅仅能覆盖3型和2型，其它两种会有剩余空格。如果覆盖2型骨牌，后面的左下角必定无法全然覆盖（自己能够试一下），则仅仅能使用3型骨牌覆盖，以此类推，我们也能够覆盖左下角和右下角此时仅仅剩三个格子没有覆盖，如图5所看到的。

如今细致观測剩余的三个格子，我们发现他们都是分开在三个子棋盘里。那么这些空格子在子棋盘中是无法直接被覆盖的，由于每一个子棋盘仅仅剩一个空格子了，我们是不是能够把这个空格子当成一个特殊格子，这样四个子棋盘都是含有一个特殊格子的小棋盘。这样原问题就变成了四个相同的子问题，再求解了每一个子棋盘后，我们再对三个假的子棋盘格子进行覆盖（如图6）。

那么怎样选择空格作为子棋盘的特殊格子呢。通过观察我们发现，对于含有特殊格子的子棋我们不用指定特殊格子，对于剩下三个子棋盘，我们指定四个子棋盘的交界处的格子作为特殊格子。

四、归纳

如今我们归纳总结一下我们的解题方案：首先将大棋盘四等分分成四个2^(k-1)*2^(k-1)的子棋盘。然后对没有特殊格子的子棋盘指定假的特殊格子的位置。将原问题分解成四个子问题进行求解。当然四个子问题可能还不能直接求解，可能还有继续递归求解。如果已经求解了四个子问题，我们应该用特定的L型骨牌覆盖三个假的特殊格子，至此整个大棋盘已经求解完毕。

我们会想整个求解过程，首先把问题简化，简化到直接看出答案的地步，然后分析略微复杂一点的情况，总结规律，运用分治的思想。将问题化解成四个子问题，分别求解四个子问题，在求解子问题的过程中可能还会有子问题。不断的递归求解，终于每一个子问题解决。大问题也解决。

五、代码实现

#include <iostream>
#include<memory.h>
using namespace std;
int **chessBoard;
int k=1;
int length=0;
int blueRow=-1;
int blueCol=-1;
void init();
void fillBoard(int **_chessBoard,int r,int c,int type);
void fillChessBoard(int **_chessBoard,int k,int blue_row,int blue_col,int baseRow,int baseCol);
void output(int **_chessBoard);
int main()
{
    init();

    fillChessBoard(chessBoard,k,blueRow,blueCol,0,0);
    output(chessBoard);

    for(int i=0;i<length;i++)
    {
        delete [] chessBoard[i];
    }
    delete chessBoard;
    return 0;
}
void init()
{
    cout<<"please input number k:"<<endl;
    cin>>k;
    cout<<"please input blue grid coordinate:row column"<<endl;
    cin>>blueRow>>blueCol;

    length=(1<<k);//长和宽均为2^k
    //动态分配2^k数组
    chessBoard=new int*[length];
    for(int i=0;i<length;i++)
    {
        chessBoard[i]=new int[length];
        //初始化为-1
        memset(chessBoard[i],-1,length*sizeof(int));
    }
    chessBoard[blueRow][blueCol]=4;
}
void output(int **_chessBoard)
{
    for(int i=0;i<length;i++)
    {
        for(int j=0;j<length;j++)
        {
            cout<<" "<<_chessBoard[i][j];
        }
        cout<<endl;
    }
    cout<<endl;
}
void fillBoard(int **_chessBoard,int r,int c,int type)
{
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            if((i*2+j)!=type)
            {
                if(_chessBoard[r+i][c+j]!=-1)
                    cout<<"error"<<endl;
                _chessBoard[r+i][c+j]=type;
            }
        }
    }
}
void fillChessBoard(int **_chessBoard,int level,int blue_row,int blue_col,int baseRow,int baseCol)
{
    if(level==1)
    {
        int type=(blue_row<<1)+blue_col;
        fillBoard (_chessBoard,baseRow,baseCol,type);

    }else
    {
        //否则进行四等分，中间连接处自行填充

        //新的四分格的宽度
        int new_length=1<<(level-1);
        int type=(blue_row/new_length)*2+blue_col/new_length;
        for(int r=0;r<2;r++)
        {
            for(int c=0;c<2;c++)
            {
                if((r*2+c)==type)
                {
                    fillChessBoard (_chessBoard,level-1,blue_row-r*new_length,blue_col-c*new_length,r*new_length+baseRow,c*new_length+baseCol);
                }
                else
                {
                    fillChessBoard (_chessBoard,level-1,(new_length-1)*(1-r),(new_length-1)*(1-c),r*new_length+baseRow,c*new_length+baseCol);
                }
            }
        }
        fillBoard (_chessBoard,baseRow+new_length-1,baseCol+new_length-1,type);
    }

}

六、代码解释

程序输入为棋盘大小的參数k、特殊格子的行和列，输出为整个棋盘，我们用4表示特殊格子，0-3分别表示0-3型的L型骨牌。

fillBoard()函数是使用某种L型骨牌覆盖棋盘的函数。fillChessBoard()是递归求解整个问题的函数，输入为棋盘指针。參数level也就是k。blue_row,blue_col是特殊格子在子棋盘的坐标系的位置，baseRow和baseCol是子棋盘的(0,0)点在整个的大棋盘中的坐标。

持续跟新中。敬请关注