33. Search in Rotated Sorted Array (Array;Divide-and-Conquer)

Posted 2020-08-09 joannae

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

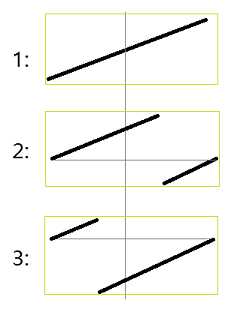
思路: 改动的二分法。有三种情况：正序、右侧rotate、左侧rotate。三种情况分别讨论。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        return binarySearch(nums,0,nums.size()-1, target);
    }
    
    int binarySearch(vector<int>& nums, int start, int end, int target){
        if(start>end){
            return -1;
        }
        
        int mid = start+ ((end-start)>>1);
        if(nums[mid]==target) return mid;
        
        //正序
        if(nums[mid]>=nums[start] && nums[mid]<nums[end]){ //mid可能会=start，所以这里要用>=
            if(target < nums[mid]) return binarySearch(nums,start,mid-1,target); //mid+1或-1,每次至少舍弃一个数
            else return binarySearch(nums,mid+1,end,target);
        }
        
        //右侧rotate
        else if(nums[mid]>=nums[start] && nums[mid]>nums[end]){
            if(target>=nums[start] && target<nums[mid]) return binarySearch(nums,start,mid-1,target);
            else return binarySearch(nums,mid+1,end,target);
        }
        
        //左侧rotate
        else{
            if(target>=nums[start] || target<nums[mid]) return binarySearch(nums,start,mid-1,target);
            else return binarySearch(nums,mid+1,end,target);
        }
    }
};