51nod1258 序列求和V4

Posted 2020-08-09 ccz181078

T(n) = n^k，S(n) = T(1) + T(2) + ...... T(n)。给出n和k，求S(n)。

 

例如k = 2，n = 5，S(n) = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55。

由于结果很大，输出S(n) Mod 1000000007的结果即可。

Input

第1行：一个数T，表示后面用作输入测试的数的数量。（1 <= T <= 500)
第2 - T + 1行：每行2个数，N, K中间用空格分割。(1 <= N <= 10^18, 1 <= K <= 50000)

Output

共T行，对应S(n) Mod 1000000007的结果。

设伯努利数第i项为B[i]，则有结论

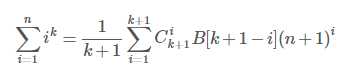
由于伯努利数的指数生成函数为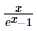，化简得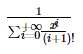，计算其在模x⁵⁰⁰⁰¹意义下，系数模1e9+7的结果即得到B[0..50000] mod (1e9+7)

由于模数较大，计算多项式逆元可以用倍增+（三模数ntt+CRT合并（每次倍增需15次ntt）或分段fft（一般写法每次倍增需12次dft）），复杂度为O(50000log50000)，常数较大

#include<cstdio>
#include<cmath>
#include<algorithm>
typedef long double ld;
typedef long long i64;
const ld pi=3.1415926535897932384626433832795l;
const int P=1000000007,M=31623;
struct cplx{
    ld a,b;
    cplx(ld _a=0.l,ld _b=0.l):a(_a),b(_b){}
    cplx operator+(cplx x){return cplx(a+x.a,b+x.b);}
    cplx operator-(cplx x){return cplx(a-x.a,b-x.b);}
    cplx operator*(cplx x){return cplx(a*x.a-b*x.b,a*x.b+b*x.a);}
    cplx operator~(){return cplx(a,-b);}
}w[2][131072],A[131072],B[131072],C[131072],D[131072];
int N,X,r[131072];
void dft(cplx*a,int t){
    for(int i=0;i<N;++i)if(i>r[i])std::swap(a[i],a[r[i]]);
    for(int i=1;i<N;i<<=1){
        for(int j=0,v=65536/i;j<N;j+=i<<1){
            cplx*b=a+j,*c=b+i;
            for(int k=0,p=0;k<i;++k,p+=v){
                cplx x=b[k],y=c[k]*w[t][p];
                b[k]=x+y;
                c[k]=x-y;
            }
        }
    }
    if(t)for(int i=0;i<N;++i)a[i].a/=N;
}
int pow(int a,int n){
    int v=1;
    for(;n;n>>=1){
        if(n&1)v=i64(v)*a%P;
        a=i64(a)*a%P;
    }
    return v;
}
int fac[50007]={1},fiv[50007]={1},v1[50007],v2[50007],v3[50007],b[50007];
void calc(int n){
    if(n==1){
        v2[0]=1;
        return;
    }
    int n1=n+1>>1;
    calc(n1);
    for(N=2,X=0;N<n*2;N<<=1,++X);
    for(int i=1;i<N;++i)r[i]=r[i>>1]>>1|(i&1)<<X;
    for(int i=0;i<n1;++i)A[i]=cplx(v2[i]/M),B[i]=cplx(v2[i]%M);
    for(int i=n1;i<N;++i)A[i]=B[i]=cplx();
    dft(A,0);dft(B,0);
    for(int i=0;i<N;++i){
        C[i]=B[i]*B[i];
        B[i]=A[i]*B[i];
        A[i]=A[i]*A[i];
    }
    dft(A,1);dft(B,1);dft(C,1);
    for(int i=0;i<n;++i)v3[i]=(i64(A[i].a+0.4999l)%P*(M*M)%P+i64(B[i].a+0.4999l)%P*2*M%P+i64(C[i].a+0.4999l))%P;
    for(int i=0;i<n;++i)A[i]=cplx(v3[i]/M),B[i]=cplx(v3[i]%M),C[i]=cplx(v1[i]/M),D[i]=cplx(v1[i]%M);
    for(int i=n;i<N;++i)A[i]=B[i]=C[i]=D[i]=cplx();
    dft(A,0);dft(B,0);dft(C,0);dft(D,0);
    for(int i=0;i<N;++i){
        cplx x=A[i]*D[i]+B[i]*C[i];
        A[i]=A[i]*C[i];
        C[i]=B[i]*D[i];
        B[i]=x;
    }
    dft(A,1);dft(B,1);dft(C,1);
    for(int i=0;i<n;++i){
        int x=(v2[i]*2ll+P-(i64(A[i].a+0.4999l)%P*(M*M)%P+i64(B[i].a+0.4999l)%P*M%P+i64(C[i].a+0.4999l)%P))%P;
        v2[i]=x<0?x+P:x;
    }
}
int _C(int n,int m){
    return fac[n]*1ll*fiv[m]%P*fiv[n-m]%P;
}
int main(){
    for(int i=0;i<131072;++i){
        w[0][i]=cplx(cos(pi*i/65536.l),sin(pi*i/65536.l));
        w[1][i]=~w[0][i];
    }
    for(N=2,X=0;N<111;N<<=1,++X);
    for(int i=1;i<N;++i)r[i]=r[i>>1]>>1|(i&1)<<X;
    for(int i=1;i<=50001;++i){
        fac[i]=1ll*fac[i-1]*i%P;
        fiv[i]=pow(fac[i],P-2);
    }
    for(int i=0;i<=50000;++i)v1[i]=fiv[i+1];
    calc(50001);
    for(int i=0;i<=50000;++i)b[i]=v2[i]*1ll*fac[i]%P;
    i64 n0,n;int T,k;
    for(scanf("%d",&T);T;--T){
        scanf("%lld%d",&n0,&k);
        int ans=0;
        n=(n0+1)%P;
        for(int i=1,pw=n;i<=k+1;++i,pw=1ll*pw*n%P){
            ans=(ans+1ll*_C(k+1,i)*b[k+1-i]%P*pw)%P;
        }
        ans=1ll*ans*pow(k+1,P-2)%P;
        if(ans<0)ans+=P;
        printf("%d\n",ans);
    }
    return 0;
}