数据结构和算法分析(11)树的简介
Posted MenAngel
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法分析(11)树的简介相关的知识,希望对你有一定的参考价值。
对于大量的数据,链表的线性访问时间太慢,不宜使用。我们介绍一种简单的数据结构,其大部分操作的平均时间为O(log N)。
(1)学习目标:
我们将要涉及到的数据结构叫做二叉查找树(binary search tree)。
我们将要了解如下内容:
1.了解树是如何用于实现几个流行的操作系统中的文件系统的; 2.看到树如何能够用来计算算术表达式的值; 3.如何指出利用树支持以O(log N)平均时间进行的各种搜索操作,以及如何细化得到最坏情况时间界O(log N)。我们还将讨论当数据被存在磁盘上时如何来实现这些操作。
(2)树的基础知识:
树的递归定义:
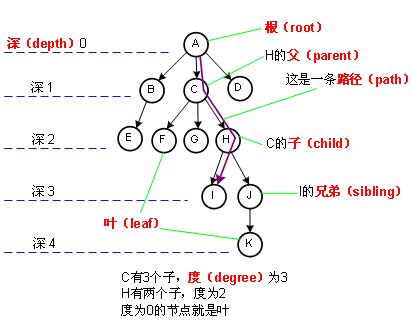
一棵树由称作根(root)的结点r以及0个或多个非空的(子)树T1,T2,T3......组成,这些子树中每一颗的根都来自根r的一条有向边(Edge)所连接。
2.1树的实现:
每一个结点的儿子树不确定时,可以进行如下定义:
typedef struct TreeNode *PtrToNode; struct TreeNode { ElementType Element; PtrToNode FirstChild; PtrToNode NextSibling; }

2.2树的遍历及应用:
树有很多应用,流行的用法之一是包括UNIX,VAX,VAX/VMS和DOS在内的许多常用操作系统中的目录结构:
在Unix文件系统每个目录还有一项指该向目录本身以及另一项指向该目录的父目录。因此严格来说,UNIX文件系统不是树,而是类树。
设我们想要得到目录中所有文件的名字。我们的输出格式是:深度为di的文件的名字将被第di此跳格缩进后打印出来:
static void ListDir(DirectoryOrFile D,int Depth) { if(D is a legitimate entry) { PrintName(D,Name); if(D is a directory) for each child,c,of D ListDir(C,Depth+1); } }//算法的核心例程 void ListDirectory(DirectoryOrFile D) { ListDir(D,0); }//驱动例程

输出文件通常用树的先序遍历(preorider traversal),而树的后续遍历通常用来计算该树所有文件占用的磁盘块的总数。
计算一个目录大小的例程:
static void SizeDirectory(DirectoryFile D) { int TotalSize; TotalSize=0; if(D is a legitimate Entry) { TotalSize=FileSize(D);//当当前是文件,不是目录时 if(D is a directory) for(each child,C, of D) TotalSize+=SizeDirectory(C); } return TotalSize; }
(3)二叉树:
定义:
二叉树(binary tree)是一棵树,每一个结点都不能有多于两个的儿子。

特点:
平均二叉树的深度要比N小得多,这个性质有时很重要。分析表明,这个平均深度为O(√N),而对于特殊的二叉树,即二叉查找树(binary search tree),其深度的平均值是O(log N)。
二叉树的结点声明:
typedef struct TreeNode *PtrToNode; typedef struct PtrToNode Tree; struct TreeNode { ElementType Element; Tree left; Tree right; };
(4)二叉树的应用:(表达式树)
二叉树有许多与搜索无关的重要应用。它的主要用途之一是在编译器的设计领域。
1 /***************构造表达式树***************/ 2 /* 3 1.输入中缀表达式先转化为后缀表达式; 4 2.根据后缀表达式构造树 5 3.分别以中序遍历法和后序遍历法遍历此树 6 */ 7 #include<stdio.h> 8 #include<stdlib.h> 9 #include<string.h> 10 11 #define EmptyTOS (-1) 12 #define MinStackSize 5 13 14 struct StackRecord{ 15 int Capacity;//能存元素最大量 16 int TopOfStack;//记录新插入的元素所在数组中的位置 17 char Array[30][5];//字符串数组,每个字符串的大小最多为5 18 }; 19 typedef struct StackRecord *Stack; 20 21 void MakeEmpty(Stack s){ 22 s->TopOfStack=EmptyTOS; 23 } 24 Stack CreateStack(int MaxElement){ 25 Stack s; 26 if(MaxElement<MinStackSize){ 27 printf("要创建的栈太小,应大于5。\\n"); 28 exit(0); 29 }else{ 30 s=malloc(sizeof(struct StackRecord)); 31 s->Capacity=MaxElement; 32 MakeEmpty(s); 33 } 34 return s; 35 } 36 //判断栈是否为空栈 37 int IsEmpty(Stack S){ 38 return S->TopOfStack==EmptyTOS; 39 } 40 //判断是否满了,当为1是满了,为0是表示未满 41 int IsFull(Stack S){ 42 if(S->TopOfStack+1>=S->Capacity){ 43 return 1; 44 }else 45 return 0; 46 } 47 //压栈 48 void Push(char *x,Stack S){ 49 if(IsFull(S)){ 50 printf("栈已经满了!\\n"); 51 }else{ 52 strcpy(S->Array[++S->TopOfStack],x); 53 } 54 } 55 //只获得头元素 56 char *Top(Stack S){ 57 if(IsEmpty(S)){ 58 printf("此栈为空,无法取栈头元素!\\n"); 59 exit(0); 60 }else{ 61 return S->Array[S->TopOfStack]; 62 } 63 } 64 //只删除头元素 65 void Pop(Stack S){ 66 if(IsEmpty(S)){ 67 printf("此栈为空,无法去除栈头元素!\\n"); 68 }else{ 69 S->TopOfStack--; 70 } 71 } 72 //获取头元素并删除 73 char *PopAndTop(Stack S){ 74 if(IsEmpty(S)){ 75 printf("此栈为空,无法执行获取栈头元素和去除栈头元素!\\n"); 76 exit(0); 77 }else{ 78 return S->Array[S->TopOfStack--]; 79 } 80 } 81 //释放栈空间 82 void DisposeStack(Stack s){ 83 if(s!=NULL){ 84 free(s); 85 } 86 } 87 void printStack(Stack s){ 88 int i; 89 for(i=0;i<=s->TopOfStack;i++){ 90 printf("%s ",s->Array[i]); 91 } 92 } 93 //位置是从栈头开始计算,所以谁小谁离栈顶比较远 94 int LastPosition(char *p,Stack temp){ 95 int i; 96 if(exist(p,temp)){ 97 for(i=temp->TopOfStack;i>=0;i--){ 98 if(strcmp(temp->Array[i],p)){ 99 return i; 100 } 101 } 102 } 103 else{ 104 printf("临时栈没有%s这个操作符\\n",p); 105 return -1; 106 } 107 } 108 int IsNumber(char p){ 109 if(p>=\'0\'&&p<=\'9\'){ 110 return 1; 111 }else 112 return 0; 113 } 114 //由于这里允许负数的存在,所以与之前的函数不同 115 int IsOperator(char *p){//这个函数是给turnInto函数使用的 116 //当长度不为1.肯定是数字,不是操作符 117 if(p[1]!=\'\\0\'){ 118 return 0; 119 } 120 //当长度为1,且不为从0到9的数时,才是操作符 121 if(IsNumber(p[0])){ 122 return 0; 123 }else 124 return 1; 125 } 126 int exist(char *p,Stack temp){ 127 int i; 128 for(i=0;i<=temp->TopOfStack;i++){ 129 if(strcmp(temp->Array[i],p)==0){ 130 return 1; 131 } 132 } 133 return 0; 134 } 135 //用这个递归提取函数明显比以前用的顺序处理要好得多 136 void handleString(char *s,Stack s_center){ 137 //printf("即将操作的字符串%s\\n",s); 138 int i=0; 139 int flag=-1;//当递归调用这个函数,上一个函数的flag会影响下一个函数的flag值,所以最好每次用时都初始化,而且函数段中每次用flag都最好先赋初值 140 char temp[5]; 141 if(s[0]==\'\\0\'){ 142 return; 143 } 144 if(s[i]==\'(\'&&s[i+1]==\'-\'){//处理类似1.(-34*76+21)-12或者2.(-43)+76这种形式的表达式字符串 145 flag=0; 146 temp[flag]=\'-\'; 147 i=i+2;//i指到-号后的第一个数字 148 while(IsNumber(s[i])){ 149 temp[++flag]=s[i]; 150 temp[flag+1]=\'\\0\'; 151 i++; 152 }//如果数字过后的符号不是右括号,类似1 153 if(s[i]!=\')\'){ 154 Push("(",s_center); 155 Push(temp,s_center); 156 s=s+i; 157 handleString(s,s_center); 158 }else{//等于右括号,类似2 159 Push(temp,s_center); 160 i++; 161 s=s+i; 162 handleString(s,s_center); 163 } 164 } 165 //如果字符串的开头是是数字,就将这一串数字压栈,并将数字后的第一个操作符压栈 166 else//else不能少,这里是为了在一次调用此函数时只能执行一次操作,他们是互斥关系 167 if(IsNumber(s[i])){ 168 flag=-1; 169 while(IsNumber(s[i])){ 170 temp[++flag]=s[i]; 171 temp[flag+1]=\'\\0\'; 172 i++; 173 } 174 Push(temp,s_center); 175 s=s+i; 176 handleString(s,s_center); 177 } 178 else 179 if(!IsNumber(s[0])) { 180 temp[0]=s[0]; 181 temp[1]=\'\\0\'; 182 Push(temp,s_center); 183 handleString(s+1,s_center); 184 } 185 } 186 int Max(int a,int b){ 187 return a>b?a:b; 188 } 189 void turnInto(Stack A,Stack B){ 190 Stack s_temp=CreateStack(15); 191 int i;int max;int leftbracketPosition; 192 for(i=0;i<=A->TopOfStack;i++){ 193 //printStack(s_temp);printf("\\n"); 194 //如果不是操作符,直接输出到后缀表达式 195 if(!IsOperator(A->Array[i])){ 196 strcpy(B->Array[++B->TopOfStack],A->Array[i]); 197 //printf("输出中存的有:%s\\n",A->Array[i]); 198 }else{ 199 char c=A->Array[i][0]; 200 //printf("\\n操作的字符是第%d个%c\\n",i+1,A->Array[i][0]); 201 switch(c){ 202 case \'(\':{ 203 Push(A->Array[i],s_temp); 204 break; 205 } 206 case \')\':{ 207 while(!strcmp( "(",Top(s_temp) )==0){ 208 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 209 } 210 Pop(s_temp); 211 break; 212 } 213 case \'+\': 214 case \'-\':{ 215 if(exist("(",s_temp)){//如果存在左括号,将左括号右侧全部运算符弹出 216 while(Top(s_temp)[0]!=\'(\'){ 217 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 218 } 219 Push(A->Array[i],s_temp); 220 }else{//如果不存在左括号,将栈中所有元素弹出 221 while(!IsEmpty(s_temp)){ 222 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 223 } 224 Push(A->Array[i],s_temp); 225 } 226 break; 227 } 228 case \'*\': 229 case \'/\':{ 230 if(IsEmpty(s_temp)){ 231 Push(A->Array[i],s_temp); 232 } 233 else{ 234 if(exist("(",s_temp)){ 235 leftbracketPosition=LastPosition("(",s_temp); 236 if(exist("/",s_temp)||exist("*",s_temp)){ 237 max=Max(LastPosition("/",s_temp),LastPosition("*",s_temp)); 238 if(max>leftbracketPosition){//表明符号在左括号右侧 239 while(Top(s_temp)[0]!=\'*\' || Top(s_temp)[0]!=\'/\'){ 240 strcpy( B->Array[++B->TopOfStack],PopAndTop(s_temp) ); 241 } 242 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 243 Push(A->Array[i],s_temp); 244 }else{//符号在左括号左侧 245 Push(A->Array[i],s_temp); 246 } 247 }else{//存在左括号,但既不存在乘号也不存在除号,判断此时有没有乘方号 248 //如果有乘方号,且乘方号在左括号右侧 249 if(exist("^",s_temp)&&(LastPosition("^",s_temp)>leftbracketPosition)){ 250 strcpy( B->Array[++B->TopOfStack],PopAndTop(s_temp) ); 251 Push(A->Array[i],s_temp); 252 }else{//不存在乘方号或者存在乘方号,但乘方号在左括号的左侧 253 Push(A->Array[i],s_temp); 254 } 255 } 256 }else{//不存在左括号时,只要临时栈中有乘号或除号就不可能再有乘方号 257 if(exist("*",s_temp)||exist("/",s_temp)){ 258 while(Top(s_temp)[0]!=\'*\'&&Top(s_temp)[0]!=\'/\'){ 259 strcpy( B->Array[++B->TopOfStack],PopAndTop(s_temp) ); 260 } 261 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 262 Push(A->Array[i],s_temp); 263 }else{//表示既没有左括号也没有乘号或除号,此时考虑栈中有没有乘方号 264 if(exist("^",s_temp)){//如果有乘方号,肯定在栈顶 265 strcpy( B->Array[++B->TopOfStack],PopAndTop(s_temp) ); 266 Push(A->Array[i],s_temp); 267 }else{ 268 Push(A->Array[i],s_temp); 269 } 270 }//不存在*或/的结束 271 }//不存在左括号的结束 272 } 273 break; 274 } 275 case \'^\':{ 276 if(IsEmpty(s_temp)){ 277 Push(A->Array[i],s_temp); 278 }else{ 279 //最高优先级,但临时栈中有可能还有乘方号,要把临时栈中与当前操作符有相同优先级的并在左括号的右边的符号弹出 280 if(!exist("^",s_temp)){ 281 strcpy(s_temp->Array[++s_temp->TopOfStack],A->Array[i]); 282 break; 283 }else{ 284 if(exist("(",s_temp)&& ( LastPosition("(",s_temp)<LastPosition("^",s_temp) ) ){ 285 while(Top(s_temp)[0]!=\'^\'){ 286 //printf("%s",Top(temp)); 287 strcpy( B->Array[++B->TopOfStack],PopAndTop(s_temp) ); 288 //printf("输出中存的有:%s\\n",A->Array[i]); 289 } 290 strcpy(B->Array[++B->TopOfStack],PopAndTop(s_temp)); 291 //printf("输出中存的有:%s\\n",B->Array[B->TopOfStack]); 292 Push(A->Array[i],s_temp); 293 //printStack(temp); 294 }else{//包以上是关于数据结构和算法分析(11)树的简介的主要内容,如果未能解决你的问题,请参考以下文章