现代软件工程 第一章 概论 第1题——邓琨

Posted 2020-08-08

题目要求：

第一步： 像阿超那样，花二十分钟写一个能自动生成小学四则运算题目的命令行 “软件”， 分别满足下面的各种需求。下面这些需求都可以用命令行参数的形式来指定：

 

a) 除了整数以外，还要支持真分数的四则运算。 （例如：  1/6 + 1/8 = 7/24）

 

b) 让程序能接受用户输入答案，并判定对错。 最后给出总共 对/错 的数量。

 

c) 逐步扩展功能和可以支持的表达式类型，最后希望能支持下面类型的题目 （最多 10 个运算符，括号的数量不限制）：
         25 - 3 * 4 - 2 / 2 + 89 = ？
         1/2 + 1/3 - 1/4 = ？ 
        （5 - 4 ） * （3 +28） =？

 

 d) 一次可以批量出 100 道以上的题目，保存在文本文件中， 并且保证题目不能重复，（1+2） 和 （2+1） 是重复的题目。 怎么保证题目不重复呢，请看详细题目要求

     和同学们比较一下各自程序的功能、性能、实现方法的异同等等。

     如何对一个表达式求值？ 参考资料： 

　　http://hczhcz.github.io/2014/02/27/shunting-yard-algorithm.html  

　　https://en.wikipedia.org/wiki/Shunting-yard_algorithm  

 

　鉴于该问题的难度与工作量，我将该问题拆分成3个小阶段进行实现：

1：复合四则运算的求值

2：随机生成复合四则运算

3：增加对真分数和假分数的支持

　　分析：1.对于复合四则运算的求值，可以根据堆栈的特性，利用算数符合的优先级比较，对复合四则运算求值，详细的算法过程将在下文进行介绍。

　　　　　2.随机生成复合四则运算是本题目的一个难点，在进行思考过后，我觉得可以采用多次随机过程，生成四则运算表达式。第一次，随机参与计算的数字个数，第二次，随机数字的数值，第三次，随机数字间的四则运算符，第四次，随机括号的添加。注意，由于可能存在除0运算，所以要对这种错误情况进行排除。由于第三次和第四次随机过程的特殊性，即使在第三步出现例如：3 / 0  + 1 的运算表达式，但是如果第四次随机过程在算式 0 + 1 外生成括号，造成 3 / （ 0 + 1 ）的结果，这种算式也是正确的。因此，不能保证在随机生成复合四则运算的过程中进行除0的判断。

　　　　　　对于这个问题，我的个人思路是：在生成每一个复合四则运算后，进行复合运算求值，并在算法每一次求值过程中就行判断，如果出现除0错误，就抛出异常，标记当前生成的四则运算式子非法，进行重新生成。虽然除0的情况很多，这样会浪费大量的时间进行判断，但是由于问题的时间复杂度和空间复杂度都非常小，可以忽略不计。

　　　　　3.在增加真分数和假分数运算时候，只需要对每一种四则运算进行一次条件判断，因此无较大的难度。

 

一、复合四则运算的求值

表达式求值的算法：

　　我采用的是“算符优先法”，在表达式中，优先级的顺序是：

　　1、括号的优先级最高，对括号内的各种运算符有：先乘除，后加减，同级运算从做至右

　　2、先括号内，后括号外，多层括号，由内向外。

　　操作数可以是常量、变量、常数。
　　运算符有算术运算符、关系运算符、逻辑运算符。
　　界符包括左右括号算式结束符。
　　运算符和界符统称为“算符”。

　　

在算符集中，在每一个运算步，相邻的算符c1 和c2之间的关系是如下三种情况（c1出现在c2之前）：
c1<c2,c1的优先级低于c2
c1=c2,c1的优先级等于c2
c1>c2,c1的优先级大于c2

下图描述的算符的优先级：

 

为实现算符优先算法，在这里用了两个工作栈。一个存放算符OPTR，另一个存放数据OPND。算法思想是：

（1）首先置数据栈为空栈，表达式起始符“＃”为算符栈的栈底元素
（2）自左向右扫描表达式，读到操作数进OPND栈，读到运算符，则和OPTR栈顶元素比较（栈顶元素为c1，读到的算符为c2);
　　若c1<c2,则c2进栈继续扫描后面表达式；
　　若c1＝c2,则（“＝”），即括号内运算结束，将c1出栈，并且c2放弃,继并在操作数栈扫描后面表达式；
　　若c1>c2,则将c1出栈，并在操作数栈取出两个元素a和b按c1做运算，运算结果进OPND.
　　重复直到表达式求值完毕。

 

例如：表达式3*(7-2),求值过程如下表：

步骤	OPTR栈	OPND栈	输入字符	主要操作
1	#		3*（7-2）#	PUSH(OPND,‘3‘)
2	#	3	*（7-2）#	PUSH(OPTR,‘*‘)
3	#*	3	（7-2）#	PUSH(OPTR,‘(‘)
4	#*(	3	7-2）#	PUSH(OPND,‘7‘)
5	#*(	3 7	-2）#	PUSH(OPTR,‘-‘)
6	#*(-	3 7	2）#	PUSH(OPND,‘2‘)
7	#*(	3 7 2	）#	operate（7-2）
8	#*(	3 5	）#	pop（）
9	#*	15	#	operate（3*5）
10	#	15	#	PUSH(OPTR,‘#‘)

 

为使两个算符比较方便,给算符设置优先级,如下表,其中c1为栈内元素,c2为栈外元素：

 

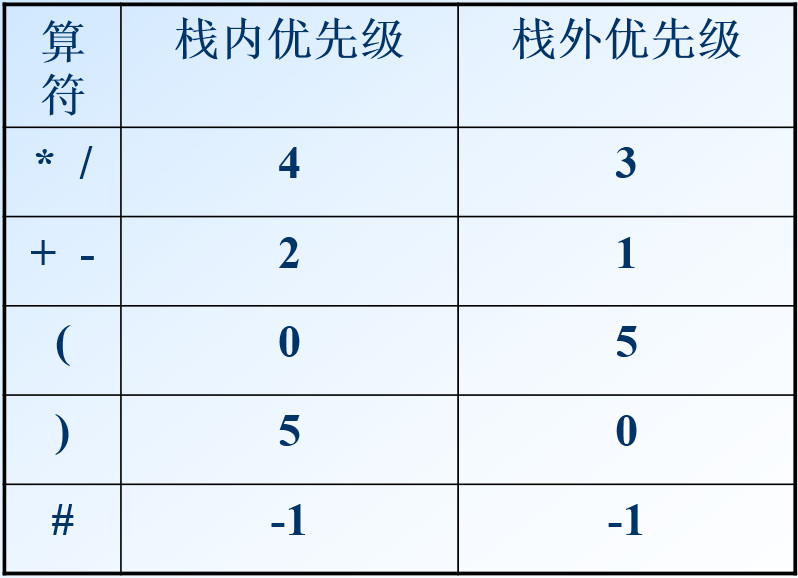
算符比较算法：　　

char Precede(char c1,char c2)
{int c_temp1,c_temp2;
switch(c1)
{ case ‘*’:
case ‘/’:c_temp1=4;break;
case ‘+’:
case ‘-’:c_temp1=2;break;
case ‘(’:c_temp1=0;break;
case ‘)’:c_temp1=5;break;
case ‘#’:c_temp1=-1;
}

 

switch(c2)
{ case ‘*’:
case ‘/’:c_temp2=3;break;
case ‘+’:
case ‘-’:c_temp2=1;break;
case ‘(’:c_temp2=5;break;
case ‘)’:c_temp2=0;break;
case ‘#’:c_temp2=-1;}
if(c_temp1<c_temp2) return(‘<‘);
if(c_temp1=c_temp2) return(‘=‘);
if(c_temp1>c_temp2) return(‘>‘);
}

 

int express()
{
Initstack(OPTR);Push(OPTR,’#’);
InitStack(OPND);
w=getchar();
while(w!=‘#’||GetTop(OPTR)!=‘#’)
   {if(!In(w,OP)){Push(OPND,w);w=getchar();}
else        //OP是操作符集合
switch(Precede(GetTop(OPTR),w))
{case ‘<‘:   Push(OPTR,w);w=getchar();break;
case ‘=‘:   Pop(OPTR);w=getchar();break;
case ‘>‘:   op=Pop(OPTR);b=Pop(OPND);a=Pop(OPND);
push(OPND,Operate(a,op,b));break;}}
return(Getop(OPND)
);

 

算符优先算法求表达式值：

OperandType EvaluateExpression() {
    InitStack (OPTR); Push ( OPTR,’#’);
    InitStack (OPND); c=getchar();
    while (c!=‘#’|| GetTop(OPTR)!=‘#’) {
        if(!In(c,OP)){Push(OPND,c);
            c=getchar();}
        else
            switch(Precede(GetTop(OPTR),c){
            case ‘<‘://栈顶元素优先权低
                Push(OPTR,c); c=getchar();
                break;
                        case ‘=‘://脱括号
                Pop(OPTR,x); c=getchar();
                break;
            case ‘>’://退栈并计算
                Pop(OPTR,theta);
                Pop(OPND,b); Pop(OPND,a);
                Push(OPND, Operate(a,theta,b));
                break;
            }//switch
    }//while
    return GetTop(OPND);
}//EvaluateExpression