NOIP训练规律+数论欧拉函数的应用
Posted Spana
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了NOIP训练规律+数论欧拉函数的应用相关的知识,希望对你有一定的参考价值。
Problem 1
【题目大意】
给出 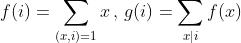
多组数据 ,给出
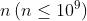 求出
求出 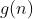 。
。
题解
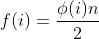
证明: 除了
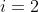 以为均为偶数, 所以互质的个数成对。
以为均为偶数, 所以互质的个数成对。
由 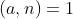 得
得 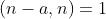 。
。
所以对于每对的和为 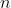 , 共有
, 共有 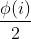 对 。
对 。
则 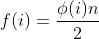
Problem 2
【题目大意】
在第一个圆上写入 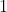 ,在第二个圆上写入
,在第二个圆上写入 ,此后每一次在前一个圆的基础上,每两个数之间写上他们的和,定义
,此后每一次在前一个圆的基础上,每两个数之间写上他们的和,定义 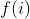 为第i个圆中数字i的个数。
为第i个圆中数字i的个数。
给出 ) ,求
,求 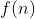 。
。
题解
)
证明: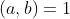 则
则 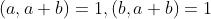 ,圆中的数字相邻两两互质。
,圆中的数字相邻两两互质。
对于一个数字  只可能由与他互质的两个数
只可能由与他互质的两个数 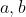 相加而成并且每一种构造方法是唯一的。
相加而成并且每一种构造方法是唯一的。
所以 ) 。
。
以上是关于NOIP训练规律+数论欧拉函数的应用的主要内容,如果未能解决你的问题,请参考以下文章