求和为0的最长连续子序列长度

Posted 2020-08-07 p_string

 

题意：给定一个数组，数组中元素的值只能是1或者-1，求其和为0的最长连续子序列的长度；

　　　　数组为1，-1，1，-1，1，-1，1，-1，其结果为：8

　　　　数组为1，1，-1，1，1，-1，-1，其结果为：6

解析：

　　通过分析可知，要使其和为0，只有当1和-1的个数相等时，才会成立，但题目要求是连续子序列，所以单纯统计其1和-1个数不可取。

　　由题目中求最长连续子序列，可想到动态规划来求解，动态规划的求解既是寻找其状态转移方程和建立状态转移表的过程

　　设dp[i]为下标为i及其之前数组中所有元素的和，

　　                                             

 

   
 

 

 

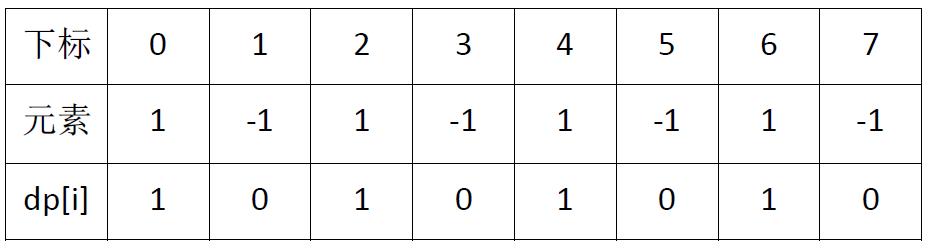
如图所示，数组为1，-1，1，-1，1，-1，1，-1最后一个值为0，直接满足结果，输出8

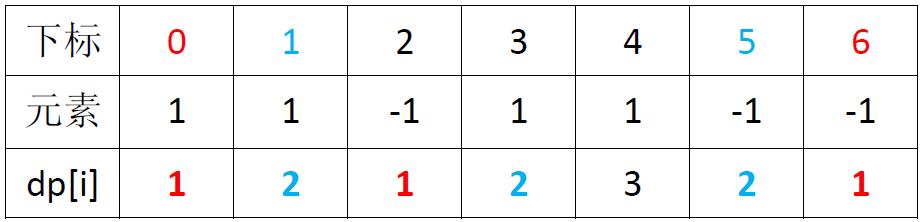
如上图，数组1，1，-1，1，1，-1，-1，dp取值为dp[0] = dp[2] = dp[6] = 1; dp[1] = dp[3] = d[5] = 3; dp[4] = 3;

对于每个值，取最后一次出现的位置和第一次出现的位置之差，取它们的最大值，max((6 - 0),(5 - 1),(4 - 4) = 6

代码如下所示：

 1 #include <cstdio>
 2 #include <map>
 3 #include <vector>
 4 #include <iostream>
 5 #include <cstdlib>
 6 
 7 using namespace std; 
 8 
 9 int main()
10 {
11     int n,val;
12     while (cin >> n) {
13         vector<int> arr(n + 1);
14         for (int i = 1; i <= n; i++) {
15             cin >> val;
16             arr[i] = val;
17         }
18         vector<int> dp(n + 1);
19         dp[1] = arr[1];
20         for (int i = 2; i <= n; i++)
21             dp[i] = arr[i] + dp[i - 1];
22 
23         //求取dp[i] = dp[j],i表示dp[i]的值第一次出现的位置，j表示其最后一次出现的位置
24         //for (const auto &s : dp)
25         //    cout << s << " ";
26         //cout << endl;
27         map<int, int> m;
28         int begin, max = 0;
29         for (int i = 1; i <= n; i++) {
30             begin = m[dp[i]];
31             if (begin == 0 && dp[i] != 0) {
32                 m[dp[i]] = i;
33             }
34             else {
35                 if (i - begin > max) {
36                     max = i - begin;
37                 }
38             }
39         }
40         cout << max << endl;
41     }
42     system("pause");
43     return 0;
44 }