MySTL: BM算法和Sunday快速字符串匹配算法

Posted 2020-06-13

　　BM算法研究了很久了，说实话BM算法的资料还是比较少的，之前找了个资料看了，还是觉得有点生涩难懂，找了篇更好的和算法更好的，总算是把BM算法搞懂了。

　　1977年，Robert S.Boyer和J Strother Moore提出了另一种在O(n)时间复杂度内，完成字符串匹配的算法，这个算法在单模匹配上比KMP算法还要出色

　　PS：其BM算法在跳转优化上的确比KMP算法要好很多，能在O(N)的上界就完成匹配了，但是不是绝对的，我们讲到后面再来说这个问题。

　　我们知道，KMP算法之所以能那么快，是因为他用了一种很巧妙的方法（也就是Next数组）完成了对前面匹配结果的记忆，使得我们不用重复扫描目标串，这是对串的前缀的一种非常极致的运用，BM算法也一样是这样想的。但是不同的地方在于，KMP算法是从模式串的开始往后匹配的，但是BM算法是从模式串结尾开始往前匹配的，BM算法利用了串的后缀的信息，用了两个类似于KMP的Next数组的表来储存模式串的信息，一个是坏字符表，一个是好后缀表，那么这两个表分别是怎么工作的呢？我们来一个一个看。

　　（另这篇文章我还是想引用一下别人的图吧，文字自己写，毕竟别人的图画的实在太好看了哈哈哈）

　　★坏字串表有两种情况

　　1.目标串中出现了模式串中没有的字符，此时模式串直接整体对齐到这个字符的后方，继续比较，如图：

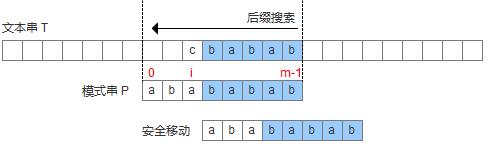
　　2.目标串中出现了A字符，而且不与其他字串形成后缀（这句话是我加的，其实这个情况也可以理解为好后缀表的len==1的特殊情况），则把模式串最右的那个A字符与目标串对齐。

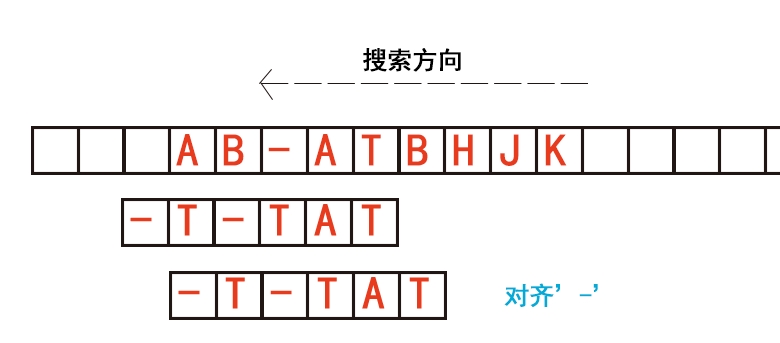
　　（原来的文章那个图是有错误的，自己做了一个新的）

　　★所以现在我们就可以来构建坏字符表了，这个还是比较简单的，按照上面的思路，假定我们只移动目标串（整个BM算法的精髓其实也就是移动目标串的方式上），那么如果按照第一种情况，那么我们只用移动p_len的单位就可以了(p_len指的是模式串(pattern)的长度)，如果坏字符出现在串中，那么我们必须移动m-(1+i)个单位了（i是指坏字符在pattern中的位置）。也就是我们只用初始化一遍坏字符表所有元素都是p_len，然后根据坏字符出现的位置规定移动的位置就好了！（Bad_List用的是散列的方法，散列ASCII的256个字符就可以了）。

　　先定义两个东西，Position是int，_String是char *

　　 1 typedef int Postion;2 typedef char * _String; 

　　代码：

1 void BuildBads(_String pattern, const int p_len, int *const BadS_List)
2 {
3     fill(BadS_List, BadS_List + 256, p_len);
4     for (int i = 0; i < p_len; i++)
5         BadS_List[pattern[i]] = p_len - 1 - i;
6 }

　　★现在就是好字符表的构造：

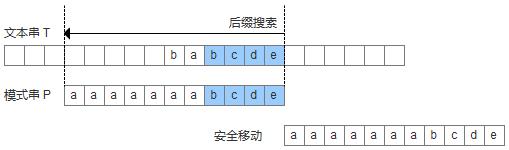
　　1.如果模式串中存在已经匹配成功的好后缀，则把目标串与好后缀对齐，然后从模式串的最尾元素开始往前匹配。如图：

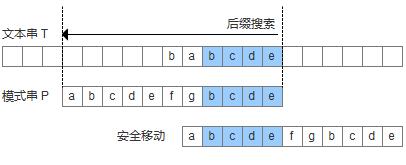
　　2.如果无法找到匹配好的后缀，那么我们就找一个匹配的最长的前缀，让目标串与最长的前缀对齐（如果这个前缀存在的话）。

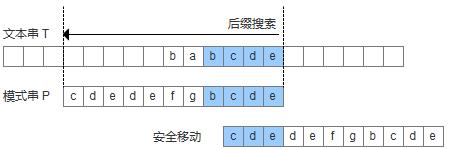
　　3.如果无法找到前缀，而且也没有好后缀，则直接让目标串的下一个p_len长度字符串与模式串进行匹配，如图：

　　★接下来就是怎么构建一个好字符串表的问题了，这里提供两个思路，

　　第一个是O(n^3)的算法的思路。

　　1.首先定义一个pre[i]数组，pre[i]数组的意思其实和KMP算法的最长公共长度表是差不多的，但是这个有点不一样，pre[i]储存的是从pattern[k]~pattern[k+p_len -1 -i]和pattern[i+1]~pattern[p_len - 1]相等，且pattern[k]!=pattern[i]的最大的k值（相当于后缀的匹配），在构建pre表的时候我们顺便把最大的前缀长度记录起来！我们可以把pre全部初始化为p_len，然后一个一个枚举就可以了，然后我们开始构建good_list，根据good_list的性质，我们可以得到：

　　1.如果pre[i]!=p_len，则说明是第一种情况，我们直接把目标串向前移动p_len-1-pre[i]个单位，

　　2.如果pre[i]==p_len，这里分两种情况，如果存在前缀，则我们把目标串直接与前缀对齐（但是前提是匹配的个数已经比前缀的长度要大），则移动p_len-1-i-c个单位（C就是前缀的长度）；如果不存在前缀，或者匹配的长度还不够前缀的长度，我们就直接移动p_len-1-i就可以了。

　　于是有下面这个很难懂的代码，注意我把pre[i]和good_list写一起了，因为pre只用一次，思路来源于参考1，算法时间复杂度O(n^3)（两个for加一个memcpy，原博主说自己的算法的复杂度是O(n^2)是不对的，明明memcpy那里还要算O(n)），另外注意这个算法Good_List最后一位固定是1

 1 void BuildGoods_Slow(_String pattern, const int p_len, int *const Goods_List)
 2 {
 3     //以O(n^3)的时间构建好后缀表
 4     int max_suffix_length = 0;
 5 
 6     fill(Goods_List, Goods_List + p_len, p_len);
 7     Goods_List[p_len - 1] = 1;//最后一位固定是1
 8 
 9     for (Postion i = p_len - 1; i > 0; i--)
10     {
11         if (Inffix_Suffix_Compare(pattern, pattern + i, p_len - i))
12             max_suffix_length = p_len - i;//记录最长的后缀
13         for (Postion j = 1; j < i; j++)
14         {
15             if (Inffix_Suffix_Compare(pattern + j, pattern + i, p_len - i)
16                 && pattern[i - 1] != pattern[j - 1])//一定要是不等于的时候才记录，最长后缀的最大k值
17                 Goods_List[i - 1] = j - 1;
18         }
19     }
20 
21     for (Postion i = 0; i < p_len; i++)
22     {
23         if (Goods_List[i] != p_len)
24             Goods_List[i] = p_len - (Goods_List[i] + 1);//下标是从0开始的,而且要对齐后缀
25         else//Goods_List[i]==p_len
26         {
27             Goods_List[i] += p_len - (1 + i);//下标是从0开始的
28             if (max_suffix_length != 0 && p_len - 1 - i >= max_suffix_length)
29                 Goods_List[i] -= max_suffix_length;
30         }
31     }
32 }
33 
34 bool Inffix_Suffix_Compare(_String sx, _String sy, const int len)
35 {
36     for (int i = 0; i < len; i++)
37         if (sx[i] != sy[i])
38             return false;
39     return true;
40 }

　　第二个是很巧妙的算法，算法时间复杂度O(n^2)

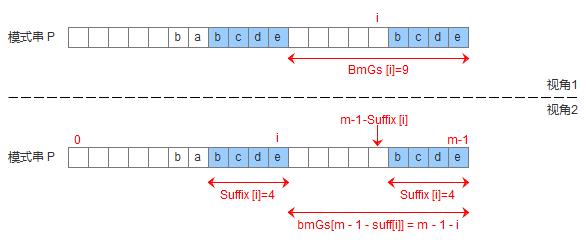
　　1.我们首先定义一个suff数组，这个数组和pre的定义是一样的，但是说法可能不太一样，suff[i]表示以i为边界，与模式串后缀匹配的最大长度，如图：

　　有了suff数组，我们直接定义Good_List数组，实现方式与第一种算法的类似：

　　1.模式串中有子串匹配上好后缀

　　2.模式串中没有子串匹配上好后缀，但找到一个最大前缀

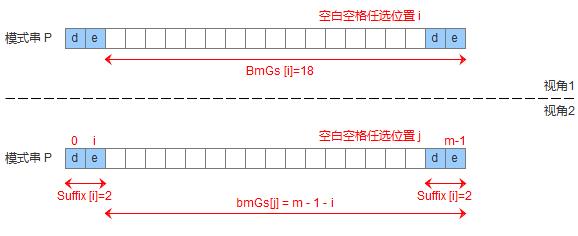
　　3.模式串中没有子串匹配上好后缀，但找不到一个最大前缀

　　先上代码：

 1 void BuildGoods_Fast(_String pattern, const int p_len, int *const Goods_List)
 2 {
 3     int *suff = new int[p_len];
 4     //构建suff表..................................................
 5     suff[p_len - 1] = p_len;
 6     for (Postion i = p_len - 2; i >= 0; i--)
 7     {
 8         Postion k = i;
 9         while (k >= 0 && pattern[k] == pattern[p_len - 1 - (i - k)])
10             k--;
11         suff[i] = i - k;//设定最长后缀的位置
12     }
13     //............................................................
14     fill(Goods_List, Goods_List + p_len, p_len);
15     for (Postion i = p_len - 1, j = 0; i >= 0; i--)
16         if (suff[i] == i + 1)
17             for (; j < p_len - (i + 1); j++)
18                 if (Goods_List[j] == p_len)
19                     Goods_List[j] = p_len - (j + 1);
20     //以上代码是符合Good_List的第三和第二规则，复杂度是O(n^2)
21     //不用排最后一个了，因为最后一个肯定是直接移动p_len的
22     for (Postion i = 0; i < p_len - 1; i++)
23         Goods_List[p_len - 1 - suff[i]] = p_len - (1 + i);
24         //Goods_List的值一直更新最小的，移动更小的位置达到更好的匹配效果
25     delete suff;
26 }

 　首先我们先来研究怎么构建suff数组，根据suff数组的定义，其实根据定义我们就知道，我们只用从后往前枚举pattern[i-k+1]~pattern[i]==pattern[p_len-1-k+1]~pattern[p_len-1]，从而suff[i]==k（也就是得到了i位置的最长后缀长度）这里的时间复杂度是O(n^2)，这就是代码的5-12行所做的事情。

    接下来我们要设定good_list，我们知道，如果我们要保证不漏掉任何一个匹配的可能，那么首先目标串的移动要尽可能地少（其实坏字符表的构建也是一样的），我们每次的操作都要保证移动goodlist的值一定要是所有的可能最小的。而我们再来看好后缀表移动的距离，我们发现移动的距离是情况1<=情况2<=情况3，而情况3相当于k=0的特殊情况，所以现在我们先来设定情况2和情况3。

    代码14行，也就是fill那一段，就是对情况3的实现，一旦情况3发生，我们直接让目标串移动p_len的距离重新匹配。时间复杂度O(n)。

    代码15-19行，这是一段时间复杂度为O(n)的代码（虽然有两个for，但是good_list的每个位置最多会被改变一次），而suff[i]==i+1也就证明pattern[0]~pattern[i]==pattern[p_len-1-i]~pattern[p_len-1]，也就是情况2的前缀情况，所以我们直接让这个移动p_len-1-j个位置对齐前缀。

    最后代码20-23，就是对情况1的实现而suff[i]对于不同的i有可能是一样的，但是我们想good_list最小，所以我们就把i从小往大枚举，最后的good_list就是最小的。这里的时间复杂度是O(n)。

    

    最后我们来实现BM的主算法，其实BM主算法和KMP的主算法的思想是差不多的，只是BM算法利用了坏字符表和好后缀表进行跳转。当某个字符匹配成功的时候，我们把目标串和模式串都往前移动一个位置继续匹配（因为匹配是从后往前匹配的），如果匹配失败，我们就把目标串失配的那个位置向后移动这个失配字符的在坏字符表和好后缀表中的最大的那个值。（为什么这里又不是最小了呢？因为我们坏字符表和好后缀表的位置都是已经保证了移动正确性为前提的了，现在我们想要算法更加的高效，那么目标串的移动肯定要尽量大一点的了。）

    代码：

 1 bool BmSearch(_String target, _String pattern)
 2 {
 3     int t_len = strlen(target), p_len = strlen(pattern);
 4     int *BadS_List = new int[256];
 5     int *Goods_List = new int[p_len];
 6 
 7     BuildBads(pattern, p_len, BadS_List);
 8     //BuildGoods_Slow(pattern, p_len, Goods_List);
 9     BuildGoods_Fast(pattern, p_len, Goods_List);
10 
11     Postion i = p_len - 1, j = p_len - 1;
12 
13     while (j < p_len)
14     {
15         while(j > 0 && target[i] == pattern[j])
16         {
17             i--;
18             j--;
19         }
20         if (j == 0 && target[i] == pattern[j])
21         {
22             delete BadS_List, Goods_List;;//找到一个就可以了
23             return true;
24         }
25         i += Goods_List[j] > BadS_List[target[i]] ? Goods_List[j] : BadS_List[target[i]];
26         j = p_len - 1;
27     }
28     delete BadS_List, Goods_List;
29     return false;
30 }

    至此我们已经完成了BM算法的全部内容，现在回到一开始我说的，为什么BM算法不是所有情况下都比KMP算法要快呢？BM算法的跳转确实比KMP算法要优秀，但是BM算法首先要构建一个好后缀表，这个表的构建是需要O(n^2)的复杂度的。如果目标串的规模很大（起码比模式串大O（n^2）个规模），那么BM算法才能在跳转上体现优势，这可能就是BM算法在算法竞赛上经常不被待见的原因吧。

    

　　最后我们来扯一下Sunday算法,它的思想跟BM算法很相似：

　　Sunday算法由Daniel M.Sunday在1990年提出，Sunday算法是从前往后匹配，在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符，如果该字符没有在模式串中出现则直接跳过，即移动位数 = 匹配串长度 + 1；否则，其移动位数 = 模式串中最右端的该字符到末尾的距离+1。

    其实Sunday算法就是用BM算法的坏字符表的实现的，只是Sunday算法是从前往后匹配，而且Sunday算法关注的是当前模式串在目标串的最后的位置的下一个位置的字符。举一个例子：

    

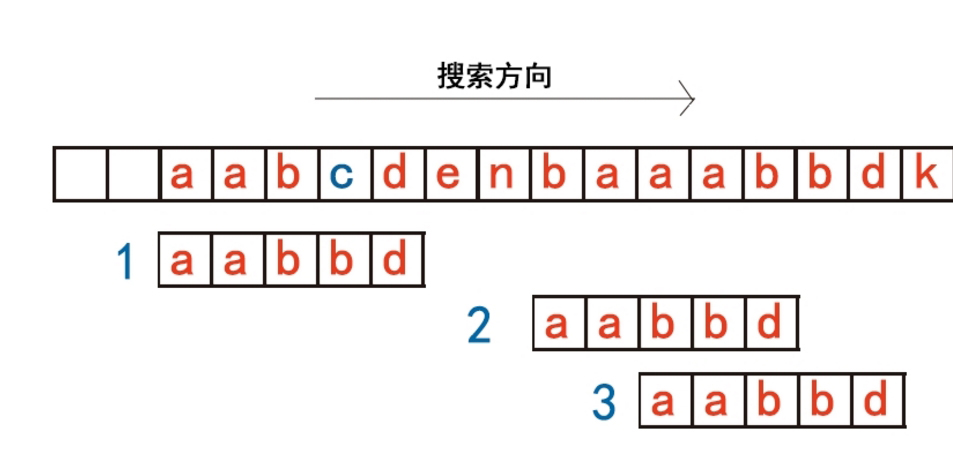
    上面的例子中，首先模式串与目标串匹配到如图的位置1，然后匹配到目标串的c失配，然后我们关注当前模式串在目标串的最后的位置的下一个位置的字符e，发现e并不在模式串中，再看n也不再模式串中，所以我们直接把模式串对齐到en的后面的位置2，继续匹配。

    但是第一个字符就失配了，我们关注当前模式串在目标串的最后的位置的下一个位置的字符b，b在模式串中，所以我们把这个b对齐到模式串中最右出现的b，完成匹配。

    Sunday算法获得比BM算法更大的跳跃距离，但是缺点很明显，就是很容易退化，比如在目标串baaabaaabaaaa寻找模式串aaaa，目标串最多只能跳两个位置，复杂度达到O(t_len*p_len)。

 

    总结：BM算法和KMP算法都很好地利用了前缀和后缀的匹配方式，都是很优秀的单模匹配算法，但是BM算法构建好后缀表需要花大量的时间，往往对于小规模匹配情况可能KMP算法和C标准函数strstr效果更好（毕竟strstr虽然是O(n^2)的算法，但是可能模式串也不是很大，而且这个函数可能是经过微软在汇编层进行过优化的。

 

　　参考1：http://blog.csdn.net/joylnwang/article/details/6785743
　　　　（略为复杂的一个讲述，说实话有些东西还是没讲的很清楚）
　　　　（这里的建表的复杂度其实是O(n^3)，是一个非常朴素的算法，原作者认为错了了，memcpy是一个一个比较的，他把这个函数调用过程看成O(1)了）
　　参考2：http://blog.csdn.net/v_july_v/article/details/7041827
　　　　　　BM算法和Sunday算法都讲的很简略，没有讲具体实现

　　参考3：http://www.cnblogs.com/xubenben/p/3359364.html
　　（原作者地址：http://www.searchtb.com/2011/07/%E5%AD%97%E7%AC%A6%E4%B8%B2%E5%8C%B9%E9%85%8D%E9%82%A3%E4%BA%9B%E4%BA%8B%EF%BC%88%E4%B8%80%EF%BC%89.html）
　　　（这个讲的比参考1思路清晰，而且算法比参考1优秀很多，建表是O(n^2)的算法，构造巧妙）
　　　　http://www-igm.univ-mlv.fr/~lecroq/string/node14.html 原C语言实现
　　　　http://www.cs.utexas.edu/users/moore/best-ideas/string-searching/fstrpos-example.html
　　　　http://www.cs.utexas.edu/users/moore/publications/fstrpos.pdf BM算法的原论文，有能力的而且想看算法分析的可以看看这里，里面的数学分析还是很值得参考的。

　　参考4：http://blog.csdn.net/sunnianzhong/article/details/8820123 Sunday算法