leetcode之374前K个高频元素Golang

Posted 2020-12-21

题目描述

给定一个非空的整数数组，返回其中出现频率前 *k* 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
• 你可以按任意顺序返回答案。

算法

本题的主要解题过程就是先用一个map保存数字和它出现次数的键值对，然后对这些键值对进行从大到小排序，选出前K个元素就可以了

所以本题的核心就是进行排序，我们在本题采用的排序方法是堆排序，也怪我，前面不知道go源码已经实现了堆排序的库，我们直接调用container/heap这个包就可以了，所以我先自己实现了堆排序，然后又用go语言内置的sort排序实现了一遍，最后采用go内置的堆排序又实现了一遍，所以本题我采用了三种解法

首先是我自己的堆排序

• 首先遍历map中的键值对，然后用这些键值对组成一棵完全二叉树
• 然后调整堆结构，让它成为一个大顶堆
  • ·采用层序遍历的方法
    • 比较当前子树根节点左右孩子结点的大小，保证根结点的值比孩子结点的值大，如果根结点的值小，就和孩子结点交换值
    • 层序遍历完成以后，如果上一次没有改变堆的结构，说明就已经是一个大顶堆了，否则再次层序遍历堆
• 重复下面这个过程
  • 取出堆的根结点
  • 然后将最后的结点位于根结点的位置，删除最后一个结点
  • 重新调整堆结构，保证是一个大顶堆
  • 如果没有取够k个值，就继续这个循环，然后再次获取

我的堆结构如下图所示：

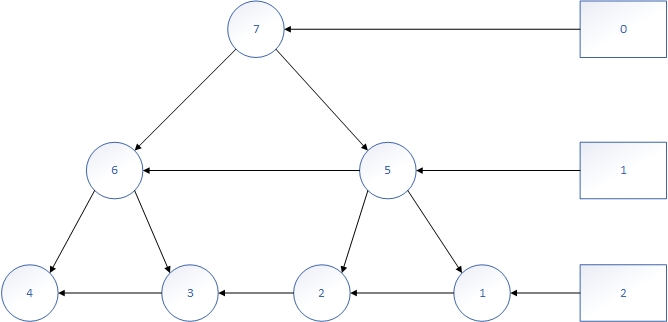
右边的矩形是一个数组，里面每一个元素是一个链表的头结点。链表的作用是用来定位最后一个结点的位置，例如当前最后一个结点是1，当我们将1移动到根结点并且删除原来结点1以后，新的最后一个结点就是2

代码

func topKFrequent2(nums []int, k int) []int {
	// 先用一个map来存储数字以及出现的次数
	numsMap := make(map[int]int)
	for _, num := range nums {
		numsMap[num]++
	}
	// 用这个map构建二叉树，用二叉树实现堆
	type node struct {
		num        int
		times      int
		leftChild  *node
		rightChild *node
		leftLoc    *node
		parent     *node
	}
	var root *node
	var topQue, downQue []*node
	var lOrR, newLine bool
	var parentNode *node
	var levelList []*node
	for key, value := range numsMap {
		tmpNode := &node{
			num:   key,
			times: value,
		}
		if root == nil {
			// 此时树还是空的
			root = tmpNode
			topQue = append(topQue, root)
			levelList = append(levelList, root)
		} else {
			// 此时树不是空的，从上层队列出队，下层队列入队
			if !newLine {
				// 这是新的一层
				levelList = append(levelList, tmpNode)
				newLine = !newLine
			} else {
				// 不是新的一层
				// 在每一层的链表头加上结点
				levelList[len(levelList)-1], tmpNode.leftLoc = tmpNode, levelList[len(levelList)-1]
			}
			if !lOrR {
				parentNode = topQue[0]
				topQue = topQue[1:]
				parentNode.leftChild = tmpNode
				parentNode.leftChild.parent = parentNode
				downQue = append(downQue, tmpNode)
			} else {
				parentNode.rightChild = tmpNode
				parentNode.rightChild.parent = parentNode
				downQue = append(downQue, tmpNode)
				if len(topQue) == 0 {
					topQue, downQue = downQue, topQue
					newLine = !newLine
				}
			}
			// downQue = append(downQue, tmpNode)
			lOrR = !lOrR
		}
	}
	// 然后将二叉树转化为大顶堆，按层序遍历
	topQue = []*node{root}
	var alterFlag bool
	for {
		if len(topQue) == 0 {
			if !alterFlag {
				break
			} else {
				topQue = []*node{root}
				alterFlag = false
			}
		}
		downQue = []*node{}
		for _, tmpNode := range topQue {
			if tmpNode.leftChild == nil && tmpNode.rightChild == nil {
				continue
			} else if tmpNode.leftChild != nil && tmpNode.rightChild != nil {
				// 既有左孩子又有右孩子
				downQue = append(downQue, tmpNode.leftChild, tmpNode.rightChild)
				var largerChild *node
				if tmpNode.leftChild.times >= tmpNode.rightChild.times {
					largerChild = tmpNode.leftChild
				} else {
					largerChild = tmpNode.rightChild
				}
				if tmpNode.times < largerChild.times {
					alterFlag = true
					tmpNode.num, tmpNode.times, largerChild.num, largerChild.times = largerChild.num, largerChild.times, tmpNode.num, tmpNode.times
				}
			} else {
				// 此时必定只有左孩子
				downQue = append(downQue, tmpNode.leftChild)
				if tmpNode.times < tmpNode.leftChild.times {
					alterFlag = true
					tmpNode.num, tmpNode.times, tmpNode.leftChild.num, tmpNode.leftChild.times = tmpNode.leftChild.num, tmpNode.leftChild.times, tmpNode.num, tmpNode.times
				}
			}
		}
		topQue = downQue
	}
	// 上面已经构造了一个大顶堆，每次只需要取出堆顶的数据就可以了，取k次
	var res []int
	for {
		res = append(res, root.num)
		k--
		if k == 0 {
			break
		}
		// 取完再调整堆
		lastNode := levelList[len(levelList)-1]
		root.num, root.times, lastNode.num, lastNode.times = lastNode.num, lastNode.times, root.num, root.times
		if levelList[len(levelList)-1] = lastNode.leftLoc; levelList[len(levelList)-1] == nil {
			levelList = levelList[:len(levelList)-1]
		}
		if lastNode.parent.rightChild != nil {
			lastNode.parent.rightChild = nil
		} else {
			lastNode.parent.leftChild = nil
		}
		// 再次调整堆
		tmpRoot := root
		for {
			if tmpRoot.leftChild == nil && tmpRoot.rightChild == nil {
				break
			} else if tmpRoot.leftChild != nil && tmpRoot.rightChild != nil {
				var largerChild *node
				if tmpRoot.leftChild.times >= tmpRoot.rightChild.times {
					largerChild = tmpRoot.leftChild
				} else {
					largerChild = tmpRoot.rightChild
				}
				if tmpRoot.times >= largerChild.times {
					break
				} else {
					tmpRoot.num, tmpRoot.times, largerChild.num, largerChild.times = largerChild.num, largerChild.times, tmpRoot.num, tmpRoot.times
					tmpRoot = largerChild
					continue
				}
			} else {
				// 只存在左孩子
				if tmpRoot.times >= tmpRoot.leftChild.times {
					break
				} else {
					tmpRoot.num, tmpRoot.times, tmpRoot.leftChild.num, tmpRoot.leftChild.times = tmpRoot.leftChild.num, tmpRoot.leftChild.times, tmpRoot.num, tmpRoot.times
					tmpRoot = tmpRoot.leftChild
					continue
				}
			}
		}
	}
	return res
}

第二个算法

首先同样使用map保存键值对，然后对这些键值对进行排序，使用官方的sort需要实现sort.Interface这个接口

type Interface interface {
    // Len方法返回集合中的元素个数
    Len() int
    // Less方法报告索引i的元素是否比索引j的元素小
    Less(i, j int) bool
    // Swap方法交换索引i和j的两个元素
    Swap(i, j int)
}

代码如下

type numMapToTimes struct {
	num   int
	times int
}

type mapSlice []*numMapToTimes
func (m mapSlice) Len() int {
	return len(m)
}
func (m mapSlice) Less(i, j int) bool {
	if m[i].times >= m[j].times {
		return true
	}
	return false
}
func (m mapSlice) Swap(i, j int) {
	m[i].num, m[i].times, m[j].num, m[j].times = m[j].num, m[j].times, m[i].num, m[i].times
}
func topKFrequent1(nums []int, k int) []int {
	var res []int
	numsMap := make(map[int]int)
	for _, num := range nums {
		numsMap[num]++
	}
	var slice mapSlice
	for key, v := range numsMap {
		tmpMap := &numMapToTimes{
			num:   key,
			times: v,
		}
		slice = append(slice, tmpMap)
	}
	sort.Sort(slice)
	for i := 0; i < k; i++ {
		res = append(res, slice[i].num)
	}
	return res
}

第三个算法就是采用官方的堆排序

需要实现的接口container/heap.Interface:

type Interface interface {
    sort.Interface
    Push(x interface{}) // 向末尾添加元素
    Pop() interface{}   // 从末尾删除元素
}

代码：

type numMapToTimes struct {
	num   int
	times int
}

type mapSlice []*numMapToTimes
// 当实现sort.Interface的时候，要用值实现哦
func (m mapSlice) Len() int {
	return len(m)
}
func (m mapSlice) Less(i, j int) bool {
	if m[i].times >= m[j].times {
		return true
	}
	return false
}
func (m mapSlice) Swap(i, j int) {
	m[i].num, m[i].times, m[j].num, m[j].times = m[j].num, m[j].times, m[i].num, m[i].times
}

func (m *mapSlice) Push(x interface{}) {
	// 向末尾添加元素
	// item:=x.(*mapSlice)
	// *m = append(*m,*item...)
	// 因为这个方法是指针实现的，所以当调用指针指向的值的时候，需要在前面加*
	// 类似于x.(type)这种只有当x的类型是interface{}的时候使用，并且它的作用是检查类型是否匹配
	// 因为一个接口类型中包含了值域和类型域
	// x.(int)就是检查类型域是不是int，x.(*numMapToTimes)检查类型域是不是numMapToTimes指针
	*m = append(*m, x.(*numMapToTimes))
}

func (m *mapSlice) Pop() interface{} {
	// 从末尾删除元素
	// 这个方法还是指针实现的，所以前面加*，并且根据优先级，*m需要括起来
	res := (*m)[len(*m)-1]
	*m = (*m)[:len(*m)-1]
	return res
}

func topKFrequent(nums []int, k int) []int {
	res := make([]int, 0)
	numsMap := make(map[int]int)
	for _, num := range nums {
		numsMap[num]++
	}
	slice := &mapSlice{}
	// 用实现了heap.Interface接口的类型来初始化堆
	heap.Init(slice)
	for key, value := range numsMap {
		tmpMap := &numMapToTimes{key, value}
		// 向堆中加入数据
		heap.Push(slice, tmpMap)
	}
	for i := 0; i < k; i++ {
		// 从堆中弹出数据
		elem := heap.Pop(slice)
		res = append(res, elem.(*numMapToTimes).num)
	}
	return res
}