学数答题160903-三角函数

Posted 2020-08-06

题160903设$\\alpha ,\\beta $均为锐角，满足

${{\\sin }^{2}}\\alpha +{{\\sin }^{2}}\\beta =\\sin (\\alpha +\\beta )$，

求$\\alpha +\\beta $的值．

---

 试题来源：2016年北大全国优秀中学生暑期学堂

解：显然当$\\alpha +\\beta =\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}$时，等式成立；

由已知条件知${{\\sin }^{2}}\\alpha +{{\\sin }^{2}}\\beta =\\sin \\alpha \\cos \\beta +\\cos \\alpha \\sin \\beta $，

整理得$\\sin \\alpha (\\sin \\alpha -\\cos \\beta )=\\sin \\beta (\\cos \\alpha -\\sin \\beta )$．

若$\\alpha +\\beta \\ne \\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}$，则有$\\sin \\alpha -\\cos \\beta $与$\\cos \\alpha -\\sin \\beta $同号．

若它们同为正，则有$\\sin \\alpha >\\cos \\beta =\\sin \\left( \\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\beta  \\right)$，$\\cos \\alpha =\\sin \\left( \\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\alpha  \\right)>\\sin \\beta $，

从而有$\\alpha >\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\beta $，$\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\alpha >\\beta $，无解；

若它们同为负，用类似的方式也可以推导出矛盾．

综上，$\\alpha +\\beta =\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}$．

---

法2：由${{\\sin }^{2}}\\alpha +{{\\sin }^{2}}\\beta =\\sin (\\alpha +\\beta )$，$\\sin \\left( \\alpha +\\beta  \\right)\\le 1$，得${{\\sin }^{2}}\\alpha \\le 1-{{\\sin }^{2}}\\beta ={{\\cos }^{2}}\\beta $，

因为$\\alpha ,\\beta $均为锐角，所以$\\sin \\alpha \\le \\cos \\beta $，同理$\\sin \\beta \\le \\cos \\alpha $，

故$\\sin \\left( \\alpha +\\beta  \\right)=\\sin \\alpha \\cos \\beta +\\cos \\alpha \\sin \\beta $$\\ge {{\\sin }^{2}}\\alpha +{{\\sin }^{2}}\\beta $，

当且仅当$\\sin \\alpha =\\cos \\beta =\\sin \\left( \\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\beta  \\right)$，$\\sin \\beta =\\cos \\alpha =\\sin \\left( \\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\alpha  \\right)$时取等，

因为$\\alpha ,\\beta ,\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\alpha ,\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}-\\beta $均为锐角，所以$\\alpha +\\beta =\\dfrac{\\text{ }\\!\\!\\pi\\!\\!\\text{ }}{2}$．

---

学生解答

BAM提供：完全正确

 

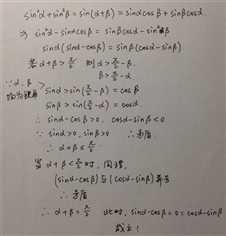
LST提供：完全正确

 

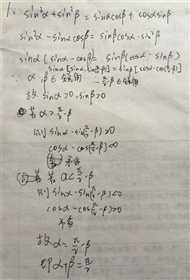
WQY提供：完全正确

 

FXY提供：完全正确

 

MJX提供：完全正确，解法巧妙

 

LZX提供：倒数2,3行错误