UVa221

Posted 2020-08-06 Yan_Bin

221 Urban Elevations
An elevation of a collection of buildings is an orthogonal projection of the buildings onto a vertical
plane. An external elevation of a city would show the skyline and the faces of the “visible” buildings of
the city as viewed from outside the city from a certain direction. A southern elevation shows no sides;
it shows the perfectly rectangular faces of buildings or parts of faces of buildings not obstructed on the
south by taller buildings. For this problem, you must write a program that determines which buildings
of a city are visible in a southern elevation.
For simplicity, assume all the buildings for the elevation are perfect rectangular solids, each with
two sides that run directly east-west and two running directly north-south. Your program will find the
buildings that appear in a southern elevation based on knowing the positions and heights of each city
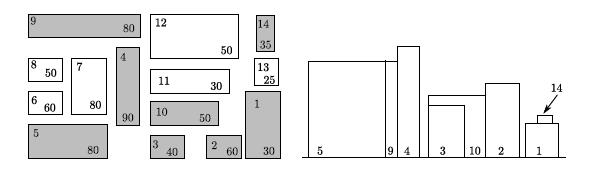
building. That data can be illustrated by a map of the city as in the diagram on the left below. The
southern elevation for that city is illustrated in the diagram on the right.
City map. Boldface numbers (in the upper left
of each building) identify the buildings. Plain
numbers (lower right) are the buildings heights.
Southern Elevation
(Only the shaded buildings are visible in a southern
elevation)
Input
Input for your program consists of the numeric description of maps of several cities. The first line of
each map contains the number of buildings in the city (a non-negative integer less than 101). Each
subsequent line of a map contains data for a single building — 5 real numbers separated by spaces in
the following order:
x-coordinate of the southwest corner
y-coordinate of the southwest corner
width of the building (length of the south side)
depth of the building (length of the west side)
height of the building
Each map is oriented on a rectangular coordinate system so that the positive x-axis points east and
the positive y-axis points north. Assume that all input for each map corresponds to a legitimate map
(the number of buildings is the same as the number of subsequent lines of input for the map; no two
buildings in a single map overlap). Input is terminated by the number 0 representing a map with no
buildings.
Universidad de Valladolid OJ: 221 – Urban Elevations 2/2
Output
Buildings are numbered according to where their data lines appear in the map’s input data — building
#1 corresponding to the first line of building data, building #2 data to the next line, and building
#n to the nth line of building data for that map. (Buildings on subsequent maps also begin their
numbering with 1.)
For each map, output begins with line identifying the map (map #1, map #2, etc.) On the next line
the numbers of the visible buildings as they appear in the southern elevation, ordered south-to-north,
west-to-east. This means that if building n and building m are visible buildings and if the southwest
corner of building n is west of the southwest corner of building m, then number n is printed before
number m. If building n and building m have the same x-coordinate for their southwest corners and if
building n is south of building m, then the number n is printed before the number m.
For this program, a building is considered visible whenever the part of its southern face that appears
in the elevation has strictly positive area. One blank line must separate output from consecutive input
records.
Sample Input
14
160 0 30 60 30
125 0 32 28 60
95 0 27 28 40
70 35 19 55 90
0 0 60 35 80
0 40 29 20 60
35 40 25 45 80
0 67 25 20 50
0 92 90 20 80
95 38 55 12 50
95 60 60 13 30
95 80 45 25 50
165 65 15 15 25
165 85 10 15 35
0
Sample Output
For map #1, the visible buildings are numbered as follows:
5 9 4 3 10 2 1 14

题意：

       有n个建筑物，输入每个建筑物的左下角（俯视图）坐标（即x、y坐标的最小值）、宽度（即x方向的长度）、深度（即y方向的长度）和高度（以上均为实数），输出正视图中能看到的所有建筑物，按照左下角x坐标从小到大进行排序，左下角x坐标相同时按照y坐标从小到大排序。这道题的输入不会引起精度问题。

分析：

       显然，我们可以忽略所有建筑物“深度”这一属性。将建筑物按输出顺序进行排序后一次进行判断是否在正视图中可见。

       由于x坐标上在实数范围内有无限个点，不可能枚举所有的坐标，所以我们的办法就是离散化。将所有的建筑物的左右点坐标存储与数组x中，然后对x进行排序去重，则数组中任意两个相邻x坐标形成的区间要么完全可见，要么完全不可见。这样，只需要在该区间任意选取一点（我们选取中点），就能判断某一个建筑物在该区间内是否可见。

       如果建筑物的坐标中包含某个x坐标并且建筑物的南面不存在另外的不比它矮的建筑物也包含这个x坐标则该建筑物在这个x坐标处可见。

 1 #include <cstdio>
 2 #include <algorithm>
 3 using namespace std;
 4 const int maxn = 100;
 5 struct Building{
 6     int id;
 7     double x,y,w,d,h; // 左下角坐标、x方向宽、y方向宽、高度
 8     bool operator <(const Building& rhs)const{
 9         return x < rhs.x || (x == rhs.x && y < rhs.y);
10     }
11 }b[maxn + 1];
12 int n;
13 double x[maxn * 2 + 1]; // 存储所有的x坐标
14 // 判断在x坐标上mx处向北看视线是否穿过（不考虑遮挡）建筑i
15 bool cover(int i,double mx){
16     return b[i].x <= mx && b[i].x + b[i].w >= mx;
17 }
18 // 判断建筑物i在x=mx处是否可见
19 bool visible(int i,double mx){
20     if(!cover(i,mx)) return false;
21     for(int k = 0 ; k < n ; k++)
22     // 如果有一座更高的建筑物在南面挡住了视线
23     if(b[k].y < b[i].y && b[k].h >= b[i].h && cover(k,mx)) 
24         return false;
25     return true;
26 }
27 int main(){
28     int kase = 0;
29     while(scanf("%d",&n) == 1 && n){
30         for(int i = 0 ; i < n ; i++){
31             scanf("%lf%lf%lf%lf%lf",&b[i].x,&b[i].y,&b[i].w,&b[i].d,&b[i].h);
32             x[2 * i] = b[i].x,x[2 * i + 1] = b[i].x + b[i].w;
33             b[i].id = i + 1;
34         }
35         sort(b,b + n); // 按题目要求排序建筑物方便输出
36         sort(x,x + 2 * n); // 所有的x坐标进行排序
37         int m = unique(x,x + n * 2) - x; // 排序后去重，得到m个坐标
38         if(kase++) printf("\\n");
39         printf("For map #%d, the visible buildings are numbered as follows:\\n%d",kase,b[0].id);
40         for(int i = 1 ; i < n ; i++){ //判断剩下的n-1个建筑的可见情况
41             bool vis = false;
42             for(int j = 0 ; j < m - 1 ; j++)
43             if(visible(i,(x[j] + x[j + 1]) / 2)){
44                 vis = true;
45                 break;
46             }
47             if(vis) printf(" %d",b[i].id);
48         }
49         printf("\\n");
50     }
51     return 0;
52 }

View Code