C语言实现压缩二例
Posted bcbobo21cn
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C语言实现压缩二例相关的知识,希望对你有一定的参考价值。
一 简单字符串压缩
编写一个字符串压缩程序,将字符串中连续出席的重复字母进行压缩,并输出压缩后的字符串。
压缩规则:
1、仅压缩连续重复出现的字符。比如字符串”abcbc”由于无连续重复字符,压缩后的字符串还是”abcbc”。
2、压缩字段的格式为”字符重复的次数+字符”。例如:字符串”xxxyyyyyyz”压缩后就成为”3x6yz”。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int main()
{
char str[100] = {'\\0'};
char res[100] = {'\\0'};
scanf("%s",str);
int length = strlen(str);
int i=0, j=0, k=0;
int count = 0;
do
{
if(i < length && str[i++] == str[j])
count++;
if(str[i] != str[j])
{
if(count <= 1)
res[k++] = str[j];
else
{
if(count > 1)
{
char temp[10] = {'\\0'};
itoa(count,temp,10);
strcpy(res+k,temp);
k+=strlen(temp);
res[k++] = str[j];
}
}
j = i;
count = 0;
}
}while(i<length);
res[k] = '\\0';
printf("The result is : %s\\n",res);
return 0;
}
运行情况:
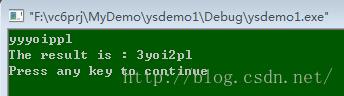
二 哈夫曼编码
哈夫曼树─即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。 在计算机信息处理中,
“哈夫曼编码”是一种一致性编码法(又称“熵编码法”),用于数据的无损耗压缩。这一术语是指使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。这种方法是由David.A.Huffman发展起来的。 例如,在英文中,e的出现概率很高,而z的出现概率则最低。当利用哈夫曼编码对一篇英文进行压缩时,e极有可能用一个位
哈弗曼编码在信息论中应用举例哈弗曼编码在信息论中应用举例
(bit)来表示,而z则可能花去25个位(不是26)。用普通的表示方法时,每个英文字母均占用一个字节(byte),即8个位。二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。若能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
//用C语言实现Huffman编码,并计算本节中块的编码
//长度(以位为单位),计算Huffman编码的压缩比。
//主程序:
#include<stdio.h>
#include<stdlib.h>
typedef struct HfTreeNode
{
int weight; //权重
int parent; //父节点
int lchild, rchild; //两个子节点
}Struct, *HfStruct;
typedef struct{
char code[10];
int start;
}HCodeType;
void quanDCT(short(*data)[8], short(*result)[8]);//量化函数
int calWeight(short(*result), int(*Node), int(*Weight));//权重计算
void print_data_screen(short data[8][8]);//数据打印
//待编码数据
short DctData[8][8] = {
{ 1149, 38, -43, -10, 25, -83, 10, 40 },
{ -81, -3, 114, -73, -6, -2, 21, -5 },
{ 13, -11, 0, -42, 25, -3, 16, -38 },
{ 1, -61, -13, -12, 35, -23, -18, 4 },
{ 43, 12, 36, -4, 9, -21, 6, -8 },
{ 35, -11, -9, -4, 19, -28, -21, 13 },
{ -19, -7, 20, -6, 2, 2, 11, -21 },
{ -5, -13, -11, -17, -4, -1, 6, -4 } };
HfStruct create_HuffmanTree(int *WeightPoint, int n);//霍夫曼树创建函数
void HuffmanCoding(HfStruct HT, HCodeType HuffCode[], int n);//霍夫曼编码函数
void main()
{
int i, j;//循环变量
int Length;//编码节点数
int totalbits = 0;//计算编码后的总的比特数
int Node[64];//节点数组
int Weight[64];//权重数组
short QuanResult[8][8];//量化结果存储
quanDCT(DctData, QuanResult);//数据量化
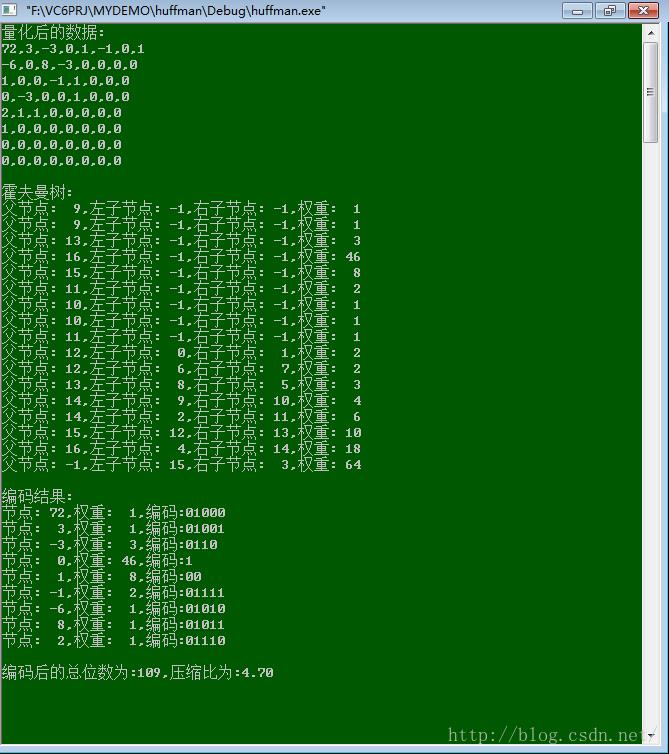
printf("量化后的数据:\\n");//打印量化数据
print_data_screen(QuanResult);
Length = calWeight(*QuanResult, Node, Weight);//计算量化数据的节点与权重,并返回节点数
int *maNode = (int*)malloc(Length*sizeof(int));//按有效节点进行分配
int *maWeight = (int*)malloc(Length*sizeof(int));//按有效节点进行分配
for (i = 0; i<Length; i++)
{
*(maNode + i) = Node[i];//拷贝有效节点
*(maWeight + i) = Weight[i];//拷贝有效权重
}
//根据权重与有效节点数创建霍夫曼树
HfStruct p = create_HuffmanTree(maWeight, Length);
//打印霍夫曼树
printf("霍夫曼树:\\n");
for (i = 0; i<2 * Length - 1; i++)
printf("父节点:%3d,左子节点:%3d,右子节点:%3d,权重:%3d\\n", p[i].parent, p[i].lchild, p[i].rchild, p[i].weight);
HCodeType code[9];
//依据霍夫曼树进行编码
HuffmanCoding(p, code, Length);//霍夫曼编码
//打印出编码结果
printf("\\n编码结果:\\n");
for (i = 0; i<Length; i++)
{
printf("节点:%3d,权重:%3d,编码:", *(maNode + i), *(maWeight + i));
for (j = code[i].start + 1; j < Length; j++)
printf("%c", code[i].code[j]);
printf("\\n");
}
//计算编码后的总的比特数,计算压缩比
for (i = 0; i<Length; i++)
{
j = Length - 1 - code[i].start;
totalbits = totalbits + maWeight[i] * j;
}
printf("\\n编码后的总位数为:%d,压缩比为:%4.2f\\n", totalbits, (double)(64 * 8) / totalbits);
while (1);
}
short QuanTable[8][8] = {
{ 16, 11, 10, 16, 24, 40, 51, 61 },
{ 12, 12, 14, 19, 26, 58, 60, 55 },
{ 14, 13, 16, 24, 40, 57, 69, 56 },
{ 14, 17, 22, 29, 51, 87, 80, 62 },
{ 18, 22, 37, 56, 68, 109, 103, 77 },
{ 24, 35, 55, 64, 81, 104, 113, 92 },
{ 49, 64, 78, 87, 103, 121, 120, 101 },
{ 72, 92, 95, 98, 112, 100, 103, 99 }
};//量化表
void print_data_screen(short data[8][8])//数据打印
{
int x, y;
for (x = 0; x<8; x++)
for (y = 0; y<8; y++)
{
printf("%d", data[x][y]);
if (y == 7)
{
if (x == 7)
printf("\\n\\n");
else
printf("\\n");
}
else
{
printf(",");
}
}
}
void quanDCT(short(*data)[8], short(*result)[8])//数据量化
{
int x, y;
for (x = 0; x<8; x++)
{
for (y = 0; y<8; y++)
{
*(*(result + x) + y) = (short)(double(*(*(data + x) + y)) / QuanTable[x][y] + 0.5);
}
}
}
int calWeight(short(*result), int *Node, int *Weigh)//计算权重
{
int x, y, i, find = 0;
for (x = 0; x<64; x++)
{
Node[x] = 0;
Weigh[x] = 0;
}
Node[0] = (*result);
Weigh[0] = 1;
i = 0;
for (x = 1; x<64; x++)
{
for (y = 0; y <= i; y++)
{
if (*(x + result) == Node[y])
{
Weigh[y]++;
find = 1;
break;
}
}
if (find)
{
find = 0;
continue;
}
else
{
i++;
Node[y] = *(x + result);
Weigh[y]++;
}
}
return i + 1;
}
/*
从HtStruct选出权重最小,并且没有父节点的节点
*/
int WeightMinNode(HfStruct HtStruct, int Mum)
{
int i = 0; //序号, 循环用
int min; //最小权重序号
int MinWeight; //最小权重
//首先选择一个节点,用于比较出最小的一个
while (HtStruct[i].parent != -1)
i++;
MinWeight = HtStruct[i].weight;
min = i;
//选出weight最小且parent为-1的元素,并将其序号赋给min
for (; i<Mum; i++)
{
if (HtStruct[i].weight<MinWeight&&HtStruct[i].parent == -1)
{
MinWeight = HtStruct[i].weight;
min = i;
}
}
//选出weight最小的元素后,将其parent置1,使得下一次比较时将其排除在外。
HtStruct[min].parent = 1;
return min;
}
/*
从HtStruct数组的前k个元素中选出weight最小且parent为-1的两个,分别将其序号保存在min1和min2中
*/
void ChoseMinium2(HfStruct HtStruct, int Mum, int *min1, int *min2)
{
*min1 = WeightMinNode(HtStruct, Mum);
*min2 = WeightMinNode(HtStruct, Mum);
}
/*
根据给定的n个权值构造一棵赫夫曼树
*/
HfStruct create_HuffmanTree(int *WeightPoint, int n)
{
//一棵有n个叶子节点的赫夫曼树共有2n-1个节点
int AllNodeNum = 2 * n - 1;
HfStruct HT = (HfStruct)malloc(AllNodeNum*sizeof(Struct));
int i;
//叶子节点初始化,将传入的数据加载到叶子节点上
for (i = 0; i<n; i++)
{
HT[i].parent = -1;
HT[i].lchild = -1;
HT[i].rchild = -1;
HT[i].weight = *WeightPoint;
WeightPoint++;
}
//HT[n],HT[n+1]...HT[2n-2]中存放的是中间构造出的每棵二叉树的根节点
for (; i<AllNodeNum; i++)
{
HT[i].parent = -1; //父节点初始化
HT[i].lchild = -1; //左子节点初始化
HT[i].rchild = -1; //右子节点初始化
HT[i].weight = 0; //权重初始化
}
int min1, min2;
int *ad_min1 = &min1;//用于传递最小权重的节点
int *ad_min2 = &min2; //用于传递最小权重的节点
//每一轮比较后选择出min1和min2构成一课二叉树,最后构成一棵赫夫曼树
for (i = n; i<AllNodeNum; i++)
{
ChoseMinium2(HT, i, ad_min1, ad_min2); //选出权重最小的两个节点
HT[min1].parent = i; //父节点赋值
HT[min2].parent = i; //父节点赋值
HT[i].lchild = min1; //左子节点赋值
HT[i].rchild = min2; //右子节点赋值
HT[i].weight = HT[min1].weight + HT[min2].weight; //权重为两个子节点权重之和
}
return HT;
}
/*
从叶子节点到根节点逆向求赫夫曼树HT中n个叶子节点的赫夫曼编码,并保存在code中
*/
void HuffmanCoding(HfStruct HT, HCodeType HuffCode[], int n)
{
HCodeType cd;
int i,j,current,father;
for (i = 0; i<n; i++)
{
cd.start = n - 1;
current = i; //定义当前访问的节点
father = HT[i].parent; //当前节点的父节点
//从叶子节点向上搜索
while (father != -1)
{
if (HT[father].lchild == current) //如果是左子节点,则编码为0
cd.code[cd.start--] = '0';
else//如果是右子节点,则编码为1
cd.code[cd.start--] = '1';
current = father;
father = HT[father].parent;
}
for (j = cd.start + 1; j <n; j++)
HuffCode[i].code[j] = cd.code[j];
HuffCode[i].start = cd.start;
}
}
以上是关于C语言实现压缩二例的主要内容,如果未能解决你的问题,请参考以下文章