MachineLearning：感知器perception算法

Posted 2020-08-04 coding如逆水行舟

简介

50年代末 F.Rosenblatt提出感知器算法。线性分类器的设计就是利用训练样本来计算线性函数的权向量

问题

设有两类问题的判别函数
　　　　　　　　$g(X)=w_1x_1+w_2x_2+w_3=0$
训练样本XA,XB∈ω1, XC,XD∈ω2则
　　　　　　　　　　 $g(XA)>0, g(XB)>0$
　　　　　　　　　　 $g(XC)<0 ,g(XD)<0$

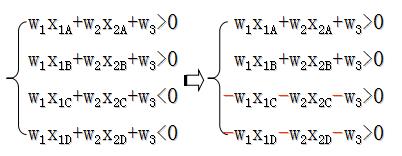
即：
　　　　　　　　　　 $W X > 0$
其中：
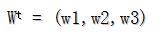　　　权向量
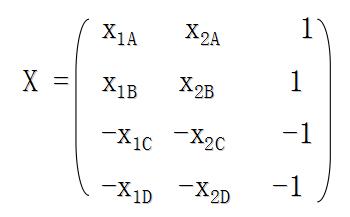　　　各样本特征向量的增1矩阵
该线性联立不等式只对线性可分问题有解，且是多解，因而只有按不同条件取最优解

 赏-罚训练算法是一个迭代过程：
  　　  1）取权向量W(1)为任一初始值；
    　　2）用训练集X对W进行迭代，在第k步
    　　3）如Xk∈ ω1 且 Wt(k)X(k) ≤ 0
    如Xk∈ ω2 且 Wt(k)X(k) ≥ 0。则惩罚：
       W(k+1)=W(k)+f(X)
       直之无惩罚  
 #即要设计一个f(X)随着迭代达到最小

　　确定f(X)的感知器算法的梯度法，是使得f(X)越迭代越小最后收敛为“0”（梯度下降法）
　　设f(X)是向量$X=(x_1,x_2…x_n)$的函数，其梯度向量为

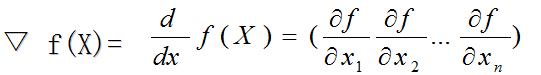
　　它的方向指向自变量(x1,x2…xn)增大时函数f(X)最大增大率方向，反之，负梯度指向f的最陡下降方向。

F.Rosenblett 提出的准则函数
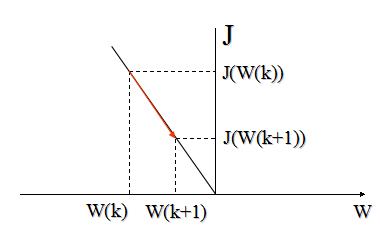
$J(W,X)=C_1(|W_t X|-W_t X)$
$W(k+1)=W(k)-C_2▽ J$ 　 　　　$C_2为有助收敛的校正系数$
这样把求线性不等式组转化为一个使函数J极小化，也就是使$▽J=0$。

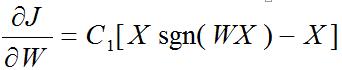
其中

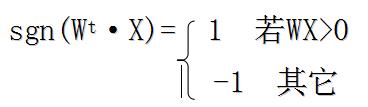
公式表示：

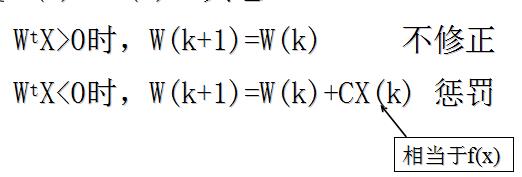
注意

原不等式是对第二类样本的特征向量引如符号后得到的，如不引入负号，则算法为：
如 $X_k∈ω_1 且 W_t(k)X(k) > 0 或$
$X_k∈ω_2 且 W_t(k)X(k) < 0$
则不需要修正 反之，须予以“惩罚”：
若 $X_k∈ω_1 且 W_t(k)X(k) <= 0$
则 $W(k+1)=W(k)+CX(k)$
若 $X_k∈ω_2 且 W_t(k)X(k) >= 0$
则 $W(k+1)=W(k)-CX(k)$

例子

例：有4个训练样本如下：
ω1类： （0，0），（0，1）
ω1类： （1，0），（1，1）
试用感知器算法求其判别函数。

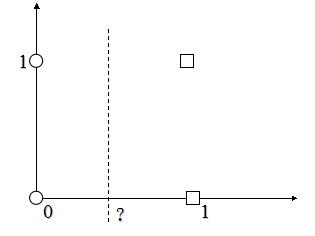
解：特征向量的增1矩阵
$X(1)=(0 0 1)^t, X(2)=(0 1 1)^t$
$X(3)=(1 0 1)^t, X(4)=(1 1 1)^t$
取 C=1,Wt实验一：感知器及其应用

实验一 感知器及其应用

实验一感知器及其应用

实验一

MachineLearning入门-2

K-近邻算法及应用