WPF 画一个3D矩形并旋转
Posted lonelyxmas
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了WPF 画一个3D矩形并旋转相关的知识,希望对你有一定的参考价值。
原文:WPF 画一个3D矩形并旋转
具体的代码还是线性代数。
主要是旋转和平移。
这个例子的中模型是在世界原点建立。所以旋转会以自身轴心旋转。
如果不在世界原点建立模型,还想以自身为旋转轴旋转。
则是需要以下步骤:
模型的中心点为V1(100,100,0)假设中心为轴(平行于Y轴),旋转A度,也就是说自身中心点的Y轴旋转。
步骤:
(1)v1平移到世界原点后其他八个顶点的坐标。(中心点坐标的三个参数如果是大于0就是(每个)顶点减去相对应XYZ,如果中心点坐标的三个参数如果是小于0,则是(每个)顶点加上相对应XYZ,或者使用平移矩阵)
(2)(每个)顶点先是平移到V1在原点时的所在的位置,再使用旋转矩阵经行旋转
(3) (每个)旋转后的顶点在平移回中心点原先所在位置。
ATP 附加属性类
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows; using System.Windows.Controls; using System.Windows.Data; using System.Windows.Media; using System.Windows.Media.Media3D; using System.Windows.Shapes; namespace ATP { public class ATP_Y { public static readonly DependencyProperty P_YProperty = DependencyProperty.RegisterAttached("P_Y", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(0.0, new PropertyChangedCallback(OnP_YChanged))); private static void OnP_YChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { PY = (double)e.NewValue; Draw(d, X, Y, Z); } public static void SetP_Y(DependencyObject d, double v) => d.SetValue(P_YProperty, v); public static double GetP_Y(DependencyObject d) => (double)d.GetValue(P_YProperty); public static readonly DependencyProperty P_XProperty = DependencyProperty.RegisterAttached("P_X", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(0.0, new PropertyChangedCallback(OnP_XChanged))); private static void OnP_XChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { PX= (double)e.NewValue; Draw(d, X, Y, Z); } public static void SetP_X(DependencyObject d, double v) => d.SetValue(P_XProperty, v); public static double GetP_X(DependencyObject d) => (double)d.GetValue(P_XProperty); public static readonly DependencyProperty P_ZProperty = DependencyProperty.RegisterAttached("P_Z", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(0.0, new PropertyChangedCallback(OnP_ZChanged))); private static void OnP_ZChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { PZ = (double)e.NewValue; Draw(d, X, Y, Z); } public static void SetP_Z(DependencyObject d, double v) => d.SetValue(P_ZProperty, v); public static double GetP_Z(DependencyObject d) => (double)d.GetValue(P_ZProperty); public static readonly DependencyProperty ModeDataProperty = DependencyProperty.RegisterAttached("ModeData", typeof(Point3D), typeof(ATP_Y), new PropertyMetadata(new Point3D(10, 10, 10), new PropertyChangedCallback(OnModeDataChanged))); public static void SetModeData(DependencyObject d, Point3D v) => d.SetValue(ModeDataProperty, v); public static Point3D GetModeData(DependencyObject d) => (Point3D)d.GetValue(ModeDataProperty); private static void OnModeDataChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { var data = (Point3D)e.NewValue; ModeWidth = data.X; ModeHeight = data.Y; ModeZWidth = data.Z; Draw(d,X,Y,Z); } public static readonly DependencyProperty YProperty = DependencyProperty.RegisterAttached("Y", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(-1.0, new PropertyChangedCallback(OnYChanged))); public static void SetY(DependencyObject d, double v) => d.SetValue(YProperty, v); public static double GetY(DependencyObject d) => (double)d.GetValue(YProperty); public static readonly DependencyProperty XProperty = DependencyProperty.RegisterAttached("X", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(-1.0, new PropertyChangedCallback(OnXChanged))); private static void OnXChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { var deg = Math.PI / 180 * (double)e.NewValue; X = deg; Draw(d, deg, Y, Z); } public static void SetX(DependencyObject d, double v) => d.SetValue(XProperty, v); public static double GetX(DependencyObject d) => (double)d.GetValue(XProperty); public static readonly DependencyProperty ZProperty = DependencyProperty.RegisterAttached("Z", typeof(double), typeof(ATP.ATP_Y), new PropertyMetadata(-1.0, new PropertyChangedCallback(OnZChanged))); private static void OnZChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { var deg = Math.PI / 180 * (double)e.NewValue; Z = deg; Draw(d, X, Y, deg); } public static void SetZ(DependencyObject d, double v) => d.SetValue(ZProperty, v); public static double GetZ(DependencyObject d) => (double)d.GetValue(ZProperty); private static void OnYChanged(DependencyObject d, DependencyPropertyChangedEventArgs e) { var deg = Math.PI / 180 * (double)e.NewValue; Y = deg; Draw(d, X, deg, Z); } private static double PX, PY, PZ; private static double X, Y, Z; private static double ModeHeight, ModeWidth, ModeZWidth; private static void Draw(DependencyObject d, double X, double Y, double Z) { var ui = d as Grid; ui.Children.Clear(); var rect = new Rect(new Size(ModeWidth,ModeHeight)); Group[0] = new Point3D(rect.Width / 2, rect.Height / 2, -(ModeZWidth/2)); Group[1] = new Point3D(0 - (rect.Width / 2), rect.Height / 2, -(ModeZWidth / 2)); Group[2] = new Point3D(0 - (rect.Width / 2), 0 - (rect.Height / 2), -(ModeZWidth / 2)); Group[3] = new Point3D((rect.Width / 2), 0 - (rect.Height / 2), -(ModeZWidth / 2)); Group[4] = new Point3D(rect.Width / 2, rect.Height / 2, (ModeZWidth / 2)); Group[5] = new Point3D(0 - (rect.Width / 2), rect.Height / 2, (ModeZWidth / 2)); Group[6] = new Point3D(0 - (rect.Width / 2), 0 - (rect.Height / 2), (ModeZWidth / 2)); Group[7] = new Point3D((rect.Width / 2), 0 - (rect.Height / 2), (ModeZWidth / 2)); for (var i = 0; i < 8; i++) PP[i] = PSP(ReturnP3D(Y轴转置矩阵(X, Y, Z) * GetMatrixMP(Group[i])), new Rect(new Size(Math.Max(rect.Height, rect.Width),ModeZWidth))); Set(0, 1, ui,Colors.Black); Set(1, 2, ui,Colors.Blue); Set(2, 3, ui, Colors.Red); Set(3, 0, ui, Colors.Fuchsia); Set(4, 5, ui, Colors.DarkSlateBlue); Set(5, 6, ui, Colors.Red); Set(6, 7, ui, Colors.Red); Set(7, 4, ui, Colors.Red); Set(0, 4, ui, Colors.Red); Set(1, 5, ui, Colors.Red); Set(2, 6, ui, Colors.Red); Set(3, 7, ui, Colors.Red); } private static void Set(int g1, int g2, Grid g,Color A) { var c1 = new Line(); c1.Stroke = new SolidColorBrush(A); c1.X1 = PP[g1].X; c1.Y1 = PP[g1].Y; c1.X2 = PP[g2].X; c1.Y2 = PP[g2].Y; g.Children.Add(c1); } private static Matrix GetMatrixMP(Point3D MP) { var D = new double[4, 1]; D[0, 0] = MP.X; D[1, 0] = MP.Y; D[2, 0] = MP.Z; D[3, 0] = 1; return new Matrix(D); } private static Point3D ReturnP3D(Matrix MP) => new Point3D(MP[0, 0], MP[1, 0], MP[2, 0]); private static Point PSP(Point3D ModePoint, Rect rect) { Point3D vp = new Point3D(PX, PY, Math.Max(rect.Height, rect.Width)+PZ); Point p; int x, y; x = (int)(vp.X + (ModePoint.X - vp.X) * vp.Z / (vp.Z - ModePoint.Z + 0.5)); y = (int)(vp.Y + (ModePoint.Y - vp.Y) * vp.Z / (vp.Z - ModePoint.Z + 0.5)); p = new Point(x, y); return p; } private static Point3D[] Group = new Point3D[8]; private static Point[] PP = new Point[8]; private static Matrix Y轴转置矩阵(double DegX, double DegY, double DegZ) { var A = new double[4, 4]; A[0, 0] = 1; A[0, 1] = 0; A[0, 2] = 0; A[1, 0] = 0; A[1, 1] = Math.Cos(X); A[1, 2] = Math.Sin(X); A[2, 0] = 0; A[2, 1] = 0 - Math.Sin(X); A[2, 2] = Math.Cos(X); A[0, 3] = 0; A[1, 3] = 0; A[2, 3] = 0; A[3, 0] = 1; A[3, 1] = 1; A[3, 2] = 1; A[3, 3] = 1; var B = new double[4, 4]; B[0, 0] = Math.Cos(Y); B[0, 1] = 0; B[0, 2] = -Math.Sin(Y); B[1, 0] = 0; B[1, 1] = 1; B[1, 2] = 0; B[2, 0] = Math.Sin(Y); B[2, 1] = 0; B[2, 2] = Math.Cos(Y); B[0, 3] = 1; B[1, 3] = 1; B[2, 3] = 1; B[3, 0] = 1; B[3, 1] = 1; B[3, 2] = 1; B[3, 3] = 1; var C = new double[4, 4]; C[0, 0] = Math.Cos(Z); C[0, 1] = Math.Sin(Z); C[0, 2] = 0; C[1, 0] = 0 - Math.Sin(Z); C[1, 1] = Math.Cos(Z); C[1, 2] = 0; C[2, 0] = 0; C[2, 1] = 0; C[2, 2] = 1; C[0, 3] = 1; C[1, 3] = 1; C[2, 3] = 1; B[3, 0] = 1; B[3, 1] = 1; B[3, 2] = 1; C[3, 3] = 1; Matrix MT1 = new Matrix(A); Matrix MT2 = new Matrix(B); Matrix MT3 = new Matrix(C); var MT4 = MT1 * MT2; return MT4 * MT3; } } }
xaml代码
//其中ModeData的三个参数为矩形的长高宽
//X,Y,Z为轴的旋转角度
<Window x:Class="ATP.MainWindow" xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation" xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml" xmlns:d="http://schemas.microsoft.com/expression/blend/2008" xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006" xmlns:local="clr-namespace:ATP" mc:Ignorable="d" Title="MainWindow" Height="450" Width="800"> <Grid> <Grid.RowDefinitions> <RowDefinition Height="*"/> <RowDefinition Height="auto"/> </Grid.RowDefinitions> <Grid x:Name="G" local:ATP_Y.P_Z="{Binding ElementName=s4,Path=Value}" local:ATP_Y.ModeData="100,100,100" HorizontalAlignment="Center" VerticalAlignment="Center" local:ATP_Y.Y="{Binding ElementName=s2,Path=Value}" local:ATP_Y.X="{Binding ElementName=s1,Path=Value}" local:ATP_Y.Z="{Binding ElementName=s3,Path=Value}"/> <StackPanel Grid.Row="1"> <!--X轴旋转--> <Slider Minimum="0" Maximum="360" x:Name="s1"/> <!--Y轴旋转--> <Slider Minimum="0" Maximum="360" x:Name="s2"/> <!--Z轴旋转--> <Slider Minimum="0" Maximum="360" x:Name="s3"/> <!--视野远近--> <Slider Minimum="0" Maximum="360" x:Name="s4" /> </StackPanel> </Grid> </Window>
矩阵类
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ATP { [Serializable] public class Matrix { public double[] element; private int rows = 0; private int cols = 0; /// <summary> /// 获取矩阵行数 /// </summary> public int Rows { get { return rows; } } /// <summary> /// 获取矩阵列数 /// </summary> public int Cols { get { return cols; } } /// <summary> /// 获取或设置第i行第j列的元素值 /// </summary> /// <param name="i">第i行</param> /// <param name="j">第j列</param> /// <returns>返回第i行第j列的元素值</returns> public double this[int i, int j] { get { if (i < Rows && j < Cols) { return element[i * cols + j]; } else { throw new Exception("索引越界"); } } set { element[i * cols + j] = value; } } /// <summary> /// 用二维数组初始化Matrix /// </summary> /// <param name="m">二维数组</param> public Matrix(double[][] m) { this.rows = m.GetLength(0); this.cols = m.GetLength(1); int count = 0; this.element = new double[Rows * Cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { element[count++] = m[i][j]; } } } public Matrix(double[,] m) { this.rows = m.GetLength(0); this.cols = m.GetLength(1); this.element = new double[this.rows * this.cols]; int count = 0; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { element[count++] = m[i, j]; } } } public Matrix(List<List<double>> m) { this.rows = m.Count; this.cols = m[0].Count; this.element = new double[Rows * Cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { this[i, j] = m[i][j]; } } } #region 矩阵数学运算 public static Matrix MAbs(Matrix a) { Matrix _thisCopy = a.DeepCopy(); for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { _thisCopy[i, j] = Math.Abs(a[i, j]); } } return _thisCopy; } /// <summary> /// 矩阵相加 /// </summary> /// <param name="a">第一个矩阵,和b矩阵必须同等大小</param> /// <param name="b">第二个矩阵</param> /// <returns>返回矩阵相加后的结果</returns> public static Matrix operator +(Matrix a, Matrix b) { if (a.cols == b.cols && a.rows == b.rows) { double[,] res = new double[a.rows, a.cols]; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { res[i, j] = a[i, j] + b[i, j]; } } return new Matrix(res); } else { throw new Exception("两个矩阵行列不相等"); } } /// <summary> /// 矩阵相减 /// </summary> /// <param name="a">第一个矩阵,和b矩阵必须同等大小</param> /// <param name="b">第二个矩阵</param> /// <returns>返回矩阵相减后的结果</returns> public static Matrix operator -(Matrix a, Matrix b) { if (a.cols == b.cols && a.rows == b.rows) { double[,] res = new double[a.rows, a.cols]; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { res[i, j] = a[i, j] - b[i, j]; } } return new Matrix(res); } else { throw new Exception("两个矩阵行列不相等"); } } /// <summary> /// 对矩阵每个元素取相反数 /// </summary> /// <param name="a">二维矩阵</param> /// <returns>得到矩阵的相反数</returns> public static Matrix operator -(Matrix a) { Matrix res = a; for (int i = 0; i < a.rows; i++) { for (int j = 0; j < a.cols; j++) { res.element[i * a.cols + j] = -res.element[i * a.cols + j]; } } return res; } /// <summary> /// 矩阵相乘 /// </summary> /// <param name="a">第一个矩阵</param> /// <param name="b">第二个矩阵,这个矩阵的行要与第一个矩阵的列相等</param> /// <returns>返回相乘后的一个新的矩阵</returns> public static Matrix operator *(Matrix a, Matrix b) { if (a.cols == b.rows) { double[,] res = new double[a.rows, b.cols]; for (int i = 0; i < a.rows; i++) { for (int j = 0; j < b.cols; j++) { for (int k = 0; k < a.cols; k++) { res[i, j] += a[i, k] * b[k, j]; } } } return new Matrix(res); } else { throw new Exception("两个矩阵行和列不等"); } } /// <summary> /// 矩阵与数相乘 /// </summary> /// <param name="a">第一个矩阵</param> /// <param name="num">一个实数</param> /// <returns>返回相乘后的新的矩阵</returns> public static Matrix operator *(Matrix a, double num) { Matrix res = a; for (int i = 0; i < a.rows; i++) { for (int j = 0; j < a.cols; j++) { res.element[i * a.cols + j] *= num; } } return res; } /// <summary> /// 矩阵转置 /// </summary> /// <returns>返回当前矩阵转置后的新矩阵</returns> public Matrix Transpose() { double[,] res = new double[cols, rows]; { for (int i = 0; i < cols; i++) { for (int j = 0; j < rows; j++) { res[i, j] = this[j, i]; } } } return new Matrix(res); } /// <summary> /// 矩阵求逆 /// </summary> /// <returns>返回求逆后的新的矩阵</returns> public Matrix Inverse() { //最后原始矩阵并不变,所以需要深拷贝一份 Matrix _thisCopy = this.DeepCopy(); if (cols == rows && this.Determinant() != 0) { //初始化一个同等大小的单位阵 Matrix res = _thisCopy.EMatrix(); for (int i = 0; i < rows; i++) { //首先找到第i列的绝对值最大的数,并将该行和第i行互换 int rowMax = i; double max = Math.Abs(_thisCopy[i, i]); for (int j = i; j < rows; j++) { if (Math.Abs(_thisCopy[j, i]) > max) { rowMax = j; max = Math.Abs(_thisCopy[j, i]); } } //将第i行和找到最大数那一行rowMax交换 if (rowMax != i) { _thisCopy.Exchange(i, rowMax); res.Exchange(i, rowMax); } //将第i行做初等行变换,将第一个非0元素化为1 double r = 1.0 / _thisCopy[i, i]; _thisCopy.Exchange(i, -1, r); res.Exchange(i, -1, r); //消元 for (int j = 0; j < rows; j++) { //到本行后跳过 if (j == i) continue; else { r = -_thisCopy[j, i]; _thisCopy.Exchange(i, j, r); res.Exchange(i, j, r); } } } return res; } else { throw new Exception("矩阵不是方阵无法求逆"); } } #region 重载比较运算符 public static bool operator <(Matrix a, Matrix b) { bool issmall = true; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] >= b[i, j]) issmall = false; } } return issmall; } public static bool operator >(Matrix a, Matrix b) { bool issmall = true; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] <= b[i, j]) issmall = false; } } return issmall; } public static bool operator <=(Matrix a, Matrix b) { bool issmall = true; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] > b[i, j]) issmall = false; } } return issmall; } public static bool operator >=(Matrix a, Matrix b) { bool issmall = true; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] < b[i, j]) issmall = false; } } return issmall; } public static bool operator !=(Matrix a, Matrix b) { bool issmall = true; issmall = ReferenceEquals(a, b); if (issmall) return issmall; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] == b[i, j]) issmall = false; } } return issmall; } public static bool operator ==(Matrix a, Matrix b) { bool issmall = true; issmall = ReferenceEquals(a, b); if (issmall) return issmall; for (int i = 0; i < a.Rows; i++) { for (int j = 0; j < a.Cols; j++) { if (a[i, j] != b[i, j]) issmall = false; } } return issmall; } public override bool Equals(object obj) { Matrix b = obj as Matrix; return this == b; } public override int GetHashCode() { return base.GetHashCode(); } #endregion public double Determinant() { if (cols == rows) { Matrix _thisCopy = this.DeepCopy(); //行列式每次交换行,都需要乘以-1 double res = 1; for (int i = 0; i < rows; i++) { //首先找到第i列的绝对值最大的数 int rowMax = i; double max = Math.Abs(_thisCopy[i, i]); for (int j = i; j < rows; j++) { if (Math.Abs(_thisCopy[j, i]) > max) { rowMax = j; max = Math.Abs(_thisCopy[j, i]); } } //将第i行和找到最大数那一行rowMax交换,同时将单位阵做相同初等变换 if (rowMax != i) { _thisCopy.Exchange(i, rowMax); res *= -1; } //消元 for (int j = i + 1; j < rows; j++) { double r = -_thisCopy[j, i] / _thisCopy[i, i]; _thisCopy.Exchange(i, j, r); } } //计算对角线乘积 for (int i = 0; i < rows; i++) { res *= _thisCopy[i, i]; } return res; } else { throw new Exception("不是行列式"); } } #endregion #region 初等变换 /// <summary> /// 初等变换:交换第r1和第r2行 /// </summary> /// <param name="r1">第r1行</param> /// <param name="r2">第r2行</param> /// <returns>返回交换两行后的新的矩阵</returns> public Matrix Exchange(int r1, int r2) { if (Math.Min(r2, r1) >= 0 && Math.Max(r1, r2) < rows) { for (int j = 0; j < cols; j++) { double temp = this[r1, j]; this[r1, j] = this[r2, j]; this[r2, j] = temp; } return this; } else { throw new Exception("超出索引"); } } /// <summary> /// 初等变换:将r1行乘以某个数加到r2行 /// </summary> /// <param name="r1">第r1行乘以num</param> /// <param name="r2">加到第r2行,若第r2行为负,则直接将r1乘以num并返回</param> /// <param name="num">某行放大的倍数</param> /// <returns></returns> public Matrix Exchange(int r1, int r2, double num) { if (Math.Min(r2, r1) >= 0 && Math.Max(r1, r2) < rows) { for (int j = 0; j < cols; j++) { this[r2, j] += this[r1, j] * num; } return this; } else if (r2 < 0) { for (int j = 0; j < cols; j++) { this[r1, j] *= num; } return this; } else { throw new Exception("超出索引"); } } /// <summary> /// 得到一个同等大小的单位矩阵 /// </summary> /// <returns>返回一个同等大小的单位矩阵</returns> public Matrix EMatrix() { if (rows == cols) { double[,] res = new double[rows, cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { if (i == j) res[i, j] = 1; else res[i, j] = 0; } } return new Matrix(res); } else throw new Exception("不是方阵,无法得到单位矩阵"); } #endregion /// <summary> /// 深拷贝,仅仅将值拷贝给一个新的对象 /// </summary> /// <returns>返回深拷贝后的新对象</returns> public Matrix DeepCopy() { double[,] ele = new double[rows, cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { ele[i, j] = this[i, j]; } } return new Matrix(ele); } public override string ToString() { string str = ""; for (int i = 0; i < Rows; i++) { for (int j = 0; j < Cols; j++) { str += this[i, j].ToString(); if (j != Cols - 1) str += " "; else if (i != Rows - 1) str += Environment.NewLine; } } return str; } } }
截图
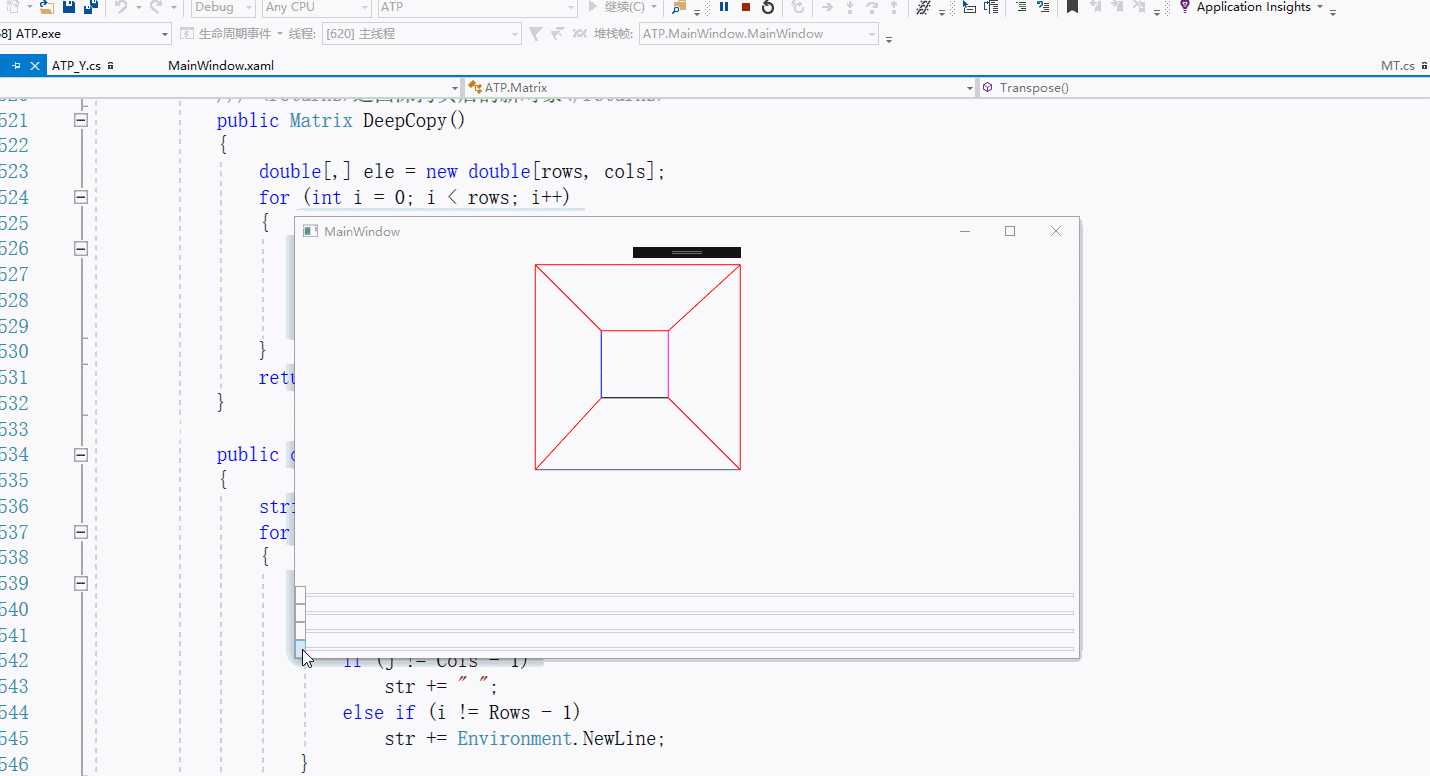
以上是关于WPF 画一个3D矩形并旋转的主要内容,如果未能解决你的问题,请参考以下文章
