Manacher算法 最长回文串

Posted 2020-08-04 每天都不一样

Manacher算法O(n)：主要可以求出以每个字符为中心的最长回文有多长，这个算法有一个很巧妙的地方，它把奇数的回文串和偶数的回文串统一起来考虑了；这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性，避免了大量不必要的重复匹配。

因为对于偶回文，是需要从虚轴扩充，ab，ba，所以如下：

先把原字符串处理，都加上一个标记符，比如#（特殊字符任何都可以，对于计算结果不会有影响）

1221-->#1#2#2#1#

121-->#1#2#1#

按照处理后的字符串求它的最长回文串长度m，所以原始字符串最长子回文串的长度是m／2

 

变量：

1:PArra[] 存放回文半径：某个位置能扩充的回文半径的长度，例如 #1#2#2#1#，2位置PArra[3] = 4

2:int PR 能够扫到的最右的回文的位置   #1#2#1# 在位置3   PR = 6

3:int  index   当 PR更新的时候，index也要更新，指向当前最中心的位置   2中index=3

过程：

当要求位置i的时候的回文半径   分析如下：

1:第一种情况可以直接确定i的回文半径，PR不变，因为没有扩

  

 

 

2:第二种情况，i\'的左边在index左边的左边，PR不用变化，（没有扩）也可以直接确定i位置的回文半径

3:第三种情况，i\'的左边喝index的左边重复，需要从  “右大位置开始继续扩”

如何算复杂度：

如果扩成功了，说明，超过了目前的右大更新PR

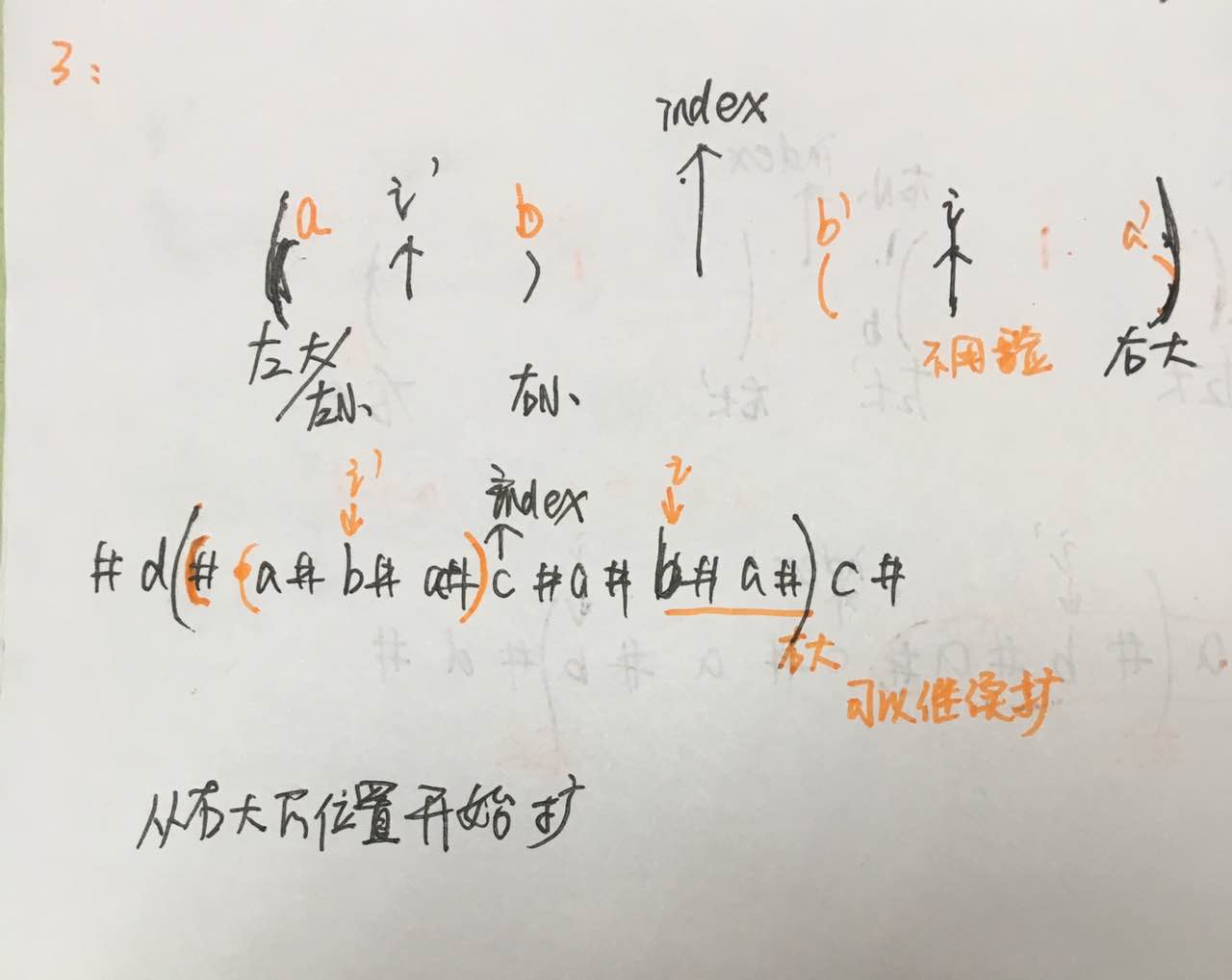
4:第四种情况必须暴力扩

 

 

每一次检查的时候，要么失败，要么成功扩，只要成功扩了，PR必须更新，而且最长扩也就2n，所以“扩”的动作和PR高度相关；

通过变量优化这个算法的时候，一般这个复杂度和这个变量的增量有关。

 http://blog.csdn.net/ggggiqnypgjg/article/details/6645824帮助理解

 http://blog.csdn.net/pi9nc/article/details/9251455