求树上每个节点可以走到的最远距离

Posted 2021-03-02 memset0x3f

1073. 树的中心

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。
请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数，表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤105
输入样例：
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例：
2

第一次DFS求每个节点通过直接点的最远距离max1以及该儿子，并且还需要求一个次远距离max2。然后再求通过父节点可以到达的最远距离max3，可以是合并父节点的max1或max2或max3，但是当父节点的max1的儿子是该节点时，就不能合并，只能尝试合并max2，这就是记录次远距离的作用

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int head[N],cnt,ans;
struct eg{
    int v,c,nex;
}edge[N*2];
int Max1[N],Max2[N],Max3[N];
int son1[N];
void addedge(int u,int v,int c){
    edge[cnt]=(eg){v,c,head[u]};
    head[u]=cnt++;
}
void dfs1(int u,int pre){
    for(int i=head[u];~i;i=edge[i].nex){
        int v=edge[i].v,c=edge[i].c;
        if(pre==v) continue;
        dfs1(v,u);
        if(c+Max1[v]>=Max1[u]){
            Max2[u]=Max1[u];
            Max1[u]=c+Max1[v];
            son1[u]=v;
        }
        else if(c+Max1[v]>Max2[u]){
            Max2[u]=c+Max1[v];
        }
    }
    //cout<<u<<" "<<Max1[u]<<" "<<son1[u]<<"--"<<Max2[u]<<" "<<son2[u]<<endl;
}
void dfs2(int u,int pre){
    for(int i=head[u];~i;i=edge[i].nex){
        int v=edge[i].v,c=edge[i].c;
        if(pre==v) continue;

        if(son1[u]!=v){
            Max3[v]=Max1[u]+c;
        }
        else {
            Max3[v]=Max2[u]+c;
        }
        Max3[v]=max(Max3[u]+c,Max3[v]);
        dfs2(v,u);
    }
}
int main(){
    int n;
    cin>>n;
    memset(head,-1,sizeof head);
    for(int i=1,u,v,c;i<n;++i){
        cin>>u>>v>>c;
        addedge(u,v,c);
        addedge(v,u,c);
    }
    dfs1(1,0);
    dfs2(1,0);
    int ans=1000000000;
    for(int i=1;i<=n;++i)
        ans=min(ans,max(Max1[i],max(Max2[i],Max3[i])));
    cout<<ans<<endl;
    return 0;
}

325. 计算机

一所学校前一段时间买了第一台计算机（所以这台计算机的ID是1）。
近年来，学校又购买了N-1台新计算机。
每台新计算机都与之前买进的计算机中的一台建立连接。
现在请你求出第i台计算机到距离其最远的计算机的电缆长度。

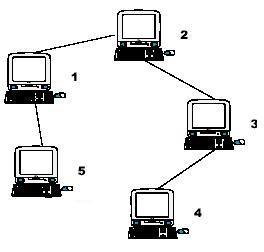
例如，上图中距离计算机1最远的是计算机4，因此 S1=3；距离计算机2最远的是计算机4和5，因此 S2=2；距离计算机3最远的是计算机5，所以 S3=3；同理，我们也得到 S4=4，S5=4。
输入格式
输入包含多测试数据。
每组测试数据第一行包含整数N。
接下来N-1行，每行包含两个整数，第 i 行的第一个整数表示第 i 台电脑买入时连接的电脑编号，第二个整数表示这次连接花费的电缆长度。
输出格式
每组测试数据输出N行。
第i行输出第i台电脑的Si。
数据范围
1≤N≤10000,
电缆总长度不超过109
输入样例：
5
1 1
2 1
3 1
1 1
输出样例：
3
2
3
4
4

带上边权

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int head[N],cnt,ans;
struct eg{
    int v,c,nex;
}edge[N*2];
int Max1[N],Max2[N],Max3[N];
int son1[N],son2[N];
void addedge(int u,int v,int c){
    edge[cnt]=(eg){v,c,head[u]};
    head[u]=cnt++;
}
void dfs1(int u,int pre){
    for(int i=head[u];~i;i=edge[i].nex){
        int v=edge[i].v,c=edge[i].c;
        if(pre==v) continue;
        dfs1(v,u);
        if(c+Max1[v]>=Max1[u]){
            Max2[u]=Max1[u];
            son2[u]=son1[u];
            Max1[u]=c+Max1[v];
            son1[u]=v;
        }
        else if(c+Max1[v]>Max2[u]){
            Max2[u]=c+Max1[v];
            son2[u]=v;
        }
    }
    //cout<<u<<" "<<Max1[u]<<" "<<son1[u]<<"--"<<Max2[u]<<" "<<son2[u]<<endl;
}
void dfs2(int u,int pre){
    for(int i=head[u];~i;i=edge[i].nex){
        int v=edge[i].v,c=edge[i].c;
        if(pre==v) continue;

        if(son1[u]!=v){
            Max3[v]=Max1[u]+c;
        }
        else {
            Max3[v]=Max2[u]+c;
        }
        Max3[v]=max(Max3[u]+c,Max3[v]);
        dfs2(v,u);
    }
}
int main(){
    int n;
    cin>>n;
    memset(head,-1,sizeof head);
    for(int i=2,u,v,c;i<n;++i){
        cin>>u>>v>>c;
        addedge(u,v,c);
        addedge(v,u,c);
    }
    dfs1(1,0);
    dfs2(1,0);
    int ans=1000000000;
    for(int i=1;i<=n;++i)
        ans=min(ans,max(Max1[i],max(Max2[i],Max3[i])));
    cout<<ans<<endl;
    return 0;
}

齐心抗疫

由于最终的答案一定是某个点a被另一个点b帮助，距离a最远的点就一定是b，且b点值一定小于a，如果大于a，那么答案就应该是b点值乘与一个距离大于等于a的距离，答案就会更大。所以只要找到每个点的可以走到的最远距离乘再与他的点值像乘法，就能够找到点a并更新答案

#include<bits/stdc++.h>
using namespace std;
const int N=50010;
int fw[N],h[N],tot,max1[N],max2[N],son1[N],p[N];
struct eg{
    int v,nex;
}e[N*2];
void add(int u,int v){
    e[tot]=(eg){v,h[u]};
    h[u]=tot++;
}
void dfs1(int u,int pre){
    son1[u]=u;
    max1[u]=max2[u]=0;
    for(int i=h[u];~i;i=e[i].nex){
        int v=e[i].v,c=1;
        if(pre==v) continue;
        dfs1(v,u);
        if(max1[v]+c>max1[u]){
            max2[u]=max1[u];
            max1[u]=max1[v]+c;
            son1[u]=son1[v];
        }
        else if(max1[v]+c>max2[u]){
            max2[u]=max1[v]+c;
        }
    }
}
void dfs2(int u,int pre){
    for(int i=h[u];~i;i=e[i].nex){
        int v=e[i].v,c=1;
        if(v==pre) continue;
        fw[v]=0;
        if(son1[u]!=son1[v]&&fw[v]<max1[u]+c){
            fw[v]=max1[u]+c;
        }
        else if(fw[v]<max2[u]+c){
            fw[v]=max2[u]+c;
        }
        if(fw[v]<fw[u]+c){
            fw[v]=fw[u]+c;
        }
        dfs2(v,u);
    }
}
int main(){
    int n;
    memset(h,-1,sizeof h);
    cin>>n;
    for(int i=1;i<=n;++i) cin>>p[i];
    for(int i=2;i<=n;++i){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    dfs1(1,0);
    dfs2(1,0);
    int res=0;
    for(int i=1;i<=n;++i){
        res=max(res,p[i]*max(max1[i],fw[i]));
    }
    cout<<res<<endl;
    return 0;
}