(一)下一个排列
题目(Medium):31. 下一个排列
题目描述:
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
解题思路:
本题有一个比较固定的算法思路,可以总结为以下5步:
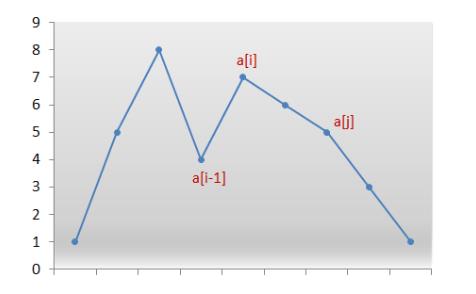
1、从后向前查找第一个相邻升序的元素对 (i,j),满足 A[i] < A[j]。此时 [j,end) 必然是降序
2、在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。则 A[k]是在i之后刚好略大于 A[i]的数。
3、将 A[i] 与 A[k] 交换
4、可以断定这时 [j,end) 必然是降序,逆置 [j,end),使其升序
5、如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
代码实现:
class Solution {
public void nextPermutation(int[] nums) {
//从后往前找到第一个非递增的数字,然后找到其后正好比其大的数字,二者交换,然后将其后的数字反转
//时间复杂度O(n),空间O(1)
int i=nums.length-2;
while(i>=0 && nums[i]>=nums[i+1])
i--;
if(i<0){ //整体是降序的,直接反转
reverse(nums,0,nums.length-1);
return ;
}
//找到i之后刚好大于nums[i]的数字
int j=nums.length-1;
while(j>i && nums[j]<=nums[i])
j--;
swap(nums,i,j);
reverse(nums,i+1,nums.length-1);
}
public void swap(int[] nums,int i,int j){
int temp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
public void reverse(int[] nums,int begin,int end){
int i=begin,j=end;
while(i<j){
swap(nums,i,j);
i++;
j--;
}
}
}
注:可以发现上一篇博文中求下一个更大元素的第三题用的正是这一算法。
(二)全排列
题目(Medium):46. 全排列
题目描述:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
解题思路:回溯 或 交换
方法一:回溯
回溯是一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是 一个解的话(或者至少不是 最后一个解),回溯算法会通过在上一步进行一些变化抛弃该解,即 回溯 并且再次尝试。
这里我们是寻找由数组元素构成的所有排列,实际上相当于寻找所有的解,可以通过回溯来实现。利用递归每次向列表里添加一个数字,数字添加够以后再行回溯,向后添加新的解。
方法二:交换递归
要求所有数组元素构成的排列,可以看成两步:第一步:求所有可能出现在第一个位置的数字,即把第一个字符与后面的数字依次交换。第二步:固定一个数字,求后面所有数字的排列。
很明显,这是典型的递归思路。
两种方法比较,实际上可以发现方法二的效率更高。
代码实现:
//方法一:回溯添加
class Solution {
List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
if(nums==null || nums.length==0)
return res;
backtrack(nums,new ArrayList<>());
return res;
}
public void backtrack(int[] nums,List<Integer> temp){
if(temp.size()==nums.length)
res.add(new ArrayList<>(temp));
else{
for(int num:nums){
if(temp.contains(num))
continue;
temp.add(num);
backtrack(nums,temp); //递归添加下一个
temp.remove(temp.size()-1); //回溯
}
}
}
}
//方法二:交换递归
class Solution {
List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
if(nums==null || nums.length==0)
return res;
permute(nums,0);
return res;
}
public void permute(int[] nums,int begin){
if(begin==nums.length-1){
List<Integer> temp=new ArrayList<>();
for(int num:nums)
temp.add(num);
res.add(temp);
}else{
for(int i=begin;i<nums.length;i++){
swap(nums,begin,i);
permute(nums,begin+1); //后面的递归
swap(nums,begin,i);
}
}
}
public void swap(int[] nums,int i,int j){
int temp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
}
(三)全排列(II)
题目(Medium):47. 全排列 II
题目描述:
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
解题思路:
本题和上一题相比区别在于数组是否包含重复元素,我们可以采用效率较高的交换递归的方法,但是由于可能存在重复,在每次交换时,我们可以通过一个set记录已经交换过的元素,然后再交换时进行判断,如果该元素在set中,就代表已经交换过,没必要再交换,否则就会引起重复记录。
代码实现:
class Solution {
List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
if(nums==null || nums.length==0)
return res;
permuteUnique(nums,0);
return res;
}
public void permuteUnique(int[] nums,int begin){
if(begin==nums.length-1){
List<Integer> temp=new ArrayList<>();
for(int num:nums)
temp.add(num);
res.add(temp);
}else{
Set<Integer> set=new HashSet<>();
for(int i=begin;i<nums.length;i++){
if(set.contains(nums[i])) //已经存在,跳过,不用交换
continue;
set.add(nums[i]);
swap(nums,begin,i);
permuteUnique(nums,begin+1);
swap(nums,begin,i);
}
}
}
public void swap(int[] nums,int i,int j){
int temp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
}
注:求全排列的问题和剑指offer中【剑指Offer】27、字符串的排列 是相同的。
总结:
本文记录了关于排列的三道算法题目,相对来说有一定的难度,特别是求下一个排列和全排列中交换递归的算法思想,可以把其作为一个相对固定的思路理解记忆,同时,我们也看到了回溯和递归思想在其中的应用。