构造二叉树
Posted lz3018
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了构造二叉树相关的知识,希望对你有一定的参考价值。
二叉树是一种特殊的树形结构,每个节点最多有两个子节点,两个节点有左右之分,次序不能颠倒。一般使用递归来定义二叉树,因此与二叉树相关的问题都可以通过递归来解决,二叉树节点的定义如下:

1 class Node{ 2 public int value=-1; 3 public Node leftNode; 4 public Node rightNode; 5 public Node(int val){ 6 value=val; 7 } 8 public Node(){ 9 this(null); 10 } 11 }
接下来介绍根据已知的二叉树结构,构造二叉树的方法。首先给出两个二叉树的结构,如下图所示:

1)根据已有的二叉树结构,生成节点数组,依据节点数组构造二叉树时。约定输入的正数表示其节点编号,负数表示节点不存在。从根节点开始,构造其左子树,如果此树上还有左子树,继续操作,直至没有左子树,然后构造右子树。以A为例说明生成节点数组的过程,设节点数组为nodeArr。首先访问根节点1(nodeArr=[1]),有左子树且根节点为2(nodeArr=[1,2]),以2为根节点继续访问,仍然有左子树且根节点为4(nodeArr=[1,2,4]),继续访问,没有左子树(nodeArr=[1,2,4,-1]),也没有右子树(nodeArr=[1,2,4,-1,-1]),返回到上层,访问2的右子树,且右子树根节点为5(nodeArr=[1,2,4,-1,-1,5]),发现5没有左节点和右节点(nodeArr=[1,2,4,-1,-1,5,-1,-1]),依此类推,最终A的节点数组为nodeArr=[1,2,4,-1,-1,5,-1,-1,3,-1,6,-1,-1]。同理,设B的节点数组为nodeArr2,有nodeArr2=[1,2,4,-1,-1,5,9,-1,-1,-1,3,6,7,-1,8,-1,-1,-1,-1]。
2)根据节点数组,生成二叉树,代码如下:

1 public class traversal { 2 static int step=0; 3 public static void main(String[] args){ 4 int[] nodeArray=new int[]{1,2,4,-1,-1,5,-1,-1,3,-1,6,-1,-1}; 5 int[] nodeArray2=new int[]{1,2,4,-1,-1,5,9,-1,-1,-1,3,6,7,-1,8,-1,-1,-1,-1}; 6 Node root=new Node(); 7 root=createBinaryTree(root,nodeArray2); 8 System.out.println("end"); 9 } 10 public static Node createBinaryTree(Node root,int[] nodeArray ){ 11 int val=-1; 12 try { 13 val = nodeArray[step]; 14 step++; 15 } 16 catch (ArrayIndexOutOfBoundsException ex){ 17 System.out.println("(ArrayIndexOutOfBounds,check the nodeArray"); 18 } 19 if(val<0){ 20 System.out.println("leaf node"); 21 root=null; 22 return root; 23 } 24 root=new Node(val);///指向新对象 25 //step++; 26 root.leftNode=createBinaryTree(root.leftNode,nodeArray); 27 root.rightNode=createBinaryTree(root.rightNode,nodeArray); 28 return root; 29 } 30 } 31 class Node{ 32 public int value=-1; 33 public Node leftNode; 34 public Node rightNode; 35 public Node(int val){ 36 value=val; 37 } 38 public Node(){ 39 } 40 }
3)结果如下所示:

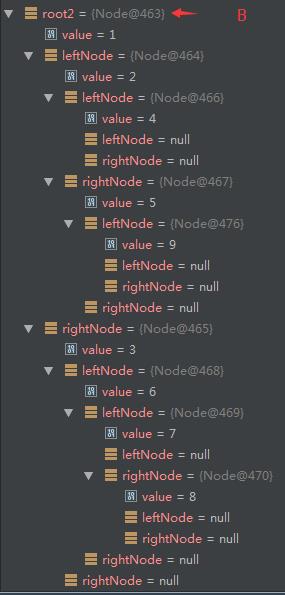
动画演示:http://student.zjzk.cn/course_ware/data_structure/web/flashhtml/erchashujianli.htm
4)事实上,上述构造二叉树的过程是使用了二叉树的先序遍历完成的。在二叉树已经构造完成的基础上,分别完成先序遍历、中序遍历、后序遍历和层次遍历。
先序遍历:先访问根节点,再访问左节点,后访问右节点。如果左节点上还有左子树,继续访问其左节点,然后再访问右节点。
中序遍历:左节点、根节点、右节点。
后序遍历:左节点、右节点、根节点。
层次遍历:首先访问第0层,当i层所有节点访问完之后,再从左向右访问i+1层的各个节点。
使用递归的方法完成先序遍历、中序遍历、后序遍历,使用队列的方法完成层次遍历。代码如下:

1 import java.util.LinkedList; 2 import java.util.Queue; 3 public class traversal { 4 static int step=0; 5 public static void main(String[] args){ 6 int[] nodeArray=new int[]{1,2,4,-1,-1,5,-1,-1,3,-1,6,-1,-1}; 7 int[] nodeArray2=new int[]{1,2,4,-1,-1,5,9,-1,-1,-1,3,6,7,-1,8,-1,-1,-1,-1}; 8 Node root=new Node(); 9 root=createBinaryTree(root,nodeArray); 10 System.out.println("tree A:"); 11 System.out.println("先序遍历:"); 12 nlr(root); 13 System.out.println("\\n" + "中序遍历:"); 14 lnr(root); 15 System.out.println("\\n" + "后序遍历:"); 16 lrn(root); 17 System.out.println("\\n" + "层次遍历:"); 18 levelTraversal(root); 19 Node root2=new Node(); 20 step=0; 21 root2=createBinaryTree(root2,nodeArray2); 22 System.out.println("\\n"+"tree B:"); 23 System.out.println("先序遍历:"); 24 nlr(root2); 25 System.out.println("\\n" + "中序遍历:"); 26 lnr(root2); 27 System.out.println("\\n" + "后序遍历:"); 28 lrn(root2); 29 System.out.println("\\n" + "层次遍历:"); 30 levelTraversal(root2); 31 } 32 public static Node createBinaryTree(Node root,int[] nodeArray ){ 33 int val=-1; 34 try { 35 val = nodeArray[step]; 36 step++; 37 } 38 catch (ArrayIndexOutOfBoundsException ex){ 39 System.out.println("(ArrayIndexOutOfBounds,check the nodeArray"); 40 } 41 if(val<0){ 42 //System.out.println("leaf node"); 43 root=null; 44 return root; 45 } 46 root=new Node(val);///指向新对象 47 //step++; 48 root.leftNode=createBinaryTree(root.leftNode,nodeArray); 49 root.rightNode=createBinaryTree(root.rightNode,nodeArray); 50 return root; 51 } 52 public static void nlr(Node head){ 53 if(head==null){ 54 return; 55 } 56 System.out.print(head.value+"\\t"); 57 nlr(head.leftNode); 58 nlr(head.rightNode); 59 } 60 public static void lnr(Node head){ 61 if(head==null){ 62 return; 63 } 64 lnr(head.leftNode); 65 System.out.print(head.value + "\\t"); 66 lnr(head.rightNode); 67 } 68 public static void lrn(Node head){ 69 if(head==null){ 70 return; 71 } 72 lrn(head.leftNode); 73 lrn(head.rightNode); 74 System.out.print(head.value + "\\t"); 75 } 76 public static void levelTraversal(Node head){ 77 Queue<Node> nodeQueue=new LinkedList<>(); 78 nodeQueue.offer(head); 79 while(!nodeQueue.isEmpty()){ 80 Node node=nodeQueue.poll(); 81 System.out.print(node.value+"\\t"); 82 if (node.leftNode!=null){ 83 nodeQueue.offer(node.leftNode); 84 } 85 if(node.rightNode!=null){ 86 nodeQueue.offer(node.rightNode); 87 } 88 } 89 return; 90 } 91 } 92 class Node{ 93 public int value=-1; 94 public Node leftNode; 95 public Node rightNode; 96 public Node(int val){ 97 value=val; 98 } 99 public Node(){ 100 } 101 }
运行结果图:

三种遍历的非递归实现:

1 //非递归形式的先序遍历 2 public static void nlr2(Node head){ 3 if (head!=null){ 4 return; 5 } 6 Stack<Node> stack=new Stack<>(); 7 stack.push(head); 8 while (!stack.empty()){ 9 Node temp=stack.peek(); 10 System.out.println(temp.value+"\\t"); 11 stack.pop(); 12 if(temp.rightNode!=null){ 13 stack.push(temp.rightNode); 14 } 15 if(temp.leftNode!=null){ 16 stack.push(temp.leftNode); 17 } 18 } 19 20 } 21 22 void lnr2(Node *root)//非递归中序遍历 23 { 24 stack<Node *> stk; 25 Node *p = root; 26 while (p != NULL || !stk.empty()) 27 { 28 if (p != NULL) 29 stk.push(p), p = p->left; 30 else 31 { 32 p = stk.top(); stk.pop(); 33 printf("%d ", p->val); 34 p = p->right; 35 } 36 } 37 } 38 //非递归形式的后序遍历 39 public static void lrn2(Node head){ 40 if(head==null){ 41 return; 42 } 43 Stack<Node> stack1=new Stack<>(); 44 Stack<Node> stack2=new Stack<>(); 45 stack1.push(head); 46 while (!stack1.empty()){ 47 Node tmp=stack1.peek(); 48 stack1.pop(); 49 stack2.push(tmp); 50 if(tmp.leftNode!=null){ 51 stack1.push(tmp.leftNode); 52 } 53 if(tmp.rightNode!=null){ 54 stack1.push(tmp.rightNode); 55 } 56 } 57 while (!stack2.empty()){ 58 System.out.print(stack2.pop().value + "\\t"); 59 } 60 }
参考:http://noalgo.info/832.html
更多代码:

import java.util.*; /** * Created by hfz on 2016/7/5. */ public class traversal { static int step=0; public static void main(String[] args){ int[] nodeArray=new int[]{1,2,4,-1,-1,5,-1,-1,3,-1,6,-1,-1}; int[] nodeArray2=new int[]{1,2,4,-1,-1,5,9,-1,-1,-1,3,6,7,-1,8,-1,-1,-1,-1}; Node root=new Node(); root=createBinaryTree(root,nodeArray); System.out.println("tree A:"); System.out.println("先序遍历:"); nlr(root); System.out.println("\\n" + "非递归先序遍历:"); unRecurNLR(root); nlr2(root); System.out.println("\\n" + "中序遍历:"); lnr(root); System.out.println("\\n" + "非递归中序遍历:"); unRecurLNR2(root); System.out.println("\\n" + "后序遍历:"); lrn(root); System.out.println("\\n" + "层次遍历:"); levelTraversal(root); System.out.printf("%n二叉树叶子节点数量%n%d", getLeafNodeNum(root)); System.out.println("\\n" + "二叉树节点总个数:"); System.out.print(calNodeAmounts(root)); System.out.println("\\n" + "二叉树深度:"); int i=0; System.out.print(calDepth(root, i)); int k=2; System.out.printf("%n第1层到第%d层节点总个数%n",k); System.out.print(calKLevalNodeAmounts(root, k, 1)); System.out.print(String.format("%n第%d层节点个数为%n%d", k, calKthLevel(root, k))); Node root2=new Node(); step=0; root2=createBinaryTree(root2,nodeArray2); System.out.println("\\n"+"tree B:"); System.out.println("先序遍历:"); nlr(root2); System.out.println("\\n" + "非递归先序遍历:"); unRecurNLR(root2); System.out.println("\\n" + "中序遍历:"); lnr(root2); System.out.println("\\n" + "非递归中序遍历:"); unRecurLNR2(root2); System.out.println("\\n" + "后序遍历:"); lrn(root2); System.out.println("\\n" + "层次遍历:"); levelTraversal(root2); System.out.printf("%n二叉树叶子节点数量%n%d", getLeafNodeNum(root2)); System.out.println("\\n" + "二叉树节点个数:"); System.out.print(calNodeAmounts(root2)); System.out.println("\\n" + "二叉树深度:"); System.out.print(calDepth(root2, i)); k=4; System.out.print(String.format("%n第1层到第%d层节点总个数为:%n%d", k, calKLevalNodeAmounts(root2, k, 1))); System.out.print(String.format("%n第%d层节点个数为:%n%d", k, calKthLevel(root2, k))); System.out.printf("%ntree A和tree B 结构是否相同:%n%b",structureCmp(root,root2)); } // 创建二叉树 public static Node createBinaryTree(Node root,int[] nodeArray ){ int val=-1; try { val = nodeArray[step]; step++; } catch (ArrayIndexOutOfBoundsException ex){ System.out.println("(ArrayIndexOutOfBounds,check the nodeArray"); } if(val<0){ //System.out.println("leaf node"); root=null; return root; } root=new Node(val);///指向新对象 //step++; root.leftNode=createBinaryTree(root.leftNode,nodeArray); root.rightNode=createBinaryTree(root.rightNode,nodeArray); return root; } //先序遍历 public static void nlr(Node head){ if(head==null){ return; } System.out.print(head.value+"\\t"); nlr(head.leftNode); nlr(head.rightNode); } //非递归形式的先序遍历 /* 1)申请一个栈来存放节点,首先存入根节点 2)弹出栈顶节点并打印其值,记为cur,将栈顶节点(cur)的右节点(如果有的话)入栈,将栈顶节点(cur)的左节点入栈 3)重复2,直至栈为空 */ public static void unRecurNLR(Node root){ Stack<Node> stack=new Stack<>(); Node cur=root; Node rightNode=null; Node leftNode=null; if(cur==null){ return; } stack.push(cur); while(!stack.empty()){ cur=stack.pop(); System.out.print(cur.value + "\\t"); rightNode=cur.rightNode; leftNode=cur.leftNode; if(rightNode!=null){ stack.push(rightNode); } if(leftNode!=null){ stack.push(leftNode); } } } public static void nlr2(Node head){ Stack<Node> stack=new Stack<>(); ArrayList<Integer> list=new ArrayList<>(); stack.push(head); while (!stack.empty()){ Node temp=stack.peek(); list.add(temp.value); stack.pop(); if(temp.rightNode!=null){ stack.push(temp.rightNode); } if(temp.leftNode!=null){ stack.push(temp.leftNode); } } Integer[] rr=list.toArray(new Integer[]{} ); System.out.println(Arrays.toString(rr)); } //中序遍历 public static void lnr(Node head){ if(head==null){ return; } lnr(head.leftNode); System.out.print(head.value + "\\t"); lnr(head.rightNode); } //非递归形式的中序遍历(自己编写) /* 1)申请栈存放节点,令cur=head 2)将cur指向的节点入栈 3)令cur=cur.leftNode,如果cur!=null,转2,如果栈为空,算法结束,否则弹出cur指向的节点(栈顶节点)node,并打印node 4)弹出栈顶节点后,令cur=node.right,转2 */ public static void unRecurLNR(Node head){ Node cur=head; //Node leftNode=null; //Node rightNode=null; Stack<Node> stack=new Stack<>(); stack.push(cur); while (!stack.empty()){ while (cur!=null) { cur=cur.leftNode; if(cur!=null) stack.push(cur); } cur=stack.pop(); System.out.print(cur.value+"\\t"); cur=cur.rightNode; if(cur!=null) stack.push(cur); } } //非递归形式的中序遍历(书上编写),形式更加简洁。 public static void unRecurLNR2(Node head){ if(head!=null){ Node cur=head; Stack<Node> stack=new Stack<>(); //stack.push(cur); while (!stack.empty()||cur!=null){ if(cur!=null){ stack.push(cur); cur=cur.leftNode; } else{ cur=stack.pop(); System.out.print(cur.value+"\\t"); cur=cur.rightNode; } } } } //后序遍历 public static void lrn(Node head){ if(head==null){ return; } lrn(head.leftNode); lrn(head.rightNode); System.out.print(head.value + "\\t"); } //层次遍历 public static void levelTraversal(Node head){ Queue<Node> nodeQueue=new LinkedList<>(); nodeQueue.offer(head); while(!nodeQueue.isEmpty()){ Node node=nodeQueue.poll(); System.out.print(node.value+"\\t"); if (node.leftNode!=null){ nodeQueue.offer(node.leftNode); } if(node.rightNode!=null){ nodeQueue.offer(node.rightNode); } } return; } //计算二叉树节点总个数 public static int calNodeAmounts(Node head){ if(head==null){ return 0; } return calNodeAmounts(head.leftNode)+calNodeAmounts(head.rightNode)+1; } //计算二叉树深度(自己编写) public static int calDepth(Node head,int counter){ if(head==null){ return counter; } else { counter++; } int a=calDepth(head.leftNode,counter); int b=calDepth(head.rightNode,counter); return a>b?a:b; } //计算二叉树深度(更好实现) public static int calDept2(Node head){ if(head==null){ return 0; } int leftDepth=calDept2(head.leftNode); int rightDepth=calDept2(head.rightNode); return leftDepth>rightDepth?leftDepth+1:rightDepth+1; } //第1层到第k层节点总数量(自己编写) public static int calKLevalNodeAmounts(Node head,int KLevel,int currentLevel){ if(head==null){ return 0; } if(currentLevel<= KLevel){ return calKLevalNodeAmounts(head.leftNode,KLevel,currentLevel+1)+calKLevalNodeAmounts(head.rightNode, KLevel,currentLevel+1)+1; } return 0; } //第k层节点数量 public static int calKthLevel(Node head,int k){ if(hea以上是关于构造二叉树的主要内容,如果未能解决你的问题,请参考以下文章
