究竟谁能赢？——永远在博弈的两个人

Posted 2021-03-11 Y-KnightQin

有一类题目，当你看完题目时，感觉也就那样。

就是两个人，可能一个笨一个精，或者可能两个都非常聪明，然后看谁能赢得比赛。当你觉得这种题目好像很显而易见开始写代码的时候，你写着写着就会被脑子里面的一些奇葩想法所打断。这个人会不会突然搞这出，那个人会不会突然打乱你下一步的操作。然后越想越乱，最后无从下手。

其实，对于这类题目，我一开始是这么想的，既然你都是一场比赛来分胜负，那我是不是可以替你们去玩？我够聪明了吧，我在分饰两角的同时，肯定会找到两个人的套路的。然而现实是我一个人的想法怎么可能分裂出两个人的想法呢？哈哈。于是当我在顾及第一个人的同时，第二个人就对我说你应该操作第一个人这么做，如此反复，做题肯定是做不出来的，没疯倒是不错。这是我之前对博弈题的想法。

当我现在开始研究这类题目，看是否有一个固定的套路的时候，我发现我真的太天真了，要知道博弈论可是运筹学的一个重要学科。什么概念呢？就是知识有一本书那么厚，我想一下子学会是不可能的，而且在竞赛里面不会深究，更多的是看自己的思维，这类题目到最后捋清楚了终将会变得容易。

说了这么多，还是靠刷题来积累经验吧，也算是个十分有效的措施。

 

洛谷P1288

#include <bits/stdc++.h>
#define maxn 5000000
using namespace std;
int n,e[maxn],i,lf,rf;
int main()
{
    cin>>n;
    lf=(maxn<<1);
    rf=-1;
    for (i=1;i<=n;i++) cin>>e[i];
    for (i=1;i<=n;i++) 
        if (!e[i])
        {
            lf=min(lf,i);
            rf=max(rf,i);
        }
    lf--,rf=n-rf;
    if (lf &1 || rf&1)
    {
        printf("YES");
    }
    else
    {
        printf("NO");
    }
    return 0;
}

View Code

这题难度还好，由于题目肯定存在一条0边，所以我们要围绕这条0边来做文章。

我们先把问题简化一下，把题目给的数据看做是一条链。由于一方无路可走意味着另一方胜利，而一次移动最多只能创造出一条0边，这就意味着造成终局的步骤，一定是赢家主动走到了一条0边旁，也就是下图。

 

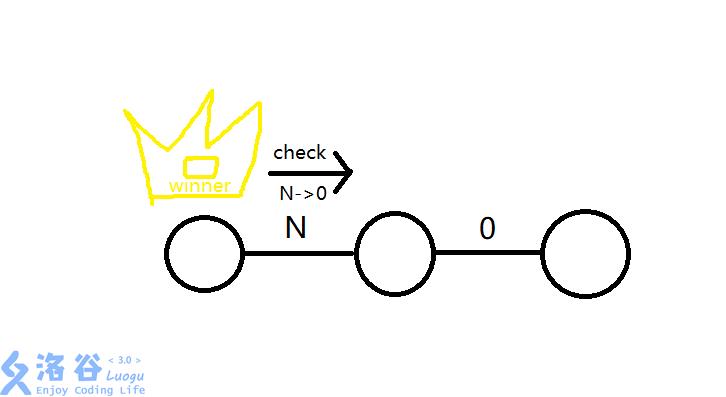
那么得出这个结论有什么用呢？

当一方从起点向0边方向开始行驶，每次把边减为0，即没得回头，两者依次按照这个方法去向0边靠近，当最后一方出现上述情况则赢得比赛。

而这种情况我们可以快速判断出来，即起点离0边的步数为奇数时，肯定能赢。

说到这里，可能会有个问题，为什么我要走的时候一定要把每条边减为0呢？

5种情况。

第一种情况，你在执行这项策略时没有回头路。对手在一次行走中，把第4条边减为0，你把第5条边减为1，那么你就凉了，对手在你走了之后，直接往回走第5条边，这时候你就输了，因为第4 第5 条边都为0。

第二种情况，因为题目终究给的是个环，现在神告诉你在起点的时候，逆时针走你会输，顺时针你会赢。我开始从起点向顺时针走，没有把第1条边减为0，那么到对手走的时候，直接往回走第1条边，此时，你别无选择只能逆时针走，因为第1条边已经减为0，那么你只能输掉比赛。你还不如直接顺时针走，把每条边减为0，别让对手把你往逆时针的方向引。

第三种情况，现在神告诉你在起点的时候，逆时针走你会赢，顺时针你也会赢。我开始从起点向顺时针走，没有把第1条边减为0，那么到对手走的时候，直接往回走第1条边，此时，你别无选择只能逆时针走，因为第1条边已经减为0，。你不觉得很繁琐吗？如果像这样，你还不如直接逆时针走，把边直接减为0，反正你也会赢。

第四种情况，现在神告诉你在起点的时候，逆时针走你会赢，顺时针你会输。情况如第二种情况。

第五种情况，现在神告诉你在起点的时候，你顺逆走怎么都会输，好吧，那我直接把每条边减为0，也不改变结局。

 综上。

因为题目给的是个环，所以我们只要判断究竟逆时针走离0边步数为奇数，还是顺时针离0边步数为奇数，即可得出答案。

 

洛谷P1199

#include <bits/stdc++.h>
using namespace std;
int n,i,j,a[505][505],ans;
int main()
{
    scanf("%d",&n);
    ans=0;
    for (i=1;i<n;i++)
        for (j=i+1;j<=n;j++) 
        {
            scanf("%d",&a[i][j]);
            a[j][i]=a[i][j];
        }
    for (i=1;i<=n;i++)
    {
        sort(a[i]+1,a[i]+1+n);
        ans=(ans>a[i][n-1])?ans:a[i][n-1];    
    }
    printf("1\\n%d\\n",ans);
    return 0;
 } 

View Code

这题较为简单，我们只需找出所有搭配里面第二梯队里面最大的匹配就可以得出答案。

因为机器人比较笨，只会拆散你最大的武将匹配，换句话说就是你永远拿不到最大的武将匹配，你只能拿第二大的武将匹配。

但是会不会存在机器人成精了拿的比我们大呢？答案是不可能的。

我们来分析一下：

第一步，我们要找到所有搭配里面第二梯队里面最大的那个进行匹配，比如把武将①拿走，机器人拿走与其最大的武将匹配的那个武将②。

第二步，我们要找到与武将①搭配里面第二梯队里面最大的那个武将③，把武将③拿走，机器人拿走与其最大的武将匹配的那个武将④。

我们这时候要注意到的是武将②和武将④不会比武将①和武将③的匹配值大，原因：武将②要和武将①搭配才能发挥最大匹配，换言之，武将②和武将④的搭配只能是第二梯队甚至更差，由于武将①和武将③是第二梯队最好的，所以武将②和武将④不会比武将①和武将③的匹配值大。

第三步，我们要当搅屎棍，我们不能保证武将④可能和其他没有被选到的武将会成为最佳匹配，这时候，我们只要和机器人对着选，别让机器人拿到第一梯队的组合就行了，因为我们永远是快了机器人一步。

 

洛谷P1290

#include <bits/stdc++.h>
using namespace std;
int t,n,m;
bool solve(int n,int m,int op)
{
    if (n>=2*m || n==m) return op;
    else
    {
        return(solve(m,n-m,op^1));
    }
}
int main()
{
    cin>>t;
    while (t--)
    {
        cin>>n>>m;
        if (n<m) swap(n,m);
        if (solve(n,m,1)) printf("Stan wins\\n");
            else printf("Ollie wins\\n");
    }
    return 0;
 } 

View Code

这题有点玄学，我不能保证我的想法都适用于这类题目。

由于给的数据有两种情况，

一种是n>2*m的情况，另一种是n<=2*m。

对于第一种情况而言，我们假设一个例子，3*m>n>2*m，先手的人就有掌控权，你可以先将n-m，也可将n-2*m，对于n-m，对手只能（n-m）-m；而对于n-2*m，对手可以m-（n-2*m），也有可能（n-2*m）比较小，可以m-（n-2*m）*2，一旦有种情况导致先手的人输了，那就GG，但是，这种情况的发生，取决于你在做出将n-m，或者将n-2*m的这个决定之后的，你可以回到过去来改变这次决定，比如刚刚对手做出第二轮选择中的m-（n-2*m）*2才赢的，我们是否来取代他，做出这个选择呢？就是说如果我们第一轮将n-2*m，第二轮对手就做出m-（n-2*m）*2赢得比赛。如果我们第一轮将n-m，第二轮对手只能（n-m）-m，第三轮我们就可以替代对手做出m-（n-2*m）*2赢得比赛。综上所诉，一旦出现n>2*m的情况，看谁先手，谁就能赢。

对于第二种情况，就要互相减，直到出现n>2*m的情况，因为在此之前，谁都没有主动权。

这个题目我的想法是，如果我们在一个决定里面有不同的方向，我们是不是必赢？这个我无从考证。

 

洛谷P2148

#include <bits/stdc++.h>
using namespace std;
int t,n,a[20005],ans,i;
int SG(int x,int y)
{
    int a=x,b=y,ass=0;
    while (1)
    {
        if (a &1 && b&1) return ass;
        if (a&1) a++;
        if (b&1) b++;
        a>>=1;b>>=1;ass++;
    }
}
int main()
{
    cin>>t;
    while (t--)
    {
        cin>>n;
        for (i=1;i<=n;i++) scanf("%d",&a[i]);
        ans=0;
        for (i=1;i<=n;i+=2)
        {
            ans^=SG(a[i],a[i+1]);
        }
        if (!ans) printf("NO\\n");
            else printf("YES\\n");
    }
    return 0;
 } 

View Code

首先做这题之前，要对SG函数有概念，为此我花了近一天的时间来看懂这个东西以及几种解决这类题目的方法。

然后我发现，打表是大家公认的高效解题方法，毕竟证明什么的太枯燥难懂，于是我又去看了看别人的打表代码，以及看到一张张截图，我不清楚别人是花多长时间去看那个SG函数表的，我只能说能在一大堆数字里面找出来规律属实是有点厉害。这题证明过程洛谷第一个题解就是，但是我看不太懂，其他的基本都是打表找规律。

 

洛谷P1247

#include <bits/stdc++.h>
#define maxn 500010
using namespace std;
int n,a[maxn],i,j,ans;
int main()
{
    cin>>n;
    ans=0;
    for (i=1;i<=n;i++) 
    {
        cin>>a[i];
        ans^=a[i];
    }
    if (!ans) printf("lose\\n");
    else
    {
        for (i=1;i<=n;i++)
        {
            if ((ans^a[i])<a[i])
            {
                printf("%d %d\\n",a[i]-(ans^a[i]),i);
                for (j=1;j<=n;j++)
                    if (j!=i) printf("%d ",a[j]);
                        else printf("%d ",ans^a[i]);
                break;
            }
        }
    }
    return 0;
}

View Code

这题有所变通，在解决第一问时，只需全部异或一下就可得出答案。

如果必胜，那么我们来解决第二问。

我们设第一问是a1^a2^a3^……^an=X

那么我们可以左右两边同时异或X。a1^a2^a3^……^an^X=X^X 得到 a1^a2^a3^……^an^X=0

又因为交换律 我们可以依次将X与a进行组合，比如 a1^（a2^X）^a3^……^an=0

我们这么做有什么用呢？先手必胜，即先手可以拿走一些火柴，使得后手必败，而必败态是火柴堆的异或和为零；那么我们求的，就是先手拿走一些火柴后，新的火柴堆异或和为零的方案。

如果发现（a?^X）<  a？那么我们根据题目要求，我们可以指定这一堆是拿了之后的状态，得到答案。