做一道 初三题

Posted 2021-03-14 凯特琳

在 数学吧 里 有 一个 帖 《万能的吧友，救救这名卑微的初三狗吧》   http://tieba.baidu.com/p/6455416605   ，   里面 提问 了一个 题 ，  如下 ：

 

 

 

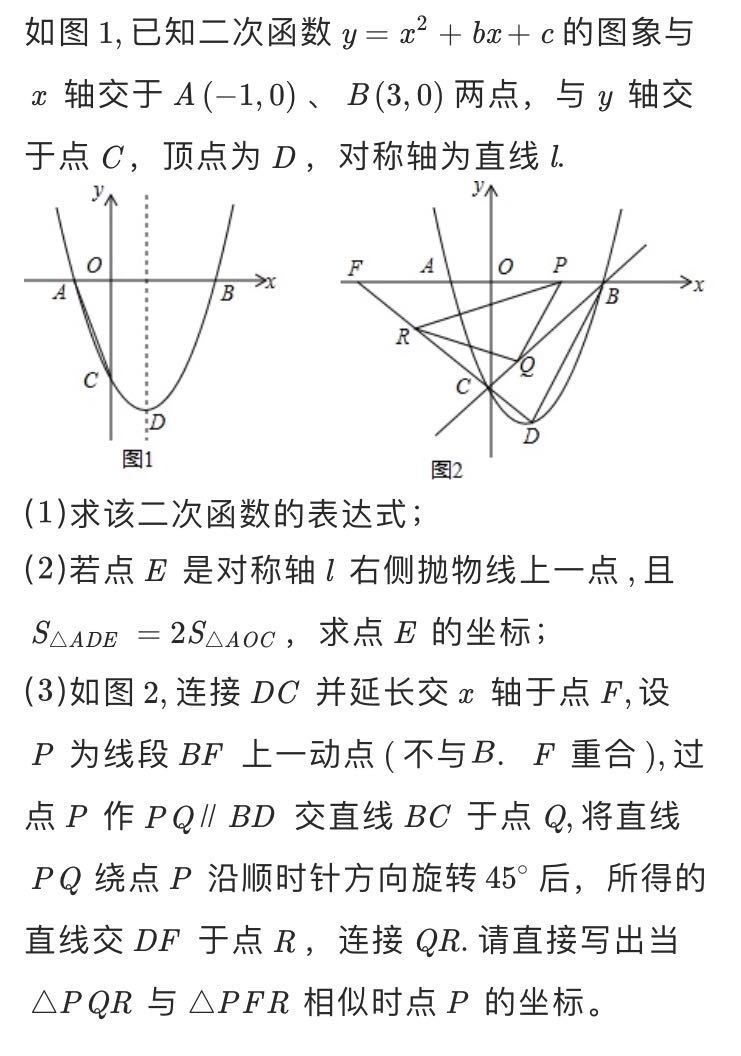
我们 来 做做 这道题，   

 

（1）   函数图像 与 x 轴 相交于  A (-1, 0) 、 B (3, 0)   两点，  可以列 方程组 ：

 

0 =  ( -1 ) ² + b * -1 + c

0 = 3 ² + b * 3 + c

 

1 - b = 9 + 3 b

4 b = - 8

b = -2

 

c = -9 - 3 * -2 = -9 + 6 =  -3

 

所以，  函数表达式 是   y = x ² - 2x - 3     。

 

（2）   过 E 点 作 高 与 AD 相交于 H 点，  即  EH 是 过 E 点 的 高， 

 

因为  EH 和 抛物线 右侧 相交于 点 E，  所以， ye = xe ² - 2xe - 3   ，   xe ye 是 E 点 的 x y 坐标  ，  xe > 1    。

 

根据  S△ADE = 2 S△AOC   ，       可以 列方程 ：          1/2 * AD * EH  =   2 *  1/2 * Xa * Yc    ，    Xa 是 A 点 x 坐标，  Yc 是 C 点 y 坐标  ，

1/2 * AD * EH = Xa * Yc

EH = 2 * Xa * Yc / AD          （1） 式

 

Xa = -1，    另外，  可以知道  Xd = 1 ，   Xd 是 D 点 x 坐标，    Yd = Xd ² - 2Xd - 3   = 1 ² - 2 * 1 - 3 = -4  ， Yd 是 D 点 y 坐标     。

 

根据 勾股定理 ，    AD = ( Yd ² + ( Xd - Xa ) ² ) 开方 = ( 4 ² + 2 ² ) 开方 = 根号 ( 20 )      。

 

又因为 Yc = Xc ² - 2Xc - 3 = 0 ² - 2 * 0 - 3 = -3，    Xc Yc 是 C 点 的 x y 坐标   。

 

代入 （1） 式  ，     EH = 2 * Xa * Yc / AD = 2 * -1 * -3 / 根号 ( 20 )  =   6 / 根号 ( 20 )     。

 

 

 

图中 蓝色 的 字 和 辅助线 是 我 加 的   。            如图，   可以知道，  三角形 ADG 和 EFH 相似，  ∠ ADG = ∠ FEH  ，  

cos ∠ FEH = cos ∠ ADG = DG / AD = 4 / 根号 ( 20 )    ，

 

EH / EF = cos ∠ FEH =  4 / 根号 ( 20 )   

EF = EH * 根号 ( 20 )  / 4 =  6 / 根号 ( 20 )  * 根号 ( 20 )  / 4 = 6 / 4 = 3 / 2  

 

另外，   可以知道  AD 直线 的 函数式 是   y = -2x - 2    ，

 

因为 EF 平行于 x 轴，   和  AD 交于 F，  和 抛物线 交于 E，    可以 列方程组 ：

 

-2x1 - 2 = x2 ² - 2x2 - 3     ，    x1 表示 直线 AD  y = -2x - 2   的 x，   x2 表示 抛物线 的   y = x ² - 2x - 3  的 x，

x2 - x1 = EF = 3/2

 

解方程组 ：

x1 = x2 - 3/2

 

-2 ( x2 - 3/2 ) - 2 = x2 ² - 2x2 - 3  

-2 x2 + 3 - 2 = x2 ² - 2x2 - 3  

x2 ² = 4

x2 = 2

 

x2  就是 E 点 的 x 坐标，  代入 抛物线 函数式    y = x ² - 2x - 3   ，  

y = 2 ² - 2 * 2 - 3 = -3   

 

y 就是 E 点 的 y 坐标，  所以 E 点 的 坐标 是  x = 2, y = -3   。

 

（3）    先求 DC 直线 函数式，   设 函数式 为    y = ax + b ，   根据 C 点 D 点 坐标 来 求 函数式   。

 

 

 

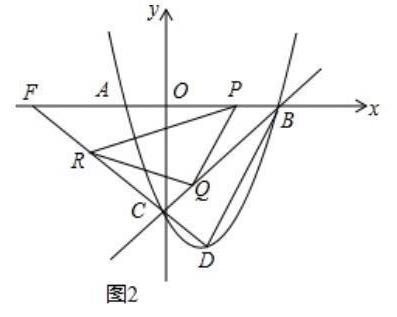
可以知道， C 点 y 坐标 y = x ² - 2x - 3 = 0 ² - 2 * 0 -3 = -3  ，   D 点 x 坐标 为 1，  y = x ² - 2x - 3 = 1 ² - 2 * 1 - 3 = -4  ，

所以， C 点 坐标 是 ( 0, -3 )，  D 点 坐标 是  ( 1, -4 )     ，

 

-3 = a * 0 + b

-4 = a * 1 + b

 

a =   -1

 

a =  -1   表示 三角形 FCO 是 等腰直角三角形，   ∠ OFC = 45 度  ，    因为 ∠ RPQ = 45 度，  所以 ∠ OFC = ∠ RPQ  ，

所以，  要 使  三角形 PQR 和 PFR 相似， 只要 让 RQ 直线 平行于  x 轴 就可以了，   此时，  ∠ FPR = ∠ PRQ ，  所以   三角形 PQR 和 PFR 相似   。

所以，  只要  求  RQ 直线 和 x 轴 平行 时  P 的 坐标 就可以了   。

 

 

 

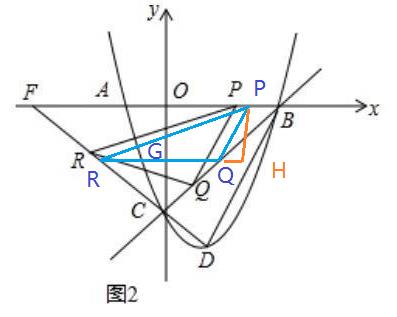
用 蓝色 的 线条 和 字  标识 出 实际 满足条件 的 P R Q ，   并 用 橙色 线条 作 延长线 QH PH 正交于 H   。

 

根据 B 点 坐标 ( 3 0 ) 和 D 点坐标 ( 1, -4 )   可以 知道 BD 直线 的 斜率 = 4/2 = 2     。 

所以 tan ∠ QPH = 1/2 ，  因为 ∠ RPQ = 45 度，  所以，  ∠ RPH = ∠ QPH + ∠ RPQ = arctan 1/2 + 45 度     。

 

RH / PH = tan ∠ RPH = tan ( arctan 1/2 + 45 度 ) 

RH = PH * tan ( arctan 1/2 + 45 度 ) 

RG + GQ + QH = PH * tan ( arctan 1/2 + 45 度 ) 

 

因为 等腰直角三角形，  所以 RG  = GQ  ， 

2 RG + QH = PH * tan ( arctan 1/2 + 45 度 ) 

 

因为 QH / PH = tan ∠ QPH = 1/2 ， 所以   QH = 1/2 PH ， 

2 RG + 1/2 PH = PH * tan ( arctan 1/2 + 45 度 )       (1) 式

 

因为 CG =  OC - PH，   因为 等腰直角三角形 ，    RG = CG = OC - PH，    因为 等腰直角三角形 ，   OC = OB  ，  因为  B 的 坐标 是  ( 3 ,  0 )  ，    所以 OC = OB =  3  ，

所以      RG = OC - PH = 3 - PH ，  代入  (1) 式

 

2 ( 3 - PH ) + 1/2 PH = PH *  tan ( arctan 1/2 + 45 度 ) 

6 - 2 PH + 1/2 PH = PH *  tan ( arctan 1/2 + 45 度 ) 

PH *  tan ( arctan 1/2 + 45 度 )  + 3/2 PH = 6

PH ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) = 6

PH = 6 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) 

 

RH = PH * tan ( arctan 1/2 + 45 度 ) = 6 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 ) 

QH = 1/2 PH = 1/2 * 6 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) = 3 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) 

 

2 RG+ QH = RH

2 RG + 3 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  =  6 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 ) 

RG =  [ 6 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 )  - 3 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) ] / 2

= 3 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 )  -   3/2 * 1 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 )

 

GH = GQ + QH ，    因为  GQ = RG，   所以

GH = RG + QH 

=  3 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 )  -   3/2 * 1 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) + 3 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) 

 

P 点 的 x 坐标 就是 GH，  即 P 点 的 x 坐标 是 3 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 )  * tan ( arctan 1/2 + 45 度 )  -   3/2 * 1 / ( tan ( arctan 1/2 + 45 度 )  + 3/2 ) + 3 /  ( tan ( arctan 1/2 + 45 度 )  + 3/2 )       。

 

 

这道题 要 做完 全部  3 小题 ，  就算 不假思索 的 做，  也要 做 半个小时，   一场 考试  2 个小时 ，  做 4 题 就 差不多 了 ，  呵呵   。

 

所以，   高分 是 训练 出来 的，   这就像 竞技比赛 里  专业选手 和 业余选手 的 差别，    比如 星际争霸，   职业选手 和 业余选手 的 差距 是 巨大 的  。