软件工程基础个人个人项目 数独终局声称与解数独问题的控制台程序

Posted 2020-11-24 yzqiangblog

Github项目

https://github.com/YZqiangGithub/SolveSudokuPromblem

时间预估：

 

 

 

 

 需求分析：

　　从项目的描述来看，项目的需求比较单一，通过命令行参数来控制当前输出要求数量的数独的终局还是给出前所给文件路径下的数独问题的一个可行解。

 

模块划分：

• 命令行参数类型和合法判断还有参数处理

　　从命令行得到命令行参数后，先判断命令行给出的命令类型，是输出要求数量的终局还是解一个数独问题，接着判断下一个参数的合法性，如要求生成的终局数是否为一个1~1e6的整数。以上检查完毕则调用相应的模块。

• 生成数独终局

　　生成命令行中输入的指定数量的终局，并按照指定的格式输入文件suduku.txt。

• 解决数独问题

　　从指定的路径中的到需要解决的数度问题，一个可行解按照要求的格式输入到文件sudoku.txt。

功能建模 ：

　　通过数据流图来进行功能建模。

　　顶层图：

　　　　

 

 

 　　第一层图：

 

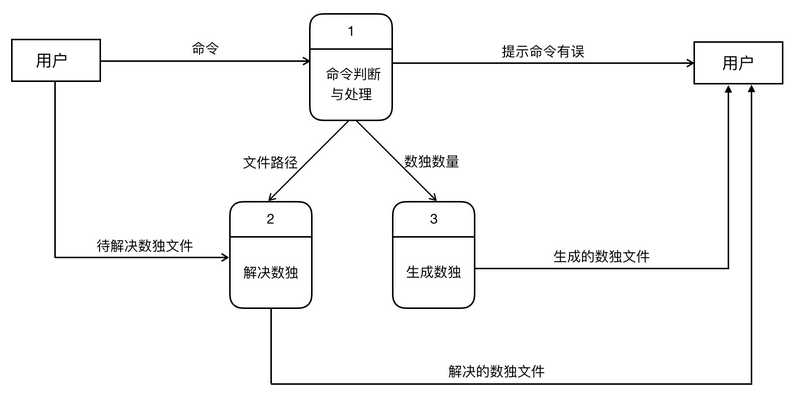
 行为建模：

　　状态转换图：

　　　　

 

 

 

 

 

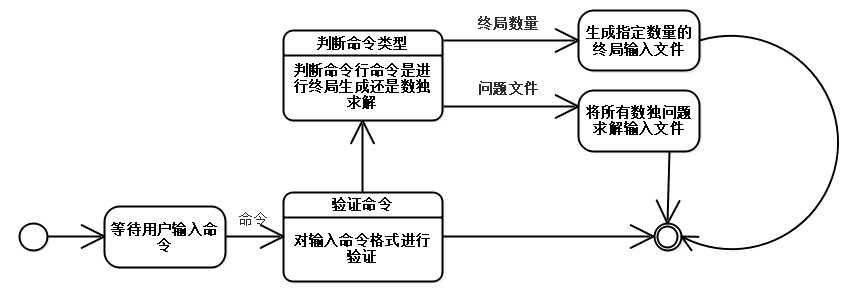
解题思路：

　生成终局算法思路：

　　我在一开始是想通过随机的办法来解决生成不同的解，但是每一次生成的终局都要将前面的计算过程全部走一遍，效率太低，所以我就参考了xxrxxr的博客， 以一个已有的终局为模板，通过以下的两种方式生成剩下的终局：

　　1.数字的交换

　　　　因为当前的终局已经满足数独条件，且数字的交换并不会破坏数字间的位置关系，因此可以通过数字的交换来生成其他终局。
　　　　第 1 行第 1 个数字固定为学号末两位模 9 加 1 ，因此只能交换剩下 8 个数字，可以生成8! = 40,320种终局

　　2.行的交换

　　　数独终局 1-3、4-6、7-9 行之间可以交换，且不破坏数独条件，因此可以通过行的交换生成其　　他终局。
　　   第 1 行第 1 个数字固定为学号末两位模 9 加 1 ，因此只能交换 2-3、4-6、7-9行，可以生成2! * 3! * 3! = 72种终局

　　两种方式相结合将有8! * 2! * 3! * 3! = 2,903,040 种终局，大于所要求的1e6。

　  求解数独思路：

 

　　　　求解的主要思路设计参考了暴力算法之美：如何在1毫秒内解决数独问题？| 暴力枚举法+深度优先搜索 POJ 2982，即通过暴力枚举和深度优先搜索，但是采用的这两种办法所消耗的计算较大，求解的数独数目最高可达到1000000个，且空白的数目很多，因此需要对算法进行优化。

　　　　优化算法主要通过将数独中的空白按照可选填数字由大到小的顺序进行排序，因此每个空白格可选填的数字个数就是（9 - max(所在行已填入数字个数，所在列已填入数字个数))。

　　　　更加精准的优化方式即通过每个 3 x 3 的小宫格来优化，优化后每个空白格填入的数字个数就为（9- max(所在行已填入数字的格数，所在列已填入数字的格子的格数，所在3 x 3 的小宫格已填入数字的格数)）。